In the above example, if temperature of inner surface P is kept constant at θ1 and of the outer surface Q at θ2(<θ1). Then,
Find.
(a) rate of heat flow or heat current from inner surface to outer surface.
(b) temperature θ at a distance r(a<r<b) from centre.
The correct Answer is:A, B, D
To solve the problem step by step, we will break it down into two parts: (a) calculating the rate of heat flow (heat current) from the inner surface to the outer surface, and (b) determining the temperature at a distance r from the center.
Part (a): Rate of Heat Flow (Heat Current)
1. Identify the temperatures: We have the inner surface temperature θ1 and the outer surface temperature θ2 where θ1>θ2.
2. Calculate the temperature difference: The temperature difference ΔT is given by:
ΔT=θ1−θ2
3. Determine the thermal resistance: The thermal resistance R for a spherical shell can be calculated using the formula:
R=14πk(1a−1b)
where k is the thermal conductivity, a is the radius of the inner surface, and b is the radius of the outer surface.
4. Use the formula for heat current: The rate of heat flow (heat current H) can be calculated using:
H=ΔTR
Substituting the expression for R:
H=ΔT⋅4πk(1a−1b)
5. Substitute ΔT:
H=(θ1−θ2)⋅4πk(1a−1b)
Part (b): Temperature θ at a distance r from the center
1. Assume a temperature at distance r: Let the temperature at a distance r from the center be θ.
2. Write the heat current equations: The heat current flowing into point A (at distance r) and out of point A can be expressed as:
H1=θ−θ2R1andH2=θ1−θR2
where R1=14πk(1r−1a) and R2=14πk(1b−1r).
3. Set the net heat current to zero: Since there is no heat source at point A, the heat currents must balance:
H1−H2=0⇒H1=H2
4. Substituting the expressions for H1 and H2:
θ−θ214πk(1r−1a)=θ1−θ14πk(1b−1r)
5. Cross-multiply and simplify:
(θ−θ2)(1b−1r)=(θ1−θ)(1r−1a)
6. Rearranging terms: After simplifying, you can express θ in terms of θ1, θ2, a, b, and r.
Final Result
- The rate of heat flow from the inner surface to the outer surface is:
H=(θ1−θ2)⋅4πk(1a−1b)
- The temperature θ at a distance r from the center can be expressed as:
θ=B⋅A−R⋅θ2+A⋅(B−R)⋅θ1AB−BR+AB−AR
ΔT=θ1−θ2
R=14πk(1a−1b)
where k is the thermal conductivity, a is the radius of the inner surface, and b is the radius of the outer surface.
H=ΔTR
Substituting the expression for R:
H=ΔT⋅4πk(1a−1b)
H=(θ1−θ2)⋅4πk(1a−1b)
H1=θ−θ2R1andH2=θ1−θR2
where R1=14πk(1r−1a) and R2=14πk(1b−1r).
H1−H2=0⇒H1=H2
θ−θ214πk(1r−1a)=θ1−θ14πk(1b−1r)
(θ−θ2)(1b−1r)=(θ1−θ)(1r−1a)
H=(θ1−θ2)⋅4πk(1a−1b)
θ=B⋅A−R⋅θ2+A⋅(B−R)⋅θ1AB−BR+AB−AR
Topper's Solved these Questions
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 2
2 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Example Type 3
1 Video
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- BASIC MATHEMATICSBOOK - DC PANDEY ENGLISHCHAPTER - BASIC MATHEMATICSEXERCISE - Exercise
13 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEY ENGLISHCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Medical entrance s gallery
38 Videos
Similar Questions
The ends of a metal rod are kept at temperatures θ1 and θ2 with θ2>θ1. The rate of flow of heat along the rod is directly proportional to
View SolutionThe ends of a metal rod are kept at temperature θ1andθ2 with θ2>θ1. At steady state the rate of flow of heat along the rod is directly proportional to
View SolutionA hollow metal sphere of radius 5 cm is charged such that the potential on its surface is 10 V. The potential at the centre of the sphere is
View SolutionA charge Q is placed at the centre of an uncharged, hollow metallic sphere of radius a. (a) Find the surface charge density on the inner surface and on the outer surface. (b) If a charge q is put on the sphere, what would be the surface charge densities on the inner and the outer surface? (c) Find the electric field inside the sphere at a distance x from the centre in the situations (a) and (b).
View SolutionA hollow spherical conductor of radius r potential of 100 V at its outer surface. The potential inside the hollow at a distance ofr2 from its centre is
View SolutionA small conducting spherical shell with inner radius a and outer radius b is concentric with a larger conducting spherical shell with inner radius c and outer radius d. The inner shell has total charge +2q and the outer shell has charge +4q.
(i) What is the total charge on the (a) inner surface of the small shell, (b) outer surface of the small shell (c) inner surface of the large shell, (d) outer surface of the large shell ?
(ii) Calculate the electric field in terms of q and the the distance r from the common centre of two shells for (a) r<a, (b) a<r<b, (c) b<r<c, (d) c<r<d, (e) r>d

View SolutionTwo liquids of specific heat ratio 1:2 are at temperature 2θandθ
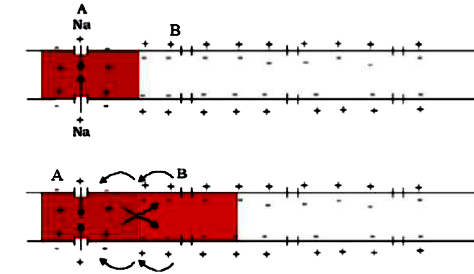
View SolutionWhich of the following helps in current flow on the inner surface of an axon from site-A to site-B as shown in the figure given below ?
View SolutionThe solar constant for a planet is S. The surface temperature of the sun is TK. The sun subtends an angle θ at the planet:
View SolutionWe have a disc of neglligible thickness and whose surface mass density varies as radial distance from centre as σ=σ0(1+rR), where R is the radius of the disc. Specific heat of the material of the disc isC.
Disc is given an angular velocity ω0 and placed on a horizontal rough surface such that the plane of the disc is parallel to the surface. Coefficient of friction between disc and suface is μ. The temperature of the disc is T0.
Answer the following question on the base of information provided in the above paragraph
If the kinetic energy lost due to the friction between disc and surface is absorbed by the disc the moment heat is generated, by the mass lying at the point where the energy is lost. Assume that there is no radial heat flow in betwen disc particles. Rate of change in temperature at a point lying at r distance away from centre with time, before disc stops rotating, will be (α-magnitude of angular acceleration of rod)
View Solution
