In the above problem. The plane of the coil is initially kept parallel to B. The coil is rotated by an angle θ about the diameter perpendicular to B and charge of amount Q flows through it. Choose the correct alternatives.
(a) θ=90∘,Q=(Ban/R)
(b) θ=180∘,Q=(Ban/R)
( c) θ=180∘,Q=0
( d) θ=360∘,Q=0
The correct Answer is:A, C, D
To solve the problem, we need to determine the amount of charge Q that flows through the coil when it is rotated by an angle θ about a diameter perpendicular to the magnetic field B. We will follow these steps:
Step 1: Understand the Initial Conditions
Initially, the plane of the coil is parallel to the magnetic field B. The area vector →A of the coil is also parallel to B. Therefore, the initial angle θi=0∘.
Step 2: Determine the Magnetic Flux
The magnetic flux Φ through the coil is given by:
Φ=B⋅A⋅cos(θ)
Where:
- B is the magnetic field strength,
- A is the area of the coil,
- θ is the angle between the area vector and the magnetic field.
Initially, when the coil is parallel to B:
Φi=B⋅A⋅cos(0)=B⋅A
Step 3: Calculate the Final Flux After Rotation
After rotating the coil by an angle θ, the new angle θf becomes θ. Thus, the final magnetic flux is:
Φf=B⋅A⋅cos(θ)
Step 4: Calculate the Change in Flux
The change in magnetic flux ΔΦ is given by:
ΔΦ=Φf−Φi=B⋅A⋅cos(θ)−B⋅A=B⋅A(cos(θ)−1)
Step 5: Calculate the Induced EMF
According to Faraday's law of electromagnetic induction, the induced EMF E in the coil is given by:
E=−dΦdt
For a finite change, we can express it as:
E=−nΔΦΔt
Where n is the number of turns in the coil.
Step 6: Relate EMF to Current
Using Ohm's law, the current I flowing through the coil can be expressed as:
I=ER
Where R is the resistance of the coil.
Step 7: Calculate the Charge Flowing Through the Coil
The charge Q that flows through the coil can be calculated using the relationship:
Q=I⋅t
Substituting for I:
Q=ER⋅t
Substituting for E:
Q=−nR⋅ΔΦ
Substituting for ΔΦ:
Q=−nR⋅B⋅A(cos(θ)−1)⋅t
Step 8: Analyze Specific Cases
1. When θ=0∘:
Q=0(since cos(0)−1=0)
2. When θ=90∘:
Q=−n⋅B⋅AR⋅(−1)⋅t=n⋅B⋅A⋅tR
3. When θ=180∘:
Q=−n⋅B⋅AR⋅(1−(−1))⋅t=0(since cos(180)−1=−2)
4. When θ=360∘:
Q=0(since it returns to the initial position)
Conclusion
The correct alternatives are:
- When θ=90∘, Q is maximum.
- When θ=0∘ or 180∘ or 360∘, Q=0.
Initially, the plane of the coil is parallel to the magnetic field B. The area vector →A of the coil is also parallel to B. Therefore, the initial angle θi=0∘.
The magnetic flux Φ through the coil is given by:
Φ=B⋅A⋅cos(θ)
Where:
- B is the magnetic field strength,
- A is the area of the coil,
- θ is the angle between the area vector and the magnetic field.
Φi=B⋅A⋅cos(0)=B⋅A
After rotating the coil by an angle θ, the new angle θf becomes θ. Thus, the final magnetic flux is:
Φf=B⋅A⋅cos(θ)
The change in magnetic flux ΔΦ is given by:
ΔΦ=Φf−Φi=B⋅A⋅cos(θ)−B⋅A=B⋅A(cos(θ)−1)
According to Faraday's law of electromagnetic induction, the induced EMF E in the coil is given by:
E=−dΦdt
For a finite change, we can express it as:
E=−nΔΦΔt
Where n is the number of turns in the coil.
Using Ohm's law, the current I flowing through the coil can be expressed as:
I=ER
Where R is the resistance of the coil.
The charge Q that flows through the coil can be calculated using the relationship:
Q=I⋅t
Substituting for I:
Q=ER⋅t
Substituting for E:
Q=−nR⋅ΔΦ
Substituting for ΔΦ:
Q=−nR⋅B⋅A(cos(θ)−1)⋅t
1. When θ=0∘:
Q=0(since cos(0)−1=0)
Q=−n⋅B⋅AR⋅(−1)⋅t=n⋅B⋅A⋅tR
Q=−n⋅B⋅AR⋅(1−(−1))⋅t=0(since cos(180)−1=−2)
Q=0(since it returns to the initial position)
The correct alternatives are:
- When θ=90∘, Q is maximum.
- When θ=0∘ or 180∘ or 360∘, Q=0.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Asserton - Reasoning
8 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Linked Comprehension
36 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercises Single Correct
79 Videos
- ELECTRICAL MEASURING INSTRUMENTSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRICAL MEASURING INSTRUMENTSEXERCISE - M.C.Q
2 Videos
- ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRON,PHONTS,PHOTOELECTRIC EFFECT & X-RAYSEXERCISE - dpp 3.3
15 Videos
Similar Questions
A flat coil, C, of n turns, area A and resistance R, is placed in a uniform magnetic field of magnitude B. The plane of the coil is initially perpendicular to B. The coil,is rotated by an angle θ about a diameter and charge of amount Q flows through it. Choose the correct alternatives.
View SolutionA flat circular coil of n turns, area A and resitance R is placed in a uniform magnetic field B. The pane of coil is initially perpedicular of B. when the coil is rotated through an angle of 180∘ about one of its diameter, a charge Q1 flows through the coil When the same coil after charge Q2 flows through it. then Q2/Q1 is
View SolutionInitially plane of coil is parallel to the uniform magnetic field B. In time Δt it makes to perpendicular to the magnetic field, then charge flows in Δt depends on this time as -
View SolutionShow that a ray of light reflected from a plane mirror rotates througha an angle 2θ when the
mirror is rotated through an angle θ about its axis perpendicular to both the incident ray and
the normal to the surface.
View SolutionA circular coil of radius 10 cm is placed in uniform magnetic field of 3.0×10−5 T with its plane perpendicular to the field initially. It is rotated at constant angular speed about an axis along the diameter of coil and perpendicular to magnetic field so that it undergoes half of rotation in 0.2s. The maximum value of EMF induced (inμV) in the coil will be close to the integer._________.
View SolutionA flip coil consits of N turns of circular coils which lie in a uniform magnetic field. Plane of the coils is perpendicular to the magnetic field as shown in figure. The coil is connected to a current integrator which measures the total charge passing through it. The coil is turned through 180∘ about the diameter. The charge passing through the coil is
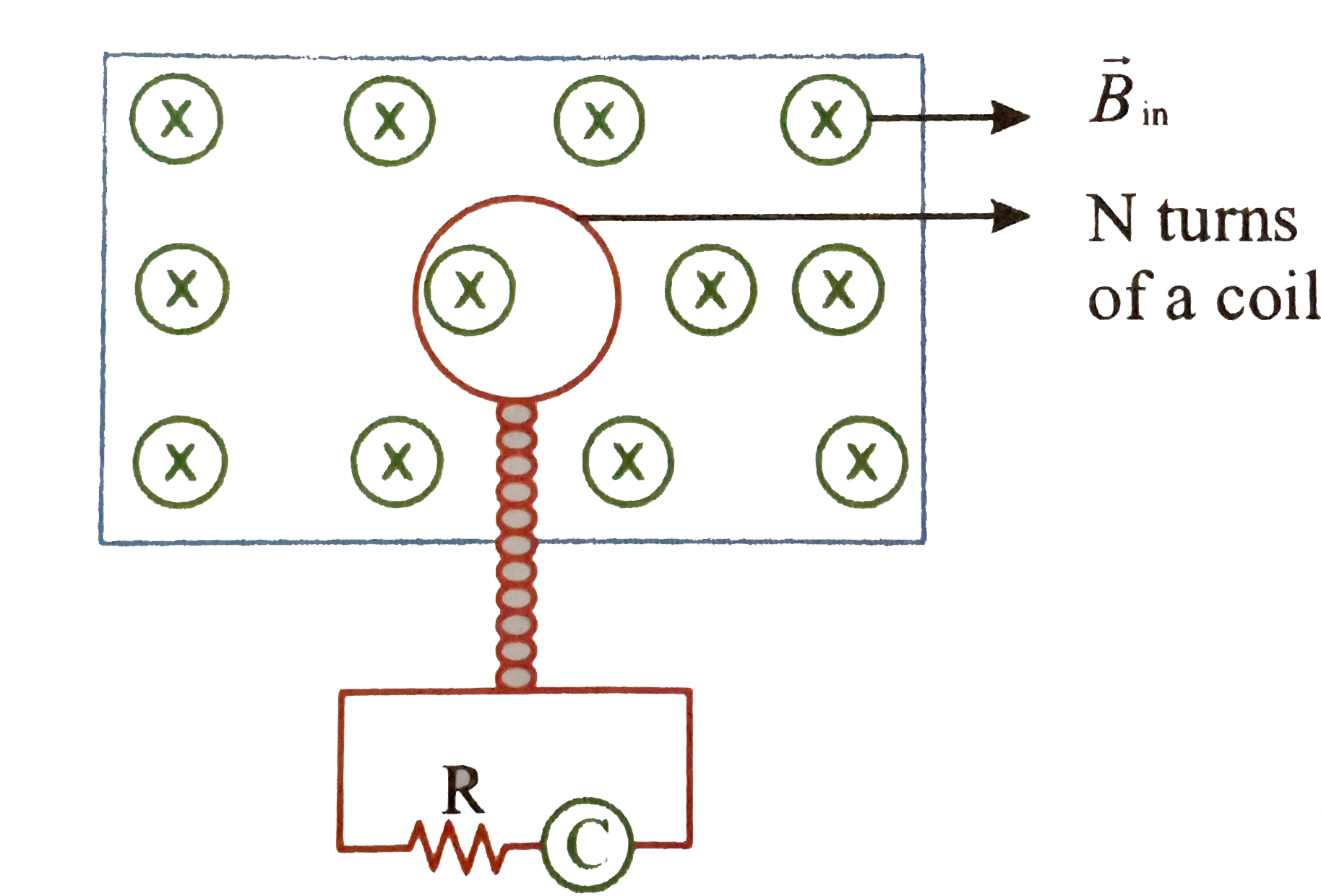
View SolutionIn Fig. a coil of single turn is wound on a sphere of radius r and mass m. The plane of the coil is parallel to the inclined plane and lies in the equatorial plane of the sphere. If the sphere is in rotational equilibrium, the value of B is [Current in the coil is i]
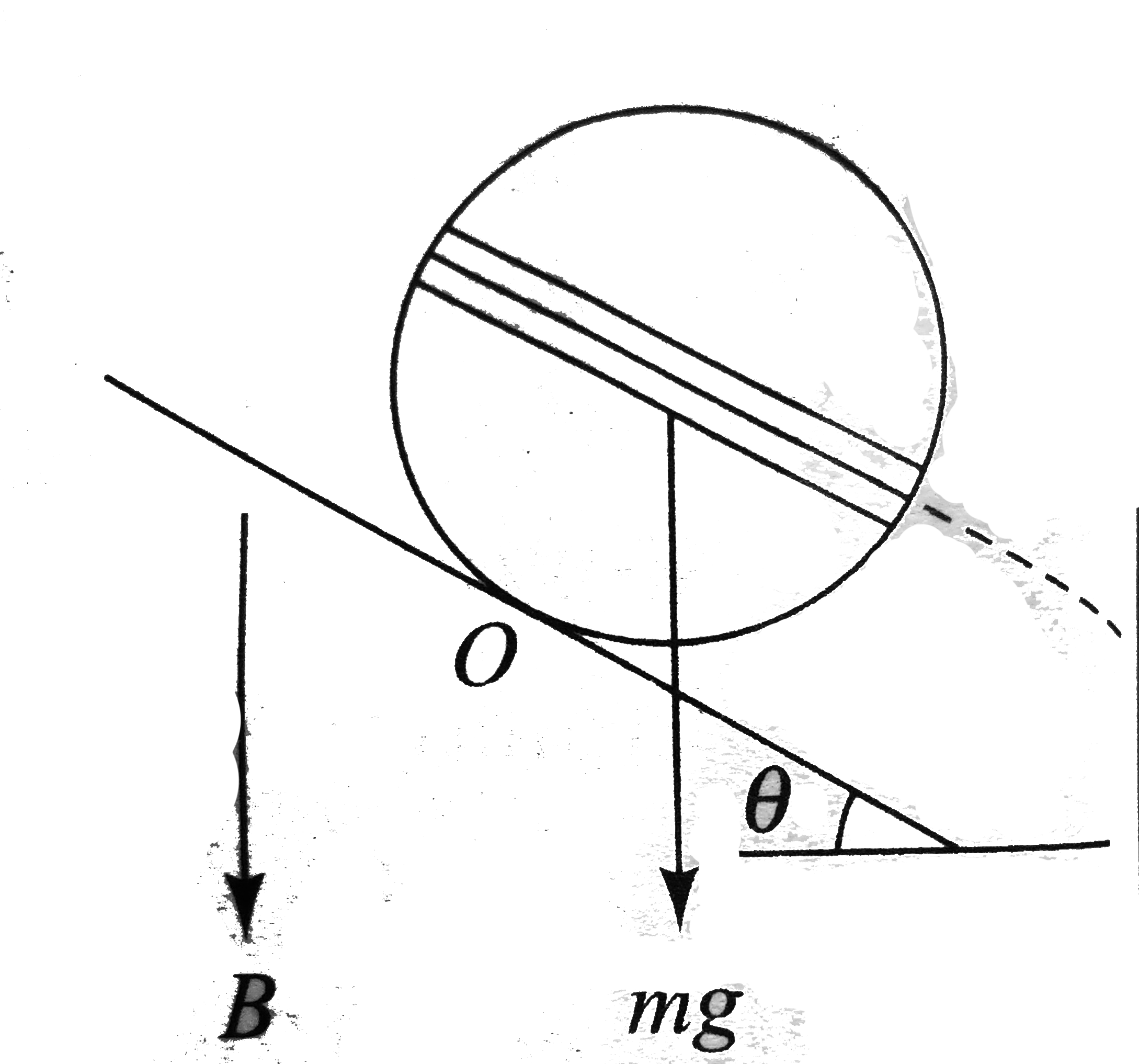
View SolutionA circular coil of n turns and area of crosssection A , carrying a current i, rests with its plane normal to an external magnetic field B. The coil is free to turn about an axis in its plane perpendicular to the field direction. If the moment of inertia of the coil about its axis of rotation is I, its frequency of oscillation about its stable equilibrium is given by
View Solution
in given circuit initially both capacitors were uncharged. Amount of total charge that will flow through point B when the switch s is closed is:
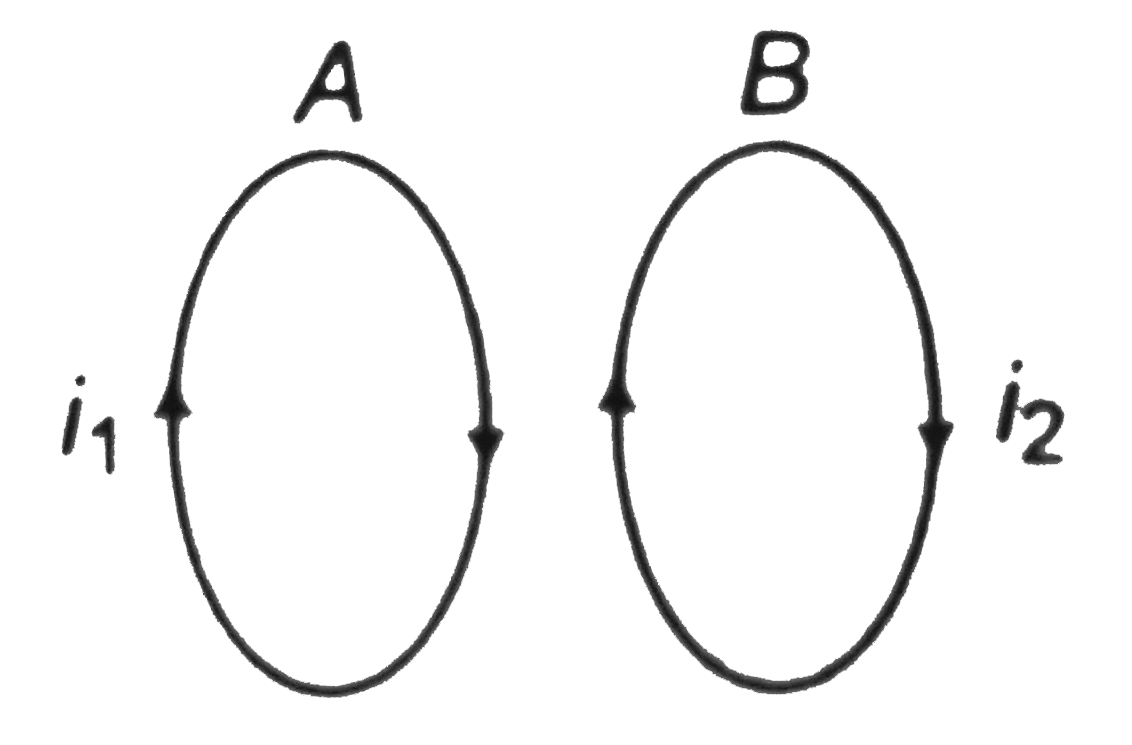
View SolutionTwo circular coils are placed adjacent to each other. Their planes are parallel and currents through them i1 and i2 are in same direction. Choose the correct options.
View Solution
