In the arrangement shown above, all surfaces are frictionless. The rod R is constrained to move vertically. The vertically acceleration of R is $a_{1}$ and the horizontal accelration of the wedge W is $a_{2}$ . The ratio $a_{1} / a_{2}$ is equal to

A

$tan α$

B

$cot α$

C

$sin α$

D

$cos α$

Text Solution

Verified by Experts

The correct Answer is:A

|

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Topper's Solved these Questions

BOOK - D MUKHERJEECHAPTER - PRACTICE WORKSHEET 3EXERCISE - Assertion- Reason Type
3videos
PRACTICE WORKSHEET 3
BOOK - D MUKHERJEECHAPTER - PRACTICE WORKSHEET 3EXERCISE - Linked- Comprehension Type
3videos
PRACTICE WORKSHEET 3
BOOK - D MUKHERJEECHAPTER - PRACTICE WORKSHEET 2EXERCISE - Linked- Comprehension Type
4videos
PRACTICE WORKSHEET 2
BOOK - D MUKHERJEECHAPTER - PROPERTIES OF MATTER,FLUIDSEXERCISE - Type 2
35videos
PROPERTIES OF MATTER,FLUIDS

Similar Questions

Knowledge Check

Question 1 - Select One
Let $a_{1}, a_{2}, a_{3}$ be three positive numbers which are in geometric progression with common ratio r. The inequality $a_{3} > a_{2} + 2 a_{1}$ holds true if r is equal to
A2
B1.5
C0.5
D2.5
Question 2 - Select One
Let $a_{1}, a_{2}, a_{3}$ , be three positive numbers which are $G . P .$ with common ratio r. The inequality $a_{3} > a_{2} + 2 a_{1}$ do not holds if r is equal to
A2
B1.5
C0.5
D2.5
Question 3 - Select One
A pulley-block arrangement is shown in the adjacent figure, if acceleration of $m_{1}, m_{2}$ and $m_{3}$ are $a_{1}, a_{2}$ and $a_{3}$ respectively, then relation between $a_{1}, a_{2}$ and $a_{3}$ is ( All string and pulleys are ideal . )

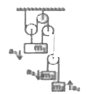A $a_{2} - a_{3} + 10 a_{1} = 0$
B $a_{3} - a_{2} + 10 a_{1} = 0$
C $a_{2} - 2 a_{3} + 10 a_{1} = 0$
D $2 a_{2} + a_{3} + 5 a_{1} = 0$

D MUKHERJEE-PRACTICE WORKSHEET 3-Matrix-Matching Type

Home
Ask Doubt
Profile