In the circuit below, the AC source the voltage V=20cos(ωt) volts with ω=2000rad/sec. The amplitude of the current will be nearest to

2:0
3.3 A
2√5 A
√5 A
The correct Answer is:A
Total resistance of the circiut,
R = 6 + 4 = 10Ω
Capacitive reactance,
XC=1ωC=12000×50×10−6 = 10Ω
Inductive reactance,
XL = ωL = 2000×5×10−3 = 10Ω
∴ Z = √R2+(XL−XC)2 = 10Ω
Amplitude of current , I0 = V0Z=2010=2A.
Similar Questions
In the circuit shown the source voltage is given asv=V0 sin ωt. Find the current through the source as a function of time.
 View Solution
View SolutionIn the given circuit the AC source has ω=100rads−1. Considering the inductor and capacitor to be ideal, what will be the current I flowing through the circuit ?
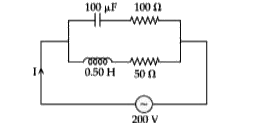 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
In the circuit below, the AC source the voltage V=20cos(ωt) volts with ω=2000rad/sec. The amplitude of the current will be nearest to
 A2AB3.3AC2/√5AD√5A
A2AB3.3AC2/√5AD√5A - Question 2 - Select One
In the circuit shown in figure, the AC source gives a voltage V = 20 cos(2000 t ) . Neglecting source resistance, the voltmeter and ammeter readings will be (approximately)
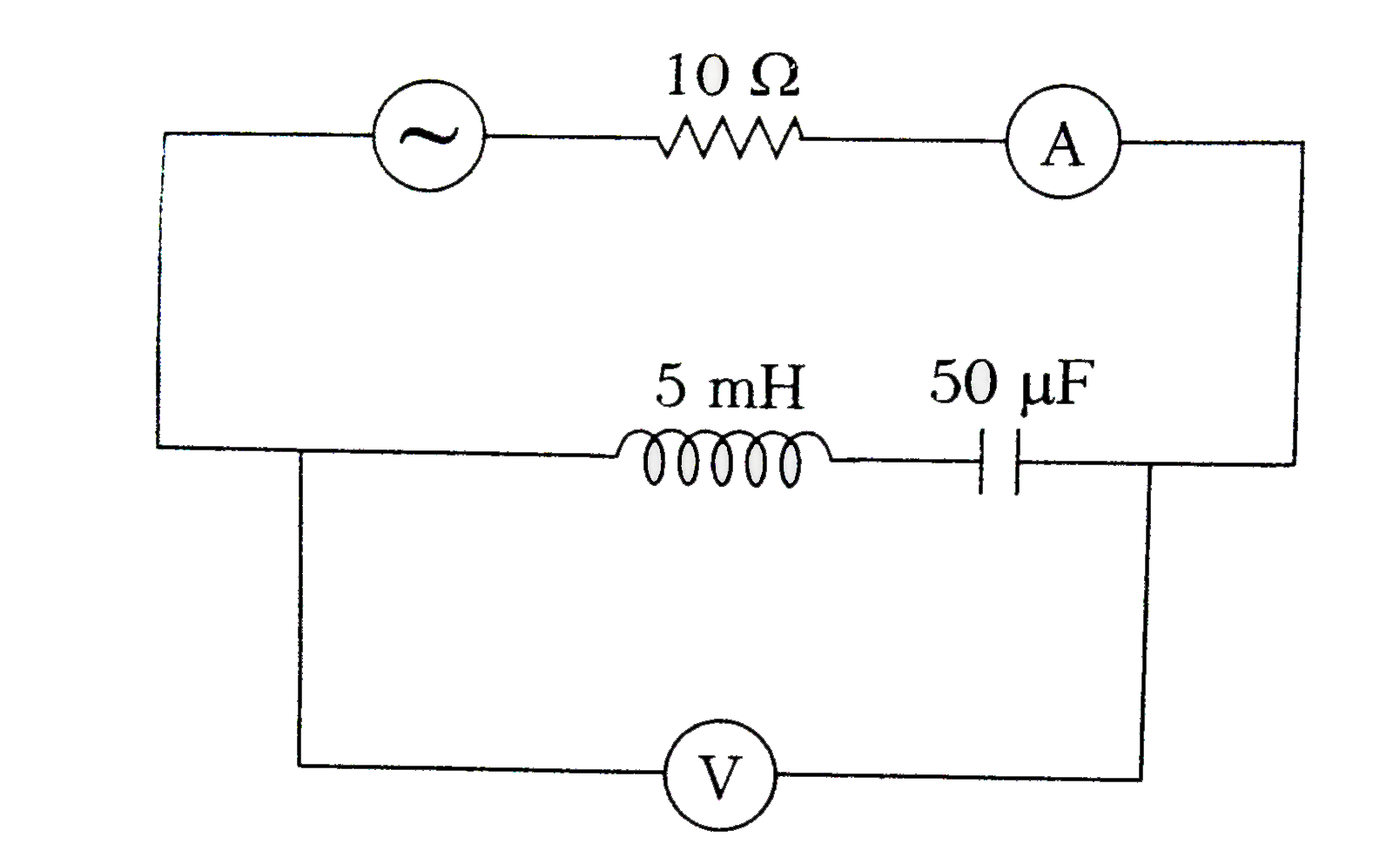 A4 V, 2.0 AB0 V, 2 AC0 V, 1.4 AD8 V, 2.0 A
A4 V, 2.0 AB0 V, 2 AC0 V, 1.4 AD8 V, 2.0 A - Question 3 - Select One
In the circuit shown in figure the AC source gives a voltage V=20cos(2000t). Neglecting source resistance, the voltmeter and and ammeter readings will be
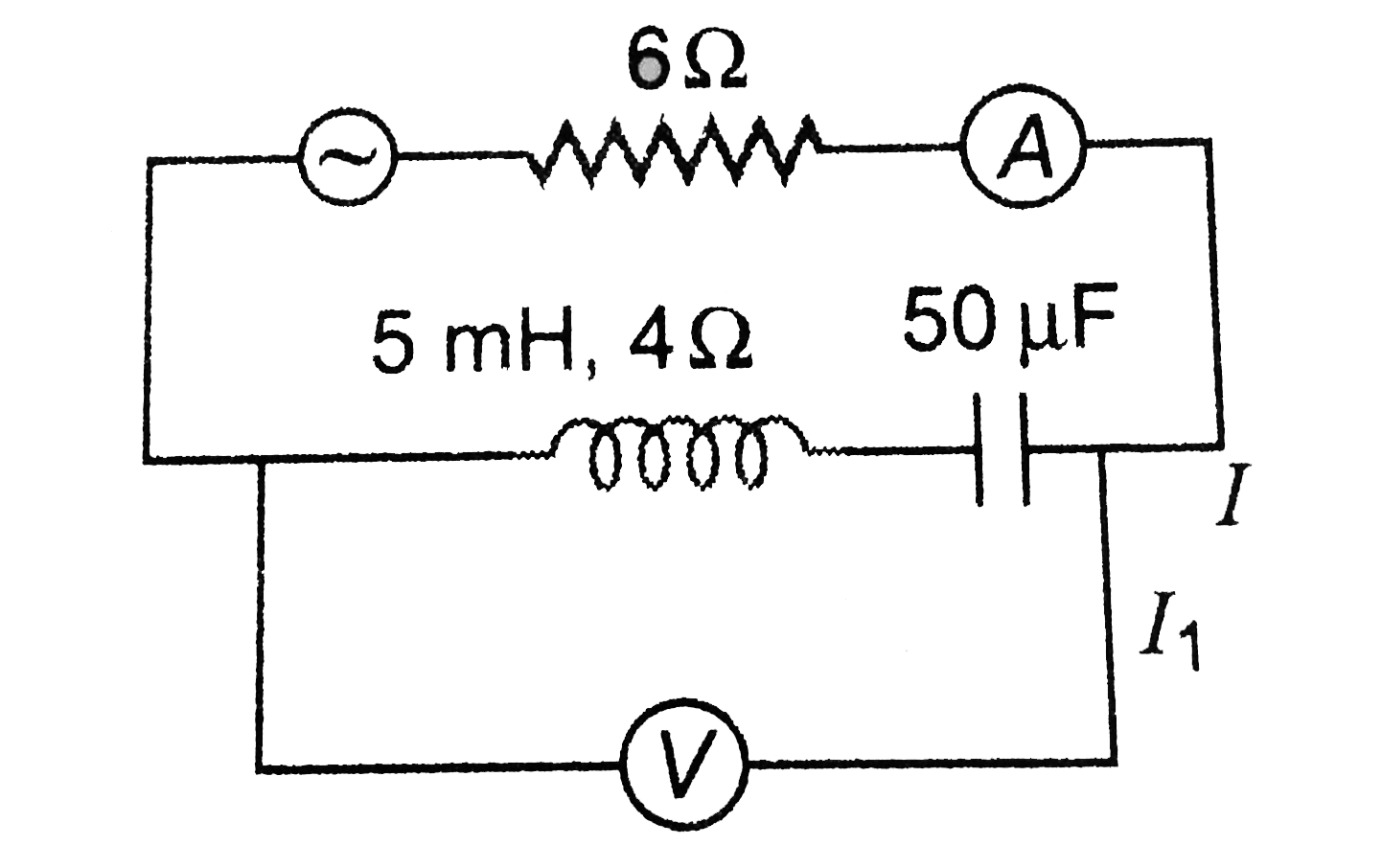 .A0V,2.0AB0V,1.4AC5.6V,1.4AD8V,2.0A
.A0V,2.0AB0V,1.4AC5.6V,1.4AD8V,2.0A
A capacitor of capacitive reactance 5ω is connected with A.C. source having voltage V=3sin(ωt+π/6). Find rms and Peak voltage rms and peak current and instantaneous current
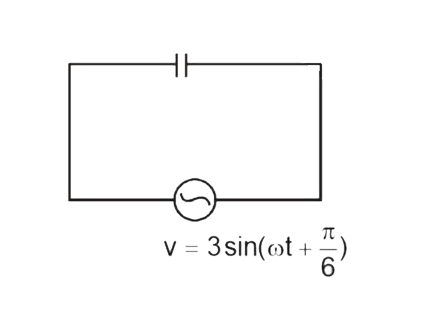 View Solution
View SolutionIn the given circuit, the AC source has ω = 100 rad/s. Considering the inductor and capacitor to be ideal, the correct choice(s) is (are)
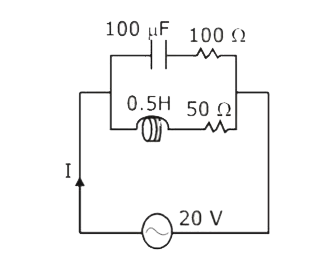 View Solution
View SolutionIn the given circuit, the AC source has ω=50rad/s. Considering the inductor and capacitor to be ideal, the correct choice (s) is (are):
 View Solution
View SolutionIn a LR circuit of 3 mH dinductance and 4Ω resistance, emf E=4cos1000t volt is applied. The amplitude of current is
View SolutionIn the circuit of fig, the source freqency is ω=2000rads−1. The current in the will be
 View Solution
View Solution

