In the determination if Young's modulus ((Y=4MLgπld2 by using searle's method, a wire of length L=2m and diameter d=0.5mm is used. For a load M=2.5kg, an extension l=0.25mm in the length of the wire is observed. Quantites Dandl are measured using a screw gauge and a micrometer, respectively. they have the same pitch of 0.5mm. the number of divisions on their circular scale is 100. the contrubution to the maximum probable error of the Y measurement
due to the error in the measurements of dandl are the same.
due to the error in the measurements of d is twice that due to the error in the measurement of l.
due to the error in the measurements of l is twice that due to the error in the measurement of d.
due to the error in the measurements of d is four times that due to the error in the measurement of l.
The correct Answer is:A
To determine the contribution to the maximum probable error of Young's modulus Y in the given scenario, we will follow these steps:
Step 1: Understand the formula for Young's modulus
The formula for Young's modulus is given by:
Y=4MLgπd2
where:
- M = mass (in kg)
- L = original length of the wire (in m)
- g = acceleration due to gravity (approximately 9.81m/s2)
- d = diameter of the wire (in m)
Step 2: Identify the parameters and their values
From the problem:
- L=2m
- d=0.5mm=0.5×10−3m=5×10−4m
- M=2.5kg
- Extension l=0.25mm=0.25×10−3m=2.5×10−4m
Step 3: Calculate the possible errors in measurements
The error in measurement for both L and d can be calculated using the pitch and the number of divisions on the circular scale.
Given:
- Pitch = 0.5mm=0.5×10−3m
- Number of divisions = 100
The least count (LC) for both the screw gauge and micrometer is:
LC=PitchNumber of divisions=0.5×10−3100=5×10−6m
Thus, the possible errors in measurements ΔL and Δd are:
ΔL=Δd=5×10−6m
Step 4: Calculate the percentage error in L and d
The percentage error in L is calculated as:
Percentage error in L=(ΔLL)×100=(5×10−62)×100=0.00025×100=0.025%
The percentage error in d is calculated as:
Percentage error in d=(Δdd)×100=(5×10−65×10−4)×100=0.01%
Step 5: Calculate the contribution to the error in Y
The contributions to the error in Y are based on the powers of L and d in the formula for Young's modulus:
- The power of L in the formula is 1.
- The power of d in the formula is 2.
Thus, the contributions to the percentage error in Y are:
Contribution from L=1×Percentage error in L=1×0.025%=0.025%
Contribution from d=2×Percentage error in d=2×0.01%=0.02%
Step 6: Total contribution to the maximum probable error in Y
Now, we sum the contributions:
Total contribution to error in Y=0.025%+0.02%=0.045%
Final Answer
The contribution to the maximum probable error of the Young's modulus Y measurement is approximately 0.045%.
The formula for Young's modulus is given by:
Y=4MLgπd2
where:
- M = mass (in kg)
- L = original length of the wire (in m)
- g = acceleration due to gravity (approximately 9.81m/s2)
- d = diameter of the wire (in m)
From the problem:
- L=2m
- d=0.5mm=0.5×10−3m=5×10−4m
- M=2.5kg
- Extension l=0.25mm=0.25×10−3m=2.5×10−4m
The error in measurement for both L and d can be calculated using the pitch and the number of divisions on the circular scale.
- Pitch = 0.5mm=0.5×10−3m
- Number of divisions = 100
LC=PitchNumber of divisions=0.5×10−3100=5×10−6m
ΔL=Δd=5×10−6m
The percentage error in L is calculated as:
Percentage error in L=(ΔLL)×100=(5×10−62)×100=0.00025×100=0.025%
Percentage error in d=(Δdd)×100=(5×10−65×10−4)×100=0.01%
The contributions to the error in Y are based on the powers of L and d in the formula for Young's modulus:
- The power of L in the formula is 1.
- The power of d in the formula is 2.
Contribution from L=1×Percentage error in L=1×0.025%=0.025%
Contribution from d=2×Percentage error in d=2×0.01%=0.02%
Now, we sum the contributions:
Total contribution to error in Y=0.025%+0.02%=0.045%
The contribution to the maximum probable error of the Young's modulus Y measurement is approximately 0.045%.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Multiple correct Answer Type8videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Integer2videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - DIMENSIONS & MEASUREMENTEXERCISE - Fill In The Blanks4videos
DIMENSIONS & MEASUREMENT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENTRE OF MASSEXERCISE - INTEGER_TYPE1videos
CENTRE OF MASS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - FLUID MECHANICSEXERCISE - INTEGER_TYPE1videos
FLUID MECHANICS
Similar Questions
The figure shows the variation of energy with the orbit radius of a body in circular planetary motion.
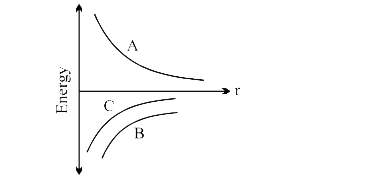
Find the correct statement about the curves A, B and CView SolutionA wire 3m long and diameter 0.3 mm is stretched by a load of 2kg. If the elongation is 2mm, find the Young.s modulus of the material of the wire and the potential energy stored in the wire.
View Solutionthe least count of the main scale of a screw gauge is 1 mm. the minimum number of divisions on its circular scale required to measure 5μm diameter of a wire is :
View SolutionWhen a wire of length 5m and diameter 1mm was stretched by a load of 5kg the elongation produced in the wire was 1mm. Find the energy stored in per unit volume of the wire?
View SolutionA screw gauge has least count of 0.01 mm and there are 50 divisions in its circular scale:
The pitch of the screw gauge is:View SolutionIn an internal micrometer, main scale division is of 0.5 mm and there are 50 divisions in circular scale. The least count of the instrument is-
View SolutionA steel wire of length 4 m and diameter 5 mm is strethed by 5 kg-wt. Find the increase in its length, if the Young's modulus of steel is 2×1012 dyne cm2
View SolutionA steel wire of length 4 m and diameter 5 mm is stretched by 5kg-wt. Find the increase in its length if the Young's modulus of steel wire is 2.4×1012dynecm−2
View SolutionA wire of length 15m and diameter 4 mm elongates 0.3mm when stretched by weigth of 2.20kg. Calulate the Young's modulus of the material of the wire.
View SolutionIf the length of wire is (100.0 cm) and radius of wire as measured from screw gauge is (1.00mm) then the specific resistance of wire material is .
View Solution

