In the diagrams, all the light bulbs are identical, and all cells are ideal and identical. In which circuit (a,b, c,d) will the bulbs be dimmest ?

The correct Answer is:C
To determine which circuit (A, B, C, or D) has the dimmest bulbs, we will analyze the power delivered to the bulbs in each circuit. The power (P) of a bulb can be expressed as:
P=V2R
where V is the voltage across the bulb and R is the resistance of the bulb. Since all bulbs are identical, we can focus on the voltage across each bulb in each circuit.
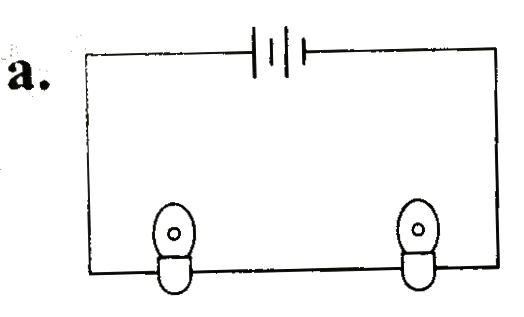
Step 1: Analyze Circuit A
- In Circuit A, there are 2 cells connected in series providing a total voltage of 2ϵ.
- There are 2 bulbs connected in series, so the voltage across each bulb is 2ϵ2=ϵ.
- The power for each bulb is:
PA=ϵ2R
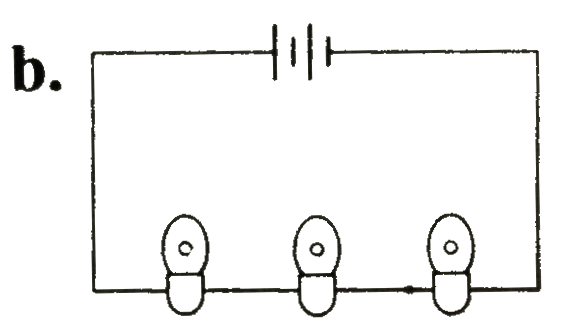
Step 2: Analyze Circuit B
- In Circuit B, there are 3 cells connected in series providing a total voltage of 2ϵ.
- There are 3 bulbs connected in series, so the voltage across each bulb is 2ϵ3.
- The power for each bulb is:
PB=(2ϵ3)2R=4ϵ29R
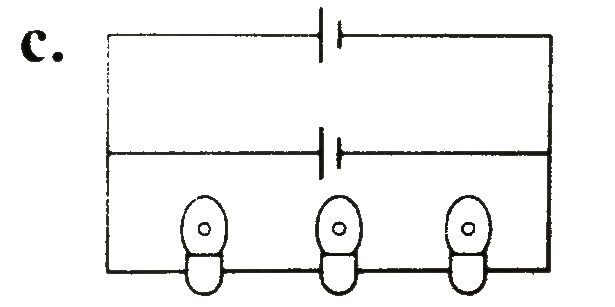
Step 3: Analyze Circuit C
- In Circuit C, there are 3 cells connected in parallel providing a total voltage of ϵ.
- The voltage across each bulb is ϵ3 (since they are in parallel).
- The power for each bulb is:
PC=(ϵ3)2R=ϵ29R
Step 4: Analyze Circuit D
- In Circuit D, there are 2 cells connected in parallel providing a total voltage of 2ϵ.
- The voltage across each bulb is 2ϵ.
- The power for each bulb is:
PD=(2ϵ)2R=4ϵ2R
Step 5: Compare the Powers
Now we compare the powers calculated for each circuit:
- PA=ϵ2R
- PB=4ϵ29R
- PC=ϵ29R
- PD=4ϵ2R
From the calculations:
- PA>PB>PC<PD
Conclusion
The circuit with the dimmest bulbs is Circuit C, as it has the least power delivered to each bulb.
Final Answer
The bulbs will be dimmest in Circuit C.
---
- In Circuit A, there are 2 cells connected in series providing a total voltage of 2ϵ.
- There are 2 bulbs connected in series, so the voltage across each bulb is 2ϵ2=ϵ.
- The power for each bulb is:
PA=ϵ2R
- In Circuit B, there are 3 cells connected in series providing a total voltage of 2ϵ.
- There are 3 bulbs connected in series, so the voltage across each bulb is 2ϵ3.
- The power for each bulb is:
PB=(2ϵ3)2R=4ϵ29R
- In Circuit C, there are 3 cells connected in parallel providing a total voltage of ϵ.
- The voltage across each bulb is ϵ3 (since they are in parallel).
- The power for each bulb is:
PC=(ϵ3)2R=ϵ29R
- In Circuit D, there are 2 cells connected in parallel providing a total voltage of 2ϵ.
- The voltage across each bulb is 2ϵ.
- The power for each bulb is:
PD=(2ϵ)2R=4ϵ2R
Now we compare the powers calculated for each circuit:
- PA=ϵ2R
- PB=4ϵ29R
- PC=ϵ29R
- PD=4ϵ2R
- PA>PB>PC<PD
The circuit with the dimmest bulbs is Circuit C, as it has the least power delivered to each bulb.
The bulbs will be dimmest in Circuit C.
Similar Questions
In the diagrams, all light bulbs are identical and all emf sources are ideal and identical. In which circuit (given in option) will each bulb glow with the same brightness as in the circuit shown?
 View Solution
View SolutionIn the circuit diagram, all the bulbs are identical. Which bulb will be the brightest?
 View Solution
View SolutionAll eukaryotic cells are not identical
View SolutionAll atoms of an element are identical.
View SolutionIf all the resistors are identical , select the correct alternative (s).
 View Solution
View SolutionThe light bulb A & B in the following circuits are identical. When the switch is closed
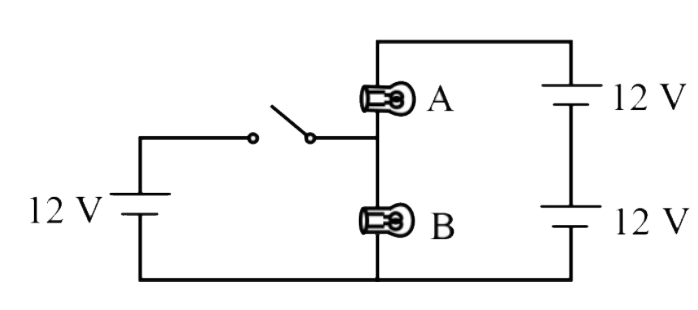 View Solution
View SolutionIn these circuits all the batteries are indentical and have negllgible internal resistance, and all the light bulbs are indentical. Rank all 5 light bulbs (A, B, C, D, E) in order of brightness from brightness to dimmet.
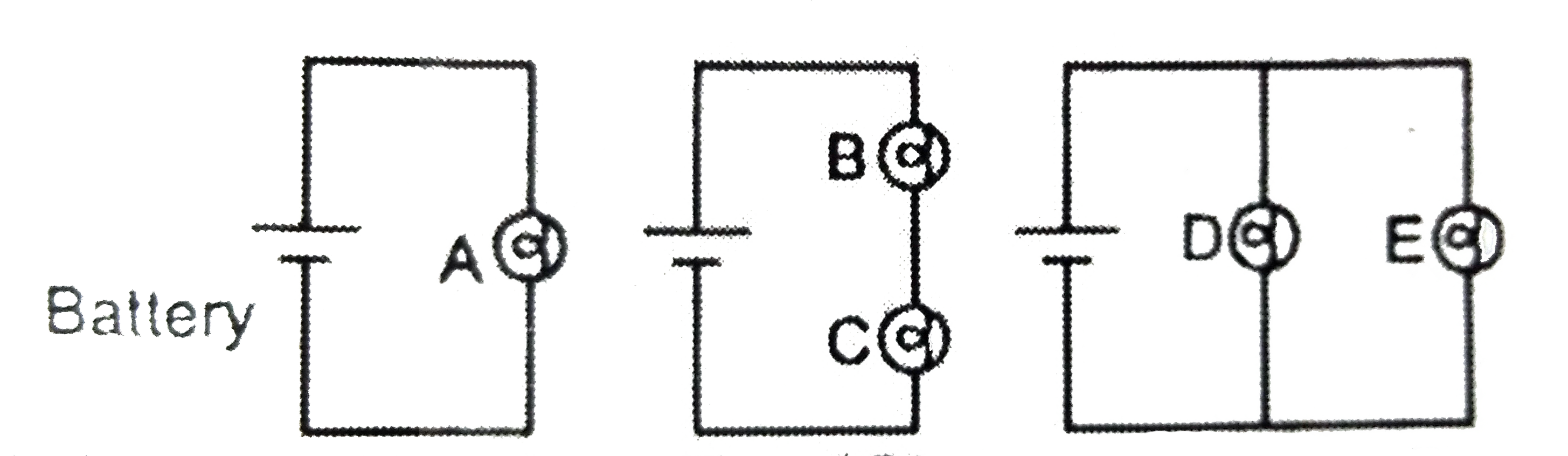 View Solution
View SolutionAssuming all bulbs are identical, rank the brightness of the bulbs, from brightest to dimmest.
 View Solution
View SolutionAll the bulbs below are identical. Which bulb(s) shine(s) most brightly?
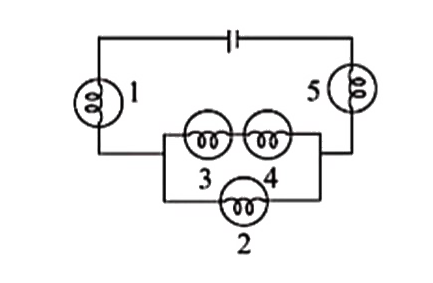 View Solution
View Solutionn identical bulbs are connected in series and illuminated by a power supply . One of the bulbs gets fused. The fused bulb is removed , and the remaining bulbs are again illuminated by the same power supply. Find the fractional change in the illuminated of (a) all the bulbs and (b) one bulb.
View Solution

