In the Fig, shown below with what angular speed ' ' must 'm' with a radius 'r' rotate on a frictionless table so that' M' does not move ? (b) If m = 1.0 kg, M = 10.0 kg and r = 0.5 m, find
To solve the problem, we need to analyze the forces acting on the mass 'm' that is rotating on a frictionless table while being connected to a mass 'M' hanging vertically.
1. Identify the Forces:
- The mass 'M' hanging vertically exerts a gravitational force downwards, which is equal to M⋅g, where g is the acceleration due to gravity (approximately 9.8m/s2).
- The tension T in the string acts upwards on mass 'M' and provides the necessary centripetal force for mass 'm' to rotate.
2. Set Up the Equations:
- For the mass 'M', the forces can be balanced as:
T=M⋅g
- For the mass 'm' rotating in a circle of radius r, the centripetal force required is provided by the tension in the string:
T=m⋅r⋅ω2
3. Equate the Two Expressions for Tension:
- Since both expressions represent the tension T, we can set them equal to each other:
M⋅g=m⋅r⋅ω2
4. Solve for Angular Speed ω:
- Rearranging the equation to solve for ω2:
ω2=M⋅gm⋅r
- Taking the square root to find ω:
ω=√M⋅gm⋅r
5. Substituting the Given Values:
- Given m=1.0kg, M=10.0kg, r=0.5m, and g=9.8m/s2:
ω=√10.0⋅9.81.0⋅0.5
6. Calculating the Value:
- Calculate the numerator:
10.0⋅9.8=98.0
- Calculate the denominator:
1.0⋅0.5=0.5
- Now calculate ω:
ω=√98.00.5=√196=14rad/s
Final Answer:
The angular speed ω must be 14rad/s.
- The mass 'M' hanging vertically exerts a gravitational force downwards, which is equal to M⋅g, where g is the acceleration due to gravity (approximately 9.8m/s2).
- The tension T in the string acts upwards on mass 'M' and provides the necessary centripetal force for mass 'm' to rotate.
- For the mass 'M', the forces can be balanced as:
T=M⋅g
- For the mass 'm' rotating in a circle of radius r, the centripetal force required is provided by the tension in the string:
T=m⋅r⋅ω2
- Since both expressions represent the tension T, we can set them equal to each other:
M⋅g=m⋅r⋅ω2
- Rearranging the equation to solve for ω2:
ω2=M⋅gm⋅r
- Taking the square root to find ω:
ω=√M⋅gm⋅r
- Given m=1.0kg, M=10.0kg, r=0.5m, and g=9.8m/s2:
ω=√10.0⋅9.81.0⋅0.5
- Calculate the numerator:
10.0⋅9.8=98.0
- Calculate the denominator:
1.0⋅0.5=0.5
- Now calculate ω:
ω=√98.00.5=√196=14rad/s
The angular speed ω must be 14rad/s.
Similar Questions
Three blocks of masses m1,m2andm3 are connected by mass less string as shown kept on a frictionless table.

They are pulled with a force T3=40N. If m1=10kg,m2=6kgandm3=4kg, the tension T2 will be
View SolutionA sphere of mass 10 kg and radius 0.5 m rotates about a tangent. The moment of inertia of the sphere is
View SolutionA disc of mass m and radius R rotating with angular speed ω0 is placed on a rough surface (co-officient of friction =μ). Then

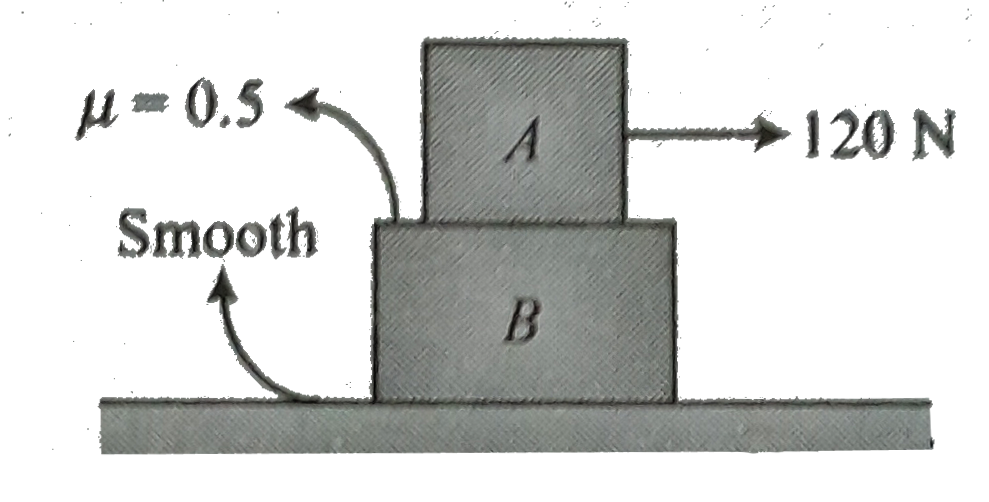
View SolutionFind the acceleration of the two blocks . The system is initialy at rest and the friction are as shown in fig .Given mA=mB=10kg
View SolutionA uniform disc of mass m, radius R is placed on a smooth horizontal surface. If we apply a horizontal force F at P as shown in the figure. If F=4N,m=.1kg,R=1m and r=12m then, find the:
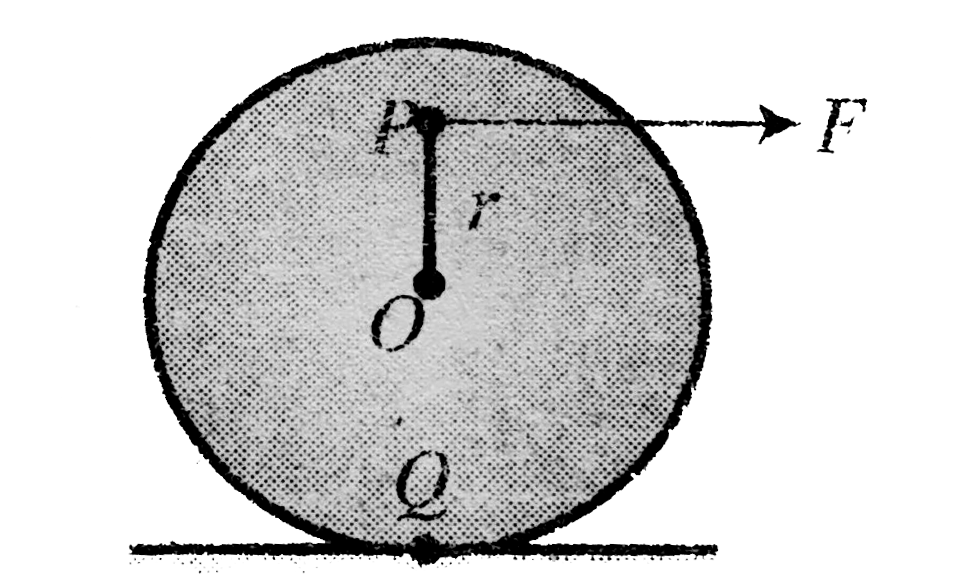
angular acceleration of the disc. (rads−1)
View SolutionFind the maximum possible percentage error in the measurement of force on an object (of mass m) travelling at velocity v in a circle of radius r if m =(4.0±0.1)kg, v= (10±0.1) m/s and r=(8.0±0.2) m
View SolutionThere are two blocks of masses m1 and m2,m1 is placed on m2 on a table which is rotating with an angular velocity ω about the vertical axis . The coefficent of friction between the block is μ1 and between m2 and table is μ2(μ1<μ2) if block are placed at distance R from the axis of ratation , for relative sliding between the surface in contact , find the
a. friction force at the contacting surface
b. maximum angular speed ω

View SolutionThree blocks of masses m1,m2and m3 are connected by massless strings as shown on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kg and m3=4kg the tension T2 will be

View SolutionTwo particles of mass M=3kg each are kept on a horizontal circular platform on two mutually perpendicular radii at equal distance R=1m from the centre of the table. The particles are connected with a string,which is just taught when the platform is not rotating.Coefficient of friction between the platform and block is μ=0.4.Then the maximum angular speed (ω in radsec) of platform about its centre so that the blocks remain stationary relative to platform is (take g=10.ms2 )
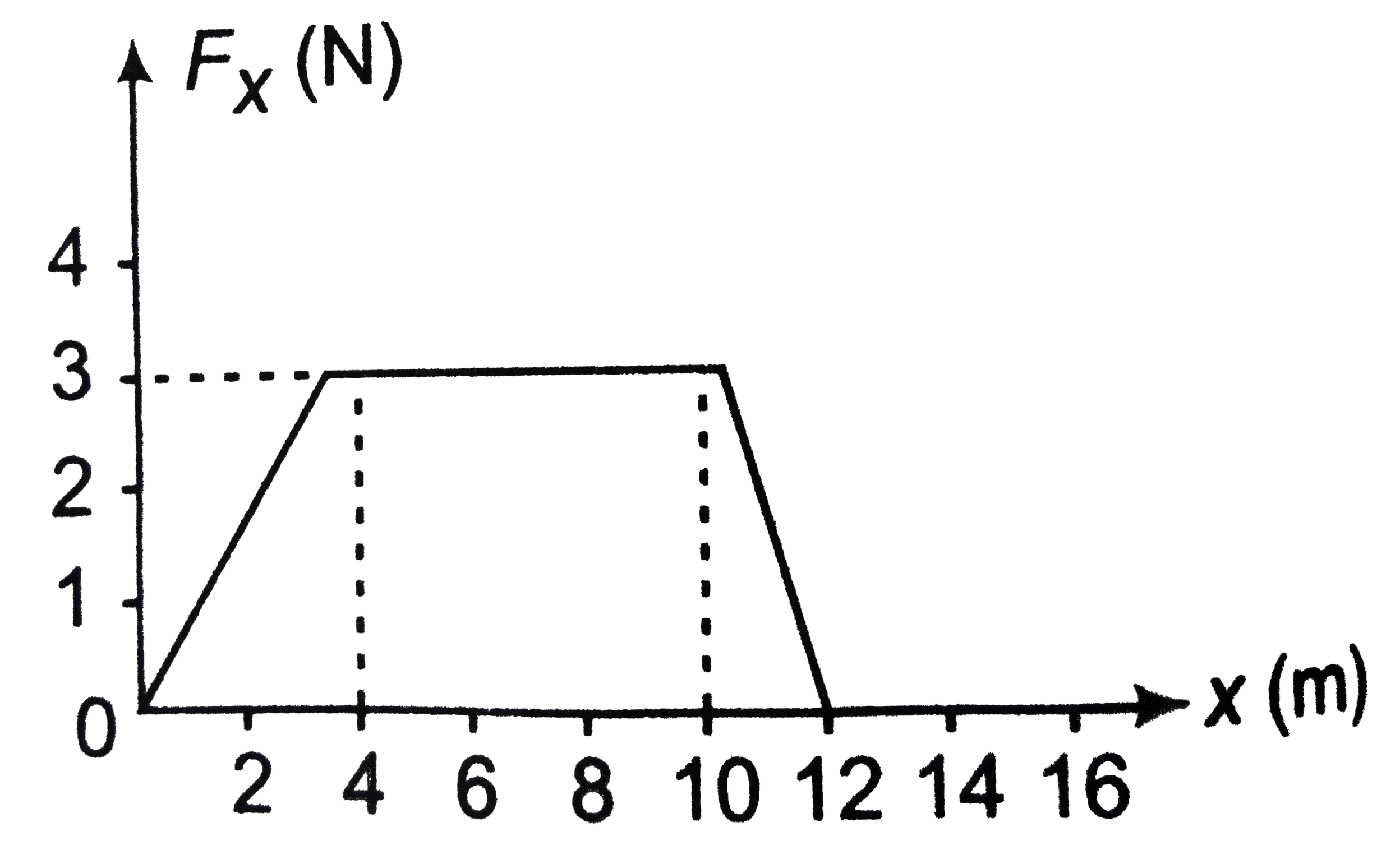
View SolutionA particle is subjected to a force Fx that varies withes position as shown in figure. Find the work done by the force on the body as it moves
(a) from x=10.0m to x=5.0m,
(b) from x=5.0m to x=10.0m,
(c ) from x=10.0m to x=15.0m,
(d) what is the total work done by the force over the distance x=0 to x=15.0?
 .
.
View Solution
