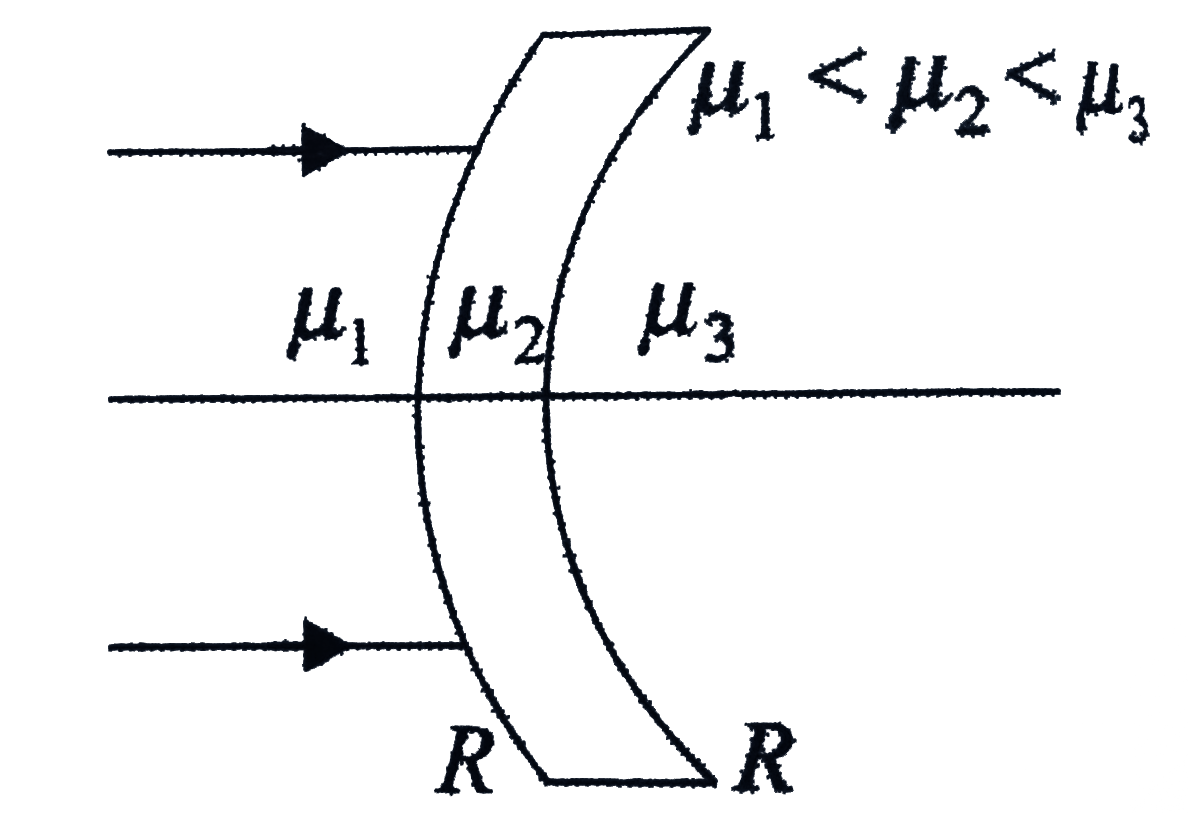
In the figure, light is incident on a thin lens as shown. The radius of curvature for both the surfaces is R. Determine the focal length of this system. 
For refraction at first surface,
μ2v1−μ1−∞=μ2−μ1+R………(i)
For refraction at second surface,
μ3v2−μ2v1=μ3−μ2+R …………(ii)
Adding Eqs. (i) and (ii), we get μ3v2−μ2−μ1Rorv2=μ3Rμ3−μ1

Therefore, focal length of the given lens system is
f=μ3Rμ3−μ1
Topper's Solved these Questions
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Solved Example
15 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Exercise 31.1
3 Videos
- REFRACTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFRACTION OF LIGHTEXERCISE - Example Type 10
1 Video
- REFLECTION OF LIGHTBOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective
9 Videos
- SEMICONDUCTORSBOOK - DC PANDEY ENGLISHCHAPTER - SEMICONDUCTORSEXERCISE - Subjective
12 Videos
Similar Questions
Knowledge Check
What is the refractive index of material of a plano-convex lens , if the radius of curvature of the convex surface is 10 cm and focal length of the lens is 30 cm ?
A65B74C23D43
The plane surface of a plano-convex lens of refracting index 1.5, is silvered. The radius of curvature of curved surface is R. Find the focal length of the mirror thus formed.
View SolutionLight is incident on the thin lens as shown in figure. The refractive index of the material of the lens is μ2. The radii of curvature of both the surfaces are R. The refractive index of the medium of left side is μ1, while that of right side is μ3. What is the focal length of the lens?

View SolutionA plano convex lens is made of glass of refractive index 1.5. The radius of curvature of its convex surface is R. Its focal length is
View SolutionFind the refractive index of the material of a plano-convex lens, if the radius of curvature of the convex surface is 20 cm and focal length of the lens is 60 cm?
View SolutionGiven figures shows the arrangement of two lenses. The radii of curvature of all the curved surfaces are same. The ratio of the equivalent focal length of combinations P,Q and R is:

View SolutionA biconvex lens (μ=1.5) has radius of curvature 20cm (both).
find its focal length.

View SolutionIf the radius of curvature is R, then the focal length is given by .........
View Solution