In the figure, masses m(1), m(2) and M are 20kg, 5kg, and 50kg respect

In the figure masses $m_{1}, m_{2}$ and M are kg. 20 Kg, 5 kg and 50 kg respectively. The co-efficient of friction between M and ground is zero. The co-efficient of friction between $m_{1}$ and M and that between $m_{2}$ and ground is $0.3 .$ The pulleys and the string are massless. The string is perfectly horizontal between $P_{1} and m_{1}$ and also between $P_{2} and m_{2} .$ The string is perfectly verticle between $P_{1} and P_{2} .$ An externam horizontal force F is applied to the mass M. Take $g = 10 m / s^{2} .$
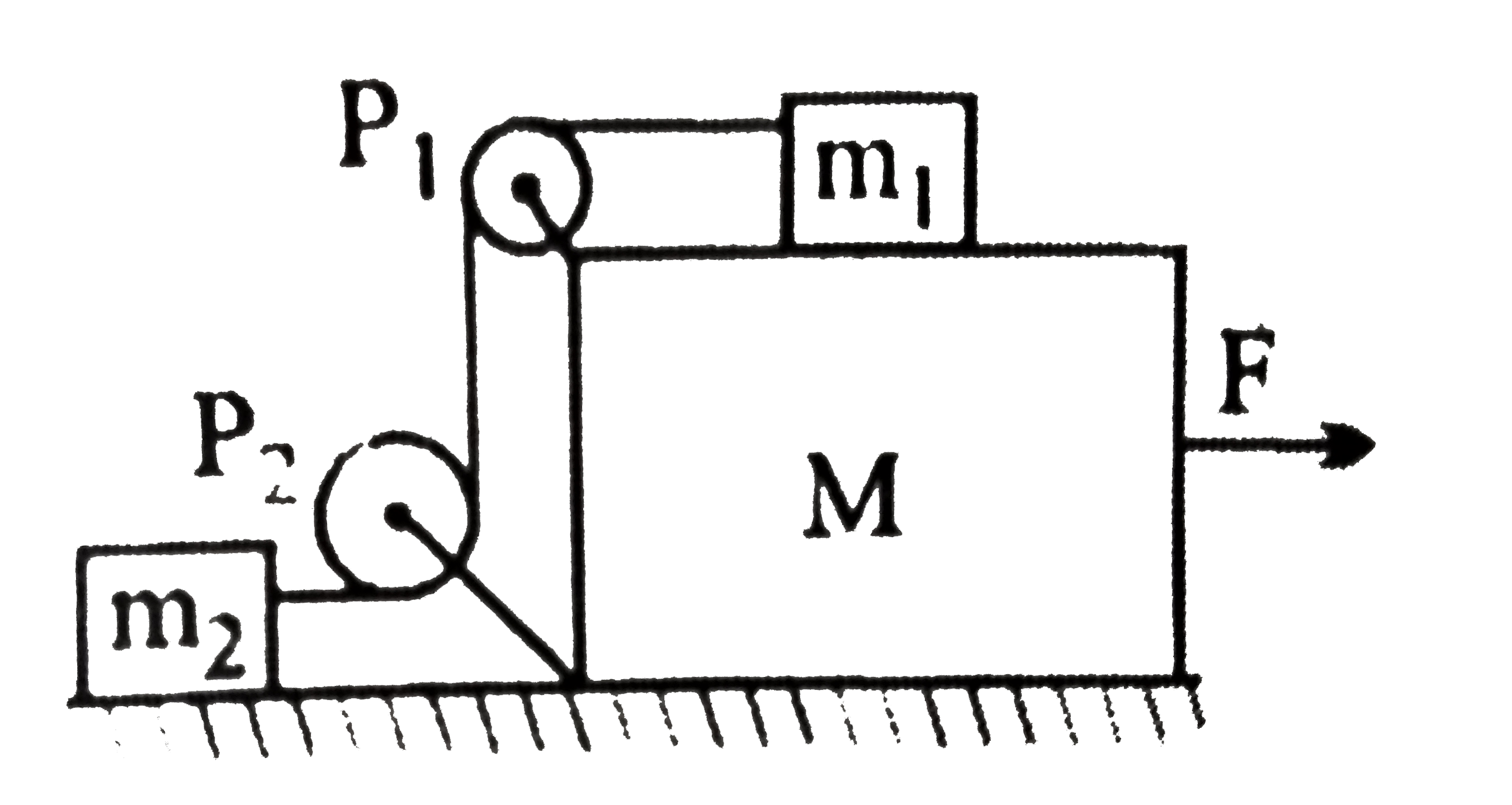
ocr_image
(i) Drew a free-body diagram for mass M, clearly showing all the forces.
(ii) Let the magnitude of the force of friction between $m_{1}$ and M be $f_{1}$ and that between $m,_{2}$ and ground be $f_{2} .$ For a particular F it is found that $f_{1} = 2 f_{2} .$ Find $f_{1} and f_{2} .$ Write down equations of motion of all the masses. Find F, tension in the string and accelerations of the masses.

View Solution

In the figure masses $m_{1}$ , $m_{2}$ and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between $m_{1}$ and M and that between $m_{2}$ and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between $P_{1}$ and $m_{1}$ and also between $P_{2}$ and $m_{2}$ . The string is perfectly vertical between $P_{1}$ and $P_{2}$ . An external horizontal force F is applied to the mass M. Take $g = 10 m / s^{2}$ .
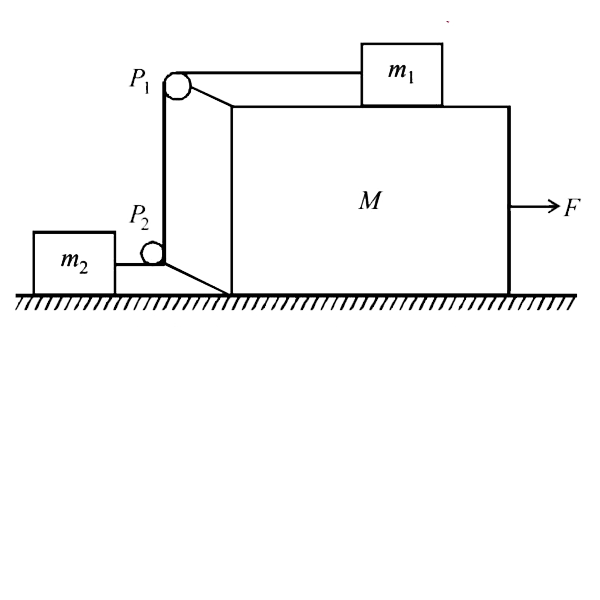
ocr_image
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between $m_{1}$ and M be $f_{1}$ and that between $m_{2}$ and ground be $f_{2}$ . For a particular F it is found that $f_{1} = 2 f_{2}$ . Find $f_{1}$ and $f_{2}$ . Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.

View Solution

In the figure masses $m_{1}$ , $m_{2}$ and M are 20 kg, 5kg and 50kg respectively. The coefficient of friction between M and ground is zero. The coefficient of friction between $m_{1}$ and M and that between $m_{2}$ and ground is 0.3. The pulleys and the strings are massless. The string is perfectly horizontal between $P_{1}$ and $m_{1}$ and also between $P_{2}$ and $m_{2}$ . The string is perfectly vertical between $P_{1}$ and $P_{2}$ . An external horizontal force F is applied to the mass M. Take $g = 10 m / s^{2}$ .
ocr_image
(a) Draw a free body diagram for mass M, clearly showing all the forces.
(b) Let the magnitude of the force of friction between $m_{1}$ and M be $f_{1}$ and that between $m_{2}$ and ground be $f_{2}$ . For a particular F it is found that $f_{1} = 2 f_{2}$ . Find $f_{1}$ and $f_{2}$ . Write equations of motion of all the masses. Find F, tension in the spring and acceleration of masses.

View Solution

When force F applied on $m_{1}$ and there is no friction between $m_{1}$ and surface and the coefficient of friction between $m_{1} and m_{2}$ is $μ .$ What should be the minimum value of F so that there is on relative motion between $m_{1} and m_{2}$
ocr_image

View Solution

Two blocks of masses $m_{1}$ and $m_{2}$ are placed in contact with each other on a horizontal platform as shown in figure The coefficent of friction between $m_{1}$ and platform is $2 μ$ and that between block $m_{2}$ and platform is $μ$ .The platform moves with an acceleration $a$ . The normal reation between the blocks is
ocr_image

View Solution

A two block system is shown in figure . We shall draw complete free body diagram and find normal reaction between $m_{1} and m_{2}$ and between $m_{2}$ and ground .
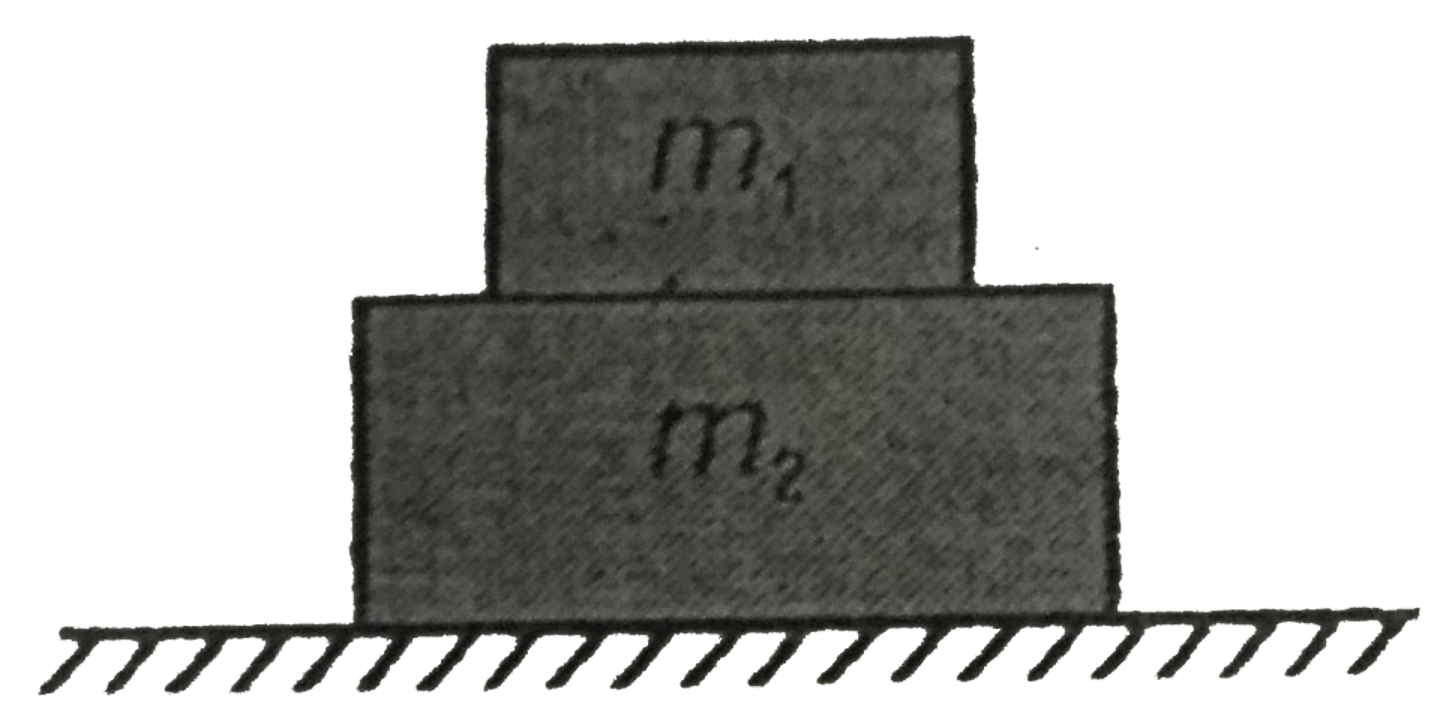
ocr_image

View Solution

In fig. both pulleys and the string are massless and all the surfaces are frictionless.
ocr_image
Given $m_{1} = 1 k g, m_{2} = 2 k g, m_{3} = 3 k g$ .
Find the tension in the string

View Solution

In fig. both pulleys and the string are massless and all the surfaces are frictionless.
ocr_image
Given $m_{1} = 1 k g, m_{2} = 2 k g, m_{3} = 3 k g$ .
The acceleration of $m_{1}$ is

View Solution

In fig. both pulleys and the string are massless and all the surfaces are frictionless.
ocr_image
Given $m_{1} = 1 k g, m_{2} = 2 k g, m_{3} = 3 k g$ .
The acceleration of $m_{3}$ is

View Solution

If coeffiecient of friction between the block of mass 2kg and table is 0.4 then out acceleration of the system and tension in the string. $(g = 10 m / s^{2})$
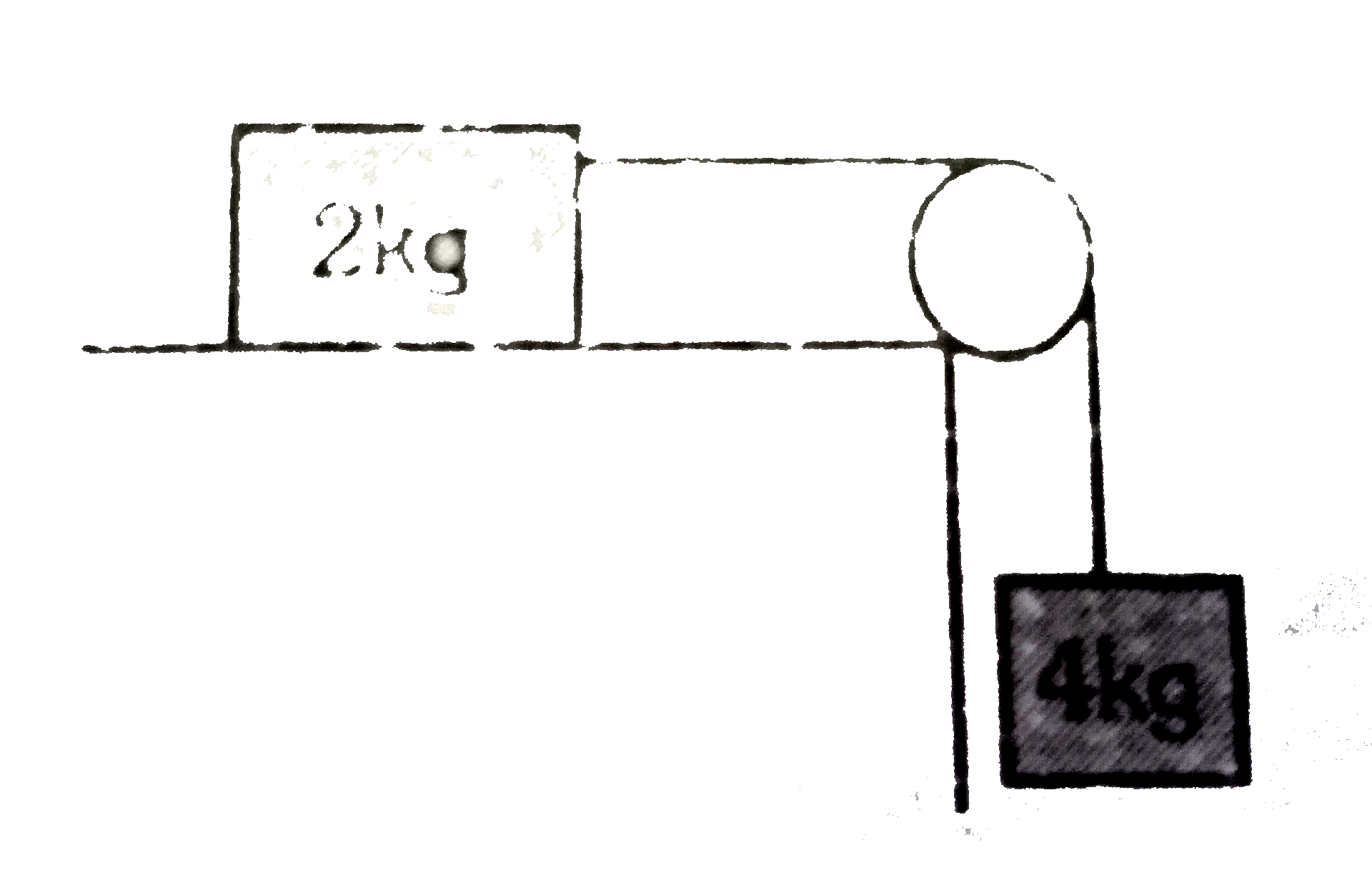
ocr_image

View Solution

The correct Answer is:A

Topper's Solved these Questions

Similar Questions

AAKASH SERIES-LAWS OF MOTION-EXERCISE - I