In the figure shown, A and B are two short steel rods each of cross-sectional area 5cm2. The lower ends of A and B are welded to a fixed plate CD. The upper end of A is welded to the L-shaped piece EFG, which can slide without friction on upper end of B. A horizontal pull of 1200N is exerted at G as shown. Neglect the weight of EFG.
Longitudinal stress in A is
(a)tensile in nature and having magnitude 180N/m2
(b)tensile in nature and having magnitude 240N/m2
(c)compressive in nature and having magnitude 180N/m2
(d)compressive in nature and having magnitude 240N/m2
The correct Answer is:A
To solve the problem, we need to determine the longitudinal stress in rod A when a horizontal pull of 1200 N is exerted at point G.
1. Identify the Forces Acting on the System:
- There is a horizontal pull of 1200 N at point G.
- Let N1 be the force in rod A and N2 be the force in rod B.
2. Establish Equilibrium Conditions:
- Since the system is in equilibrium, the sum of vertical forces must equal zero:
N1=N2
3. Torque Equilibrium:
- We can analyze the torques about point E to find the relationship between N2 and the applied force.
- The distance from E to C (where rod B is fixed) is 4 cm, and the distance from G to F is 3 m (or 300 cm).
- The torque due to N2 is:
Torque due to N2=N2×4 cm
- The torque due to the applied force (F) is:
Torque due to F=1200 N×300 cm
- Setting these equal for rotational equilibrium:
N2×4=1200×300
4. Solve for N2:
- Rearranging gives:
N2=1200×3004
- Calculate N2:
N2=3600004=90000 N
5. Determine the Longitudinal Stress in Rod A:
- The longitudinal stress σA in rod A is given by:
σA=N1A
- Since N1=N2, we have:
σA=90000 NA
- The cross-sectional area A is given as 5 cm2 (which is 5×10−4 m2).
- Therefore:
σA=900005×10−4=180000000 N/m2=180 N/cm2
6. Conclusion:
- The longitudinal stress in rod A is 180 N/cm2 and is tensile in nature.
Final Answer:
The longitudinal stress in rod A is 180 N/cm2 (tensile).
- There is a horizontal pull of 1200 N at point G.
- Let N1 be the force in rod A and N2 be the force in rod B.
- Since the system is in equilibrium, the sum of vertical forces must equal zero:
N1=N2
- We can analyze the torques about point E to find the relationship between N2 and the applied force.
- The distance from E to C (where rod B is fixed) is 4 cm, and the distance from G to F is 3 m (or 300 cm).
- The torque due to N2 is:
Torque due to N2=N2×4 cm
- The torque due to the applied force (F) is:
Torque due to F=1200 N×300 cm
- Setting these equal for rotational equilibrium:
N2×4=1200×300
- Rearranging gives:
N2=1200×3004
- Calculate N2:
N2=3600004=90000 N
- The longitudinal stress σA in rod A is given by:
σA=N1A
- Since N1=N2, we have:
σA=90000 NA
- The cross-sectional area A is given as 5 cm2 (which is 5×10−4 m2).
- Therefore:
σA=900005×10−4=180000000 N/m2=180 N/cm2
- The longitudinal stress in rod A is 180 N/cm2 and is tensile in nature.
The longitudinal stress in rod A is 180 N/cm2 (tensile).
Topper's Solved these Questions
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Integer
Explore 6 Videos
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Fill In The Blanks
Explore 1 Video
- PROPERTIES OF SOLIDS AND FLUIDSBook:CENGAGE PHYSICS ENGLISHChapter:PROPERTIES OF SOLIDS AND FLUIDSExercise:Assertion- Reasoning
Explore 13 Videos
- NEWTON'S LAWS OF MOTION 2Book:CENGAGE PHYSICS ENGLISHChapter:NEWTON'S LAWS OF MOTION 2Exercise:Integer type
Explore 1 Video
- RIGID BODY DYNAMICS 1Book:CENGAGE PHYSICS ENGLISHChapter:RIGID BODY DYNAMICS 1Exercise:Integer
Explore 11 Videos
Similar Questions
Four plates of the same area of cross-section are joined as shown in the figure. The distance each plate is d. The equivalent capacity across A and B will be

View SolutionA body of mass M is attached to the lower end of a metal wire, whose upper end is fixed . The elongation of the wire is l.
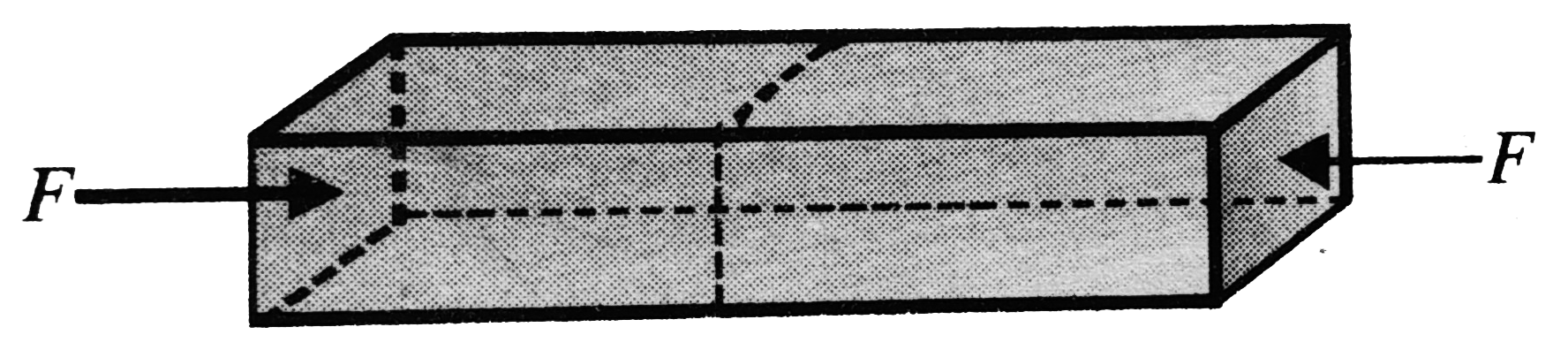
View SolutionIn the figure shown, forces of equal magnitude are applied to the two ends of a uniform rod. Consider A as the cross-sectional area of the rod. For this situation, mark out the incorrect statements.
View SolutionIn the figure shown, the spring are connected to the rod at one end and at the midpoint. The rod is hinged at its lower end. Rotational SHM of the rod (Mass m, length L) will occur only if-
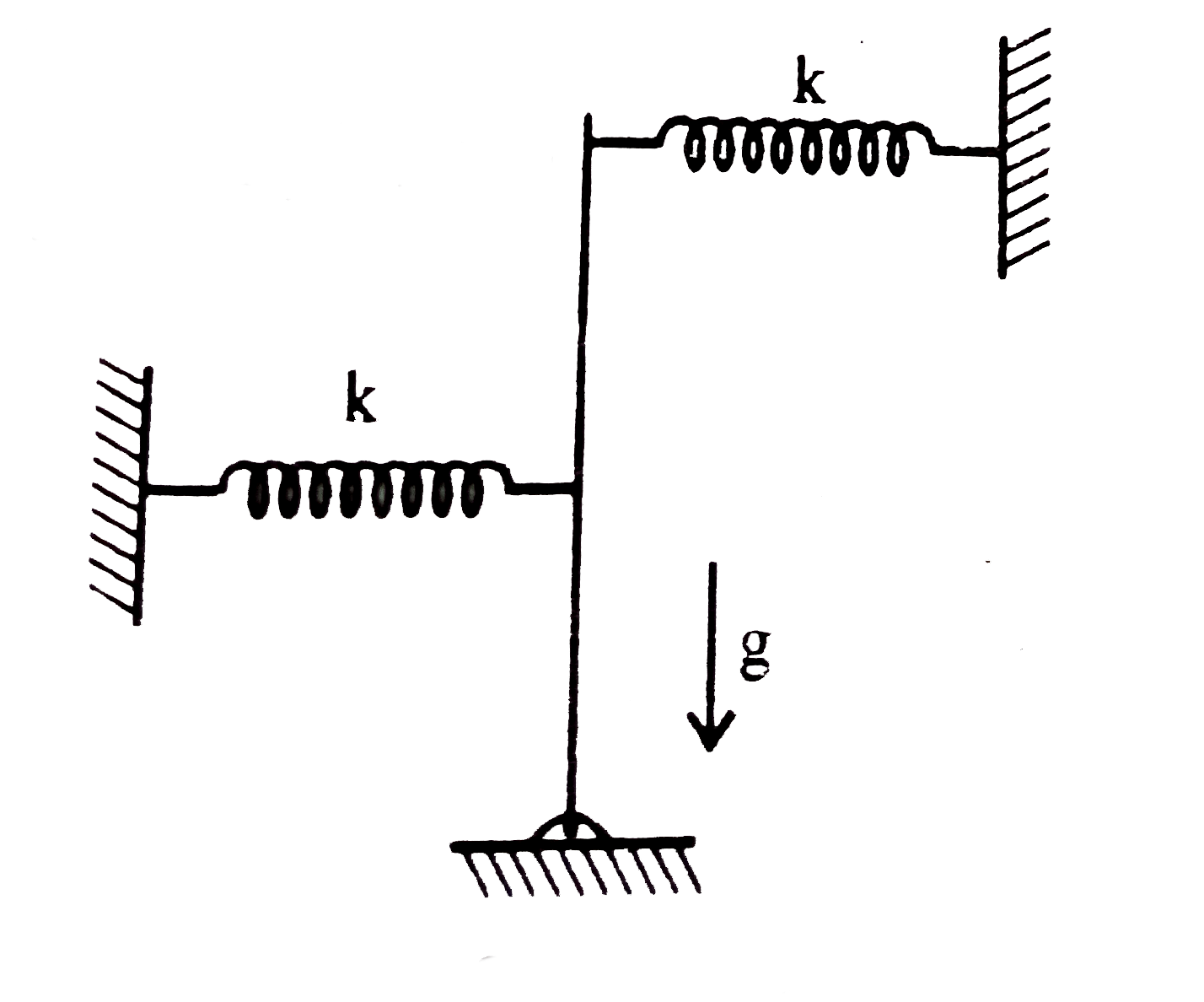
View SolutionA uniform cylindrical rod of length L and cross-sectional area by forces as shown in figure.

The elongation produced in the rod is
View SolutionA steel rod has a radius of cross-sectional area is R= 10 mm and length L = 90 cm ls fixed at one end, a force F=3.14⋅104N stretches it along its length, the stress in the rod is equal to (take π = 3.14)
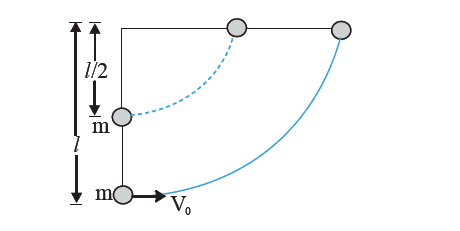
View SolutionA light rod of length l is pivoted at the upper end. Two masses (each m), are attached to the rod, one at the middle and the other at the free end. What horizontal velocity must be imparted to the lower end mass, so that the rod may just take up the horizontal position ?
View SolutionTwo rods A and B of same area of cross-section are joined together end to end The free end of the rod A is kept in melting ice at 300 K and free end of B rod at 400 K. The rods are of the same length. The conductivity of A is 3 times that of B. Calculate the temperature of the junction of the rods.
View SolutionEnd A of the bar AB in figure rests on a frictionless horizontal surface and end B is hinged. A horizontal force →F of magnitude 120N is exerted on end A. You can ignore the weight of the bar. What is the net force exerted by the bar on the hinge at B?

View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View Solution