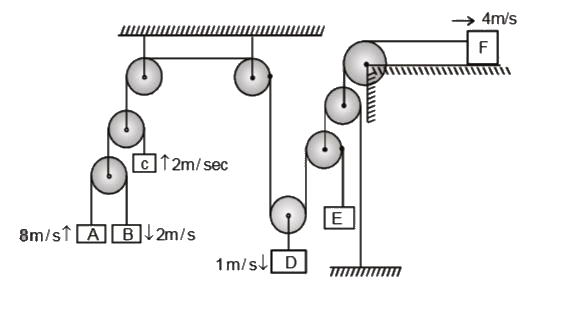
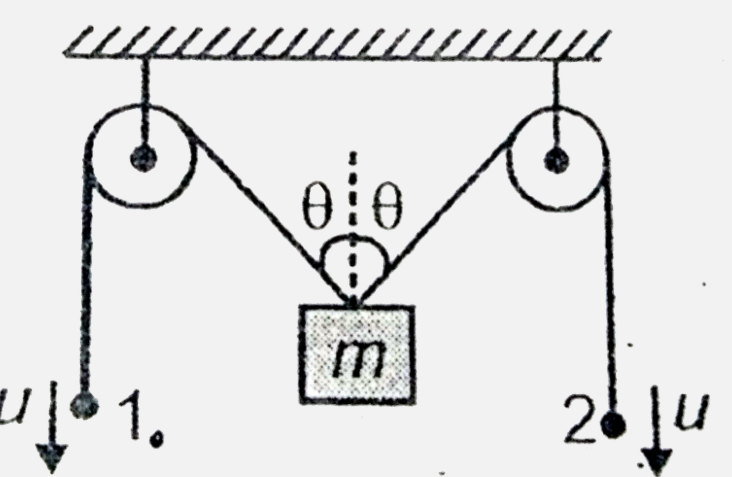
In the figure shown, the lower pulley is free to move in a vertical direction only. Block A is given a uniform velocity u as shown, what is the velocity of block B as a function of angle θ? 
ucosθ
ucosθ
u[1+sinθ]cosθ
u[1+cosθ]sinθ
The correct Answer is:C
Let in a small time dt, displacement of A is dx and displacement of B is dy. Increase in length l1=dx
Increase in the length l2=dxsinθ−dycosθ

But net increase in the length in the length should be zero, so
dx+dxsinθ−dycosθ=0
⇒dy=(1+sinθ)dxcosθ
=dydt=(1+sinθcosθ)dxdt
⇒v=(1+sinθcosθ)u
Topper's Solved these Questions
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - MCQ_TYPE
20 Videos
- MISCELLANEOUS VOLUME 2BOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS VOLUME 2EXERCISE - LC_TYPE
34 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICSCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
- NEWTON'S LAWS OF MOTION 1BOOK - CENGAGE PHYSICSCHAPTER - NEWTON'S LAWS OF MOTION 1EXERCISE - Integer
5 Videos
Similar Questions
Knowledge Check
In the figure shown the velocity of different blocks is shown. The velocity of C is
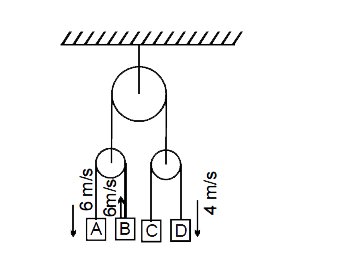 A6 m/sB4 m/sC0 m/sDnone of these
A6 m/sB4 m/sC0 m/sDnone of theseIf block A is moving horizontally with velocity vA, then find the velocity of block B at the instant as shown in fig.
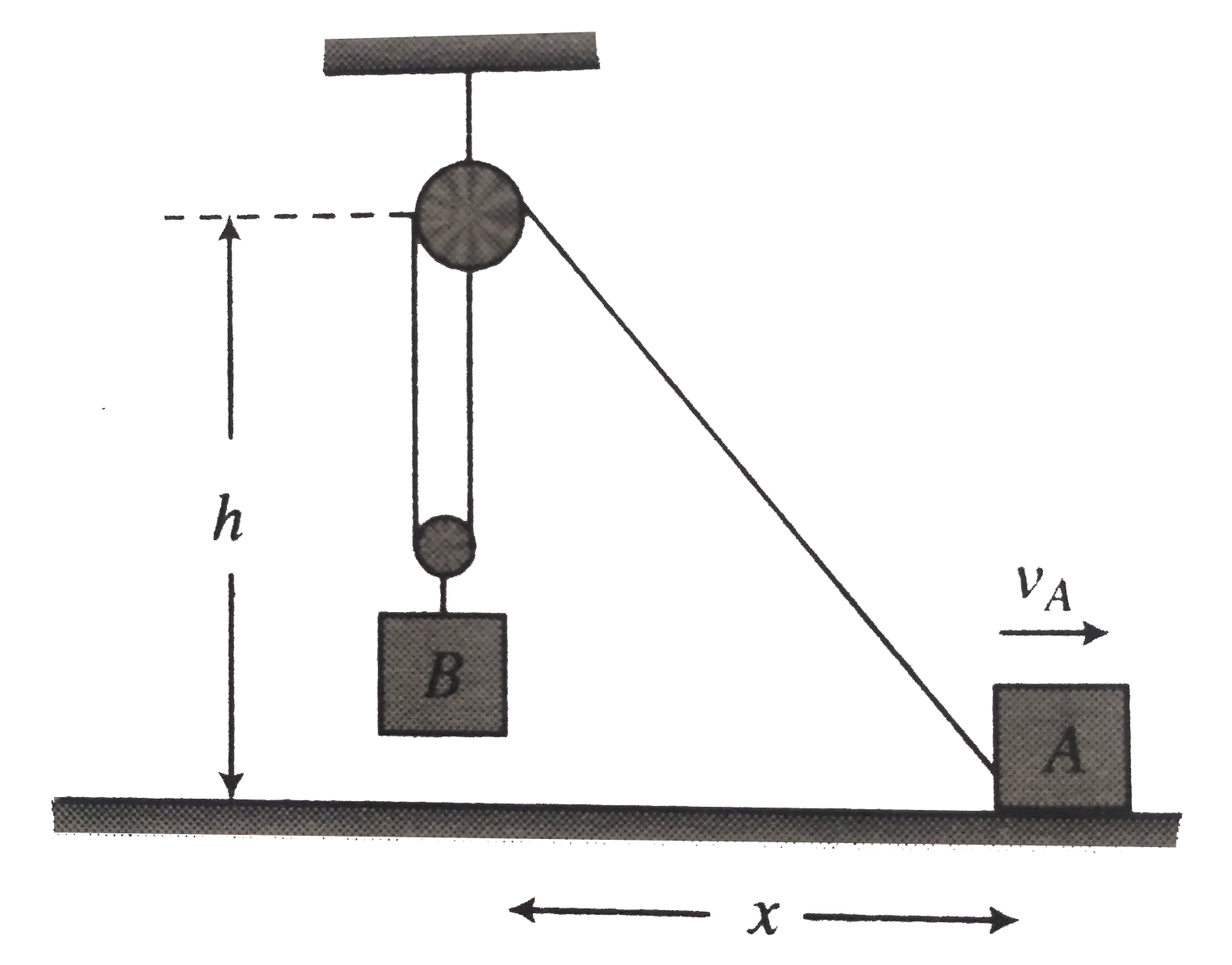 AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
AhvA2√x2+h2BxvA√x2+h2CxvA2√x2+h2DhvA√x2+h2
Find velocity of block 'B' at the instant shown in figure.
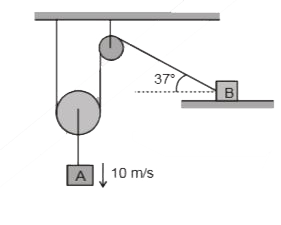
View SolutionFind velocity of block 'B' at the instant shown in figure :

View SolutionIn the figure shown the velocity of different blocks is shown. The velocity of C is

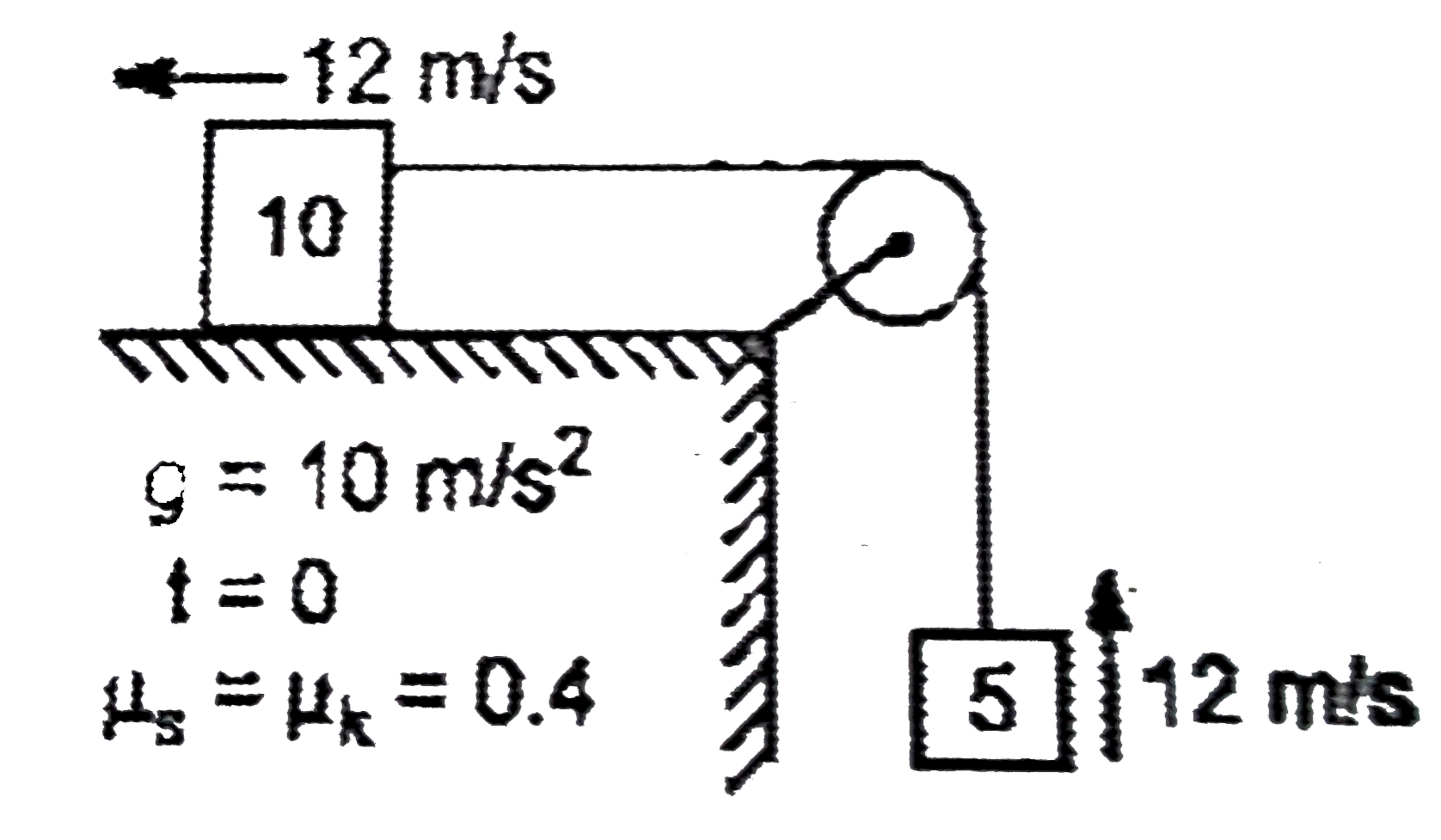
View SolutionBlocks are given velocities as shown at t=0, find velocity and position of 10 kg block at t=1 and t=4.
View SolutionIn the figure shown, the blocks A and B are connected with an inextensible string. If the block B is pulled with a velocity of 5 m/s then it is observed that block A moves with 10 m/s. Find the angle theta in (degree) shown in the diagram:
View SolutionIn the arrangement shown in figure if speed of point 1 and point 2 are u, then what is the velocity of block at given instant of time.
View Solution