In the figure shown, u=√6gR(>√5gR)
Find h,v,ar,at,T and Fnet when
(a) θ=60∘
(b) θ=90∘
(c) θ=180∘
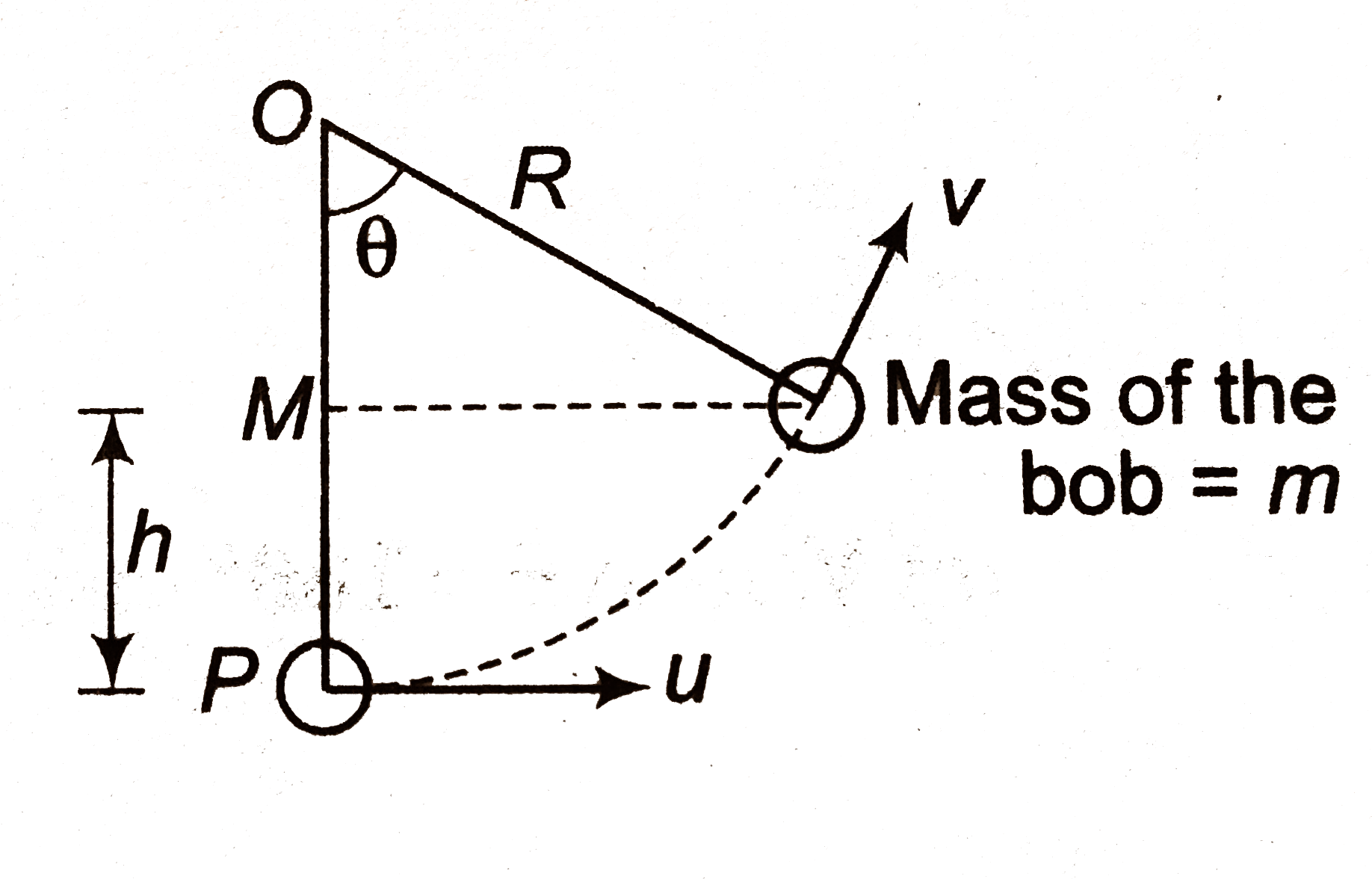
The correct Answer is:A, B
When θ=60∘

In the figure, we can see that,
h=PM=OP−OM=R−Rcosθ
=R−Rcos60∘=R−R2
v=√u2−2gh=√6gR−2g(R2)=√5gR
ar=v2R=(√5gR)2R=5g
at=Ftm=√3mg2m=√3g2
a=√a2r+a2t=
⎷(5g)2+(√g2)2=√1032g ltbr> T=mg2=mar=(5g)
T=5.5mg
Fnet=ma=√1032mg
(b) When θ=90∘
h=R
v=√u2−2gh=√6gR−2gR
=2√gR
ar=v2R=⎛⎜⎝2√gR2R⎞⎟⎠=4g
at=Ftm=mgm=g
a=√a2r+a2t=√(4g)2+(g)2=√17g
T=mar=m(4g)
=4mg
Fnet=ma
=√17mg
(c) Where θ=180∘
h=2R
v=√u2−2gh
=√6gR−2g×2R
=√2gR
ar=v2R=(√2gR)2R =2g
at=Ftm=0
a=ar
2g
T+mg=mar=m(2g)
T=mg

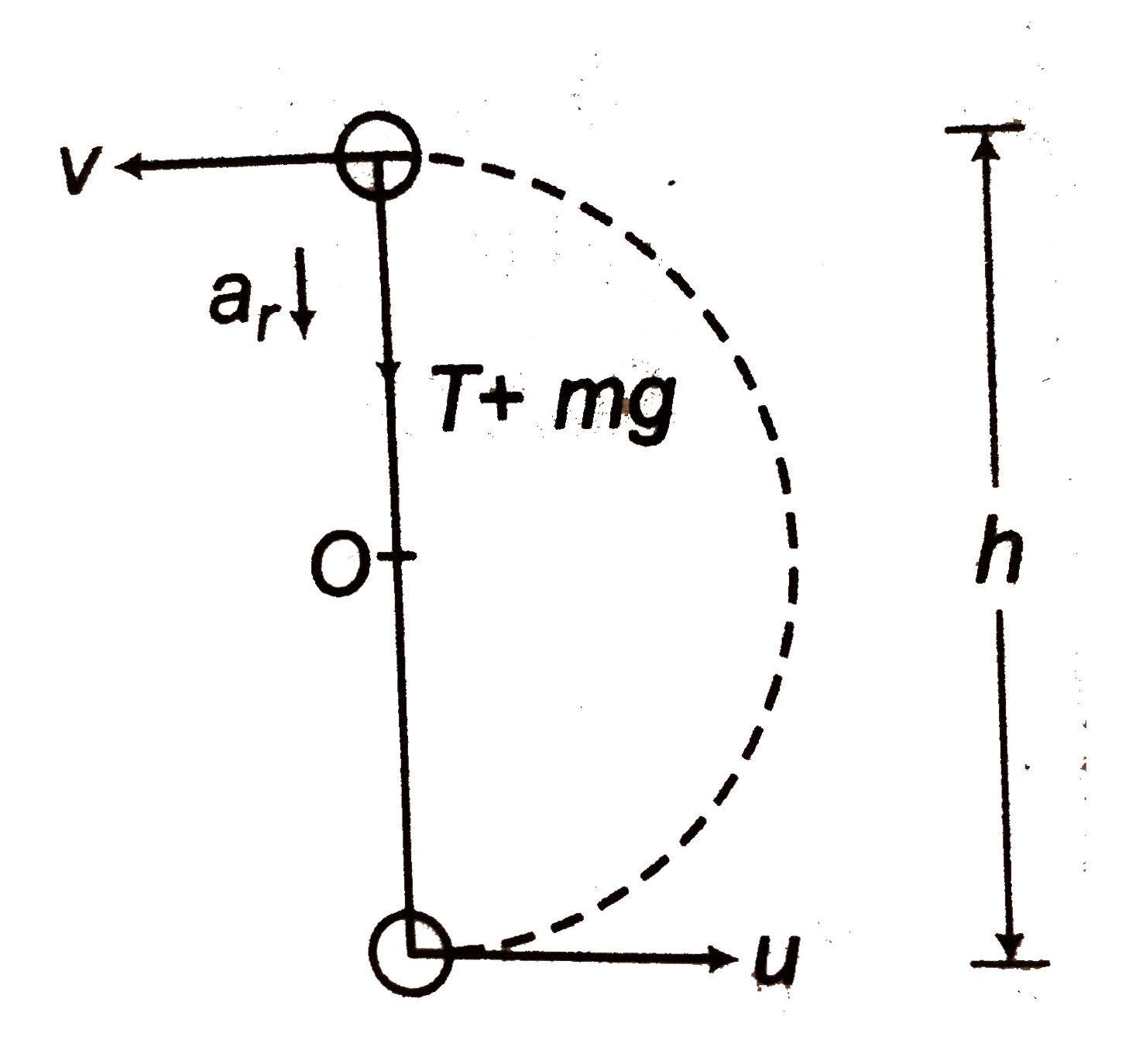
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Miscellaneous Examples
5 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Exercise 10.1
7 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Medical entrances s gallery
19 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
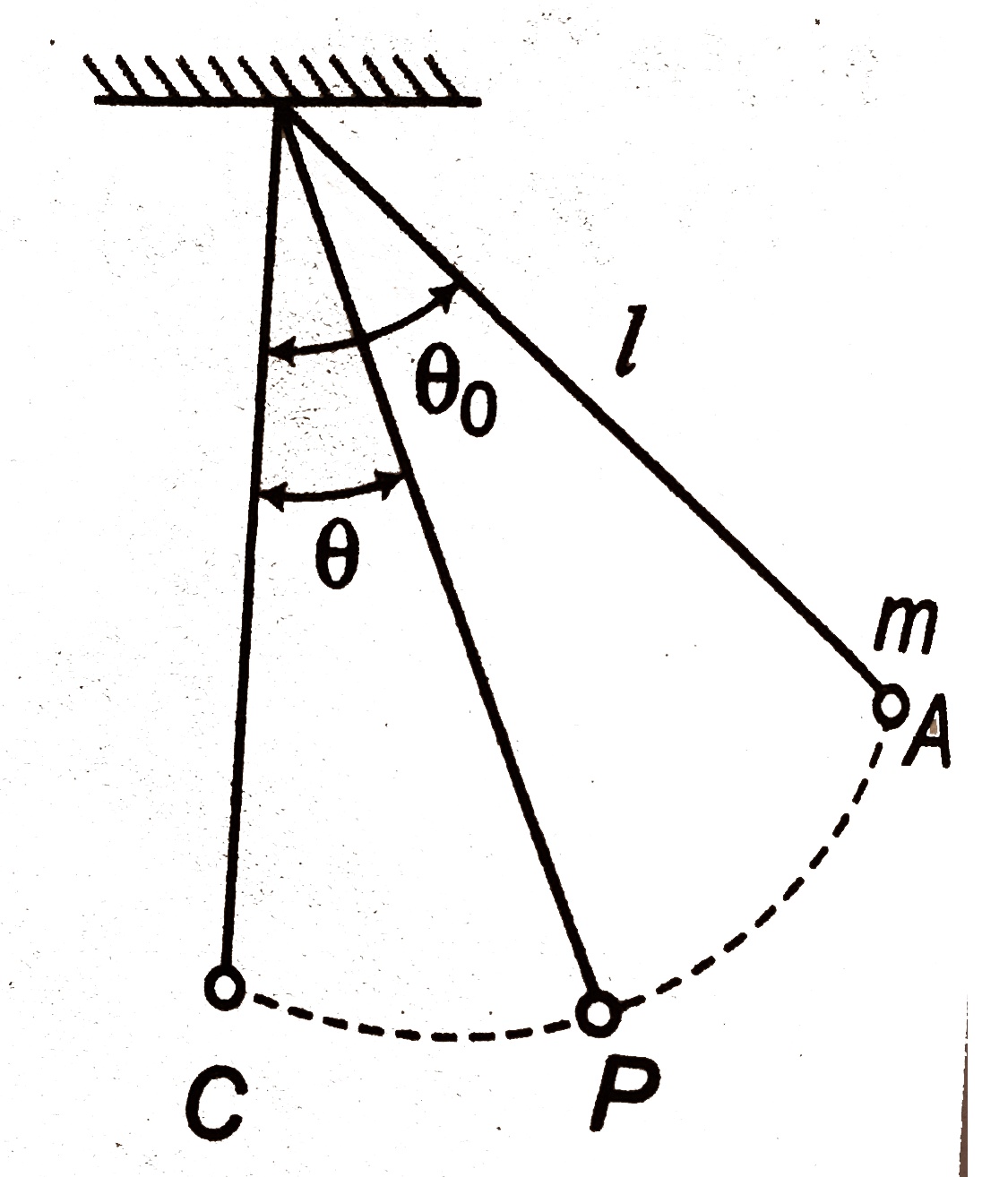
A ball of mass 'm' is released from point A where, Θ0=53∘ . Length of pendulum is 'l' . Find v,ar,at,a , T and Fnet at
(a) point A
(b) point C
(c) pont P where θ=37∘
View SolutionIn the figure shown, angle of repose is 45∘.Find force of friction, net force and acceleration of the block when
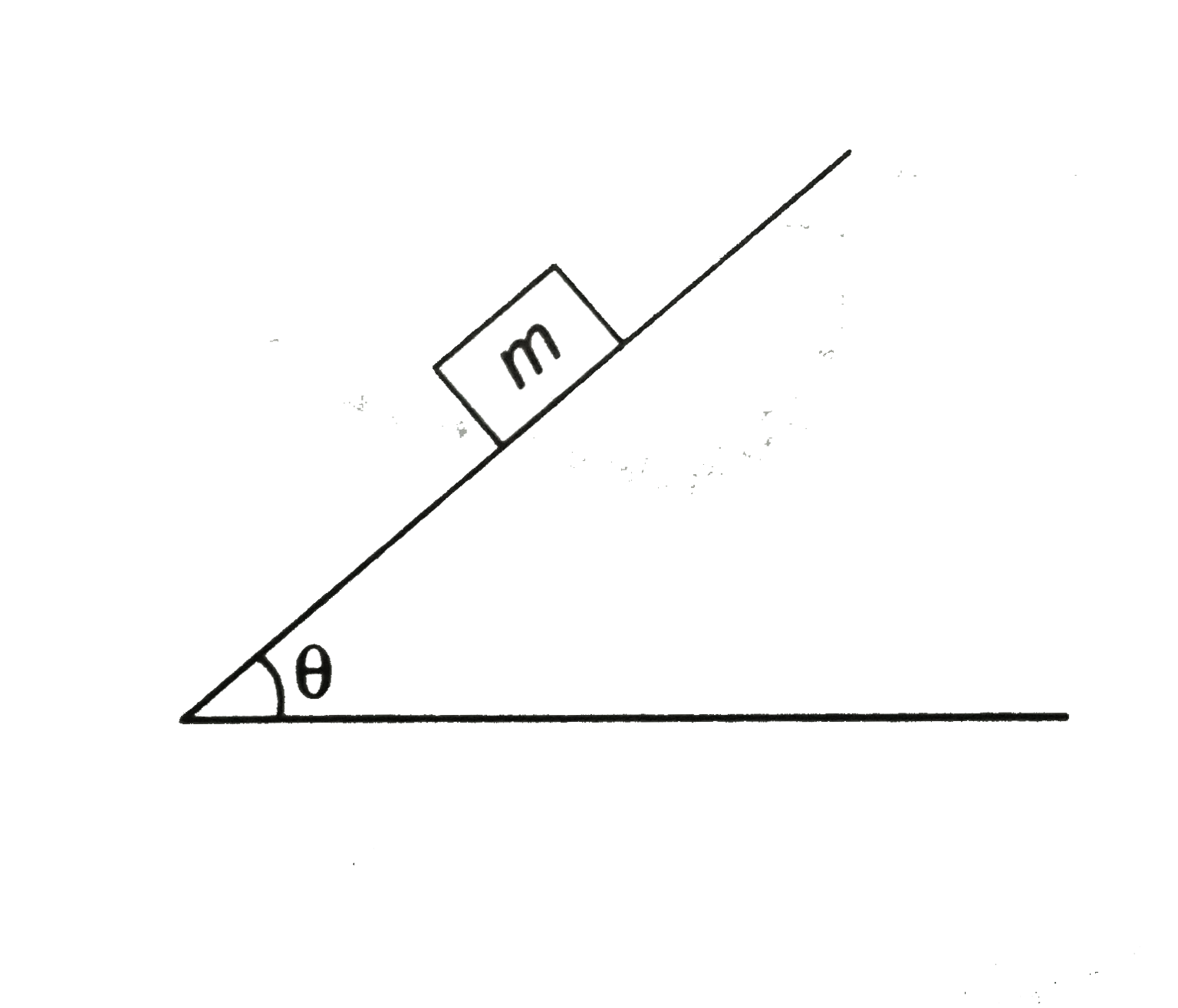
(a) θ=30∘ (b)θ=45∘ (c)θ=60∘
View Solution
Knowledge Check
Two particles are projected from the same point with the same speed at different angles θ1 and θ2 to the horizontal. If their respective times of flights are T1 and T2 and horizontal ranges are same then
a) θ1+θ2=90∘ ,
b)T1=T2tanθ1
c.T1=T2tanθ2 ,
d) T1sinθ2=T2sinθ1Aa,b,dare correctBa,c,dare correctCb,c,dare correctDa,b,care correctIf θ is an acute angle such that 4sin2θ−2(√3+1)sinθ+√3=0, then: theta=
A30∘or60∘B45∘or90∘C0∘or180∘Dnone of theseIf θ is an acute angle such that 2sin2θ−2√2⋅sinθ+1=0,then:θ=A)30∘ B)45∘ C)60∘ D)90∘
A30∘B45∘C60∘D90∘
Consider two plane mirrors inclined at an angle θ as shown in figure. Find the number of object O formed these mirror when

(i)θ=60∘
(ii) θ=72∘ and the object at 40∘ from M1
(iii) θ=72∘ and the object is at 36∘ from M1
(iv) θ=80∘
View SolutionIn four situations, a rotating body has angular position θ(t) given by (a) θ=3t−4, (b) θ=−5t3+4t2+6, ( c) θ=2/t2−4/t, and (d) θ=5t2−3. To which situations do the angular equations of Table 10-1 apply?
View SolutionIn the above question if VS(t)=220√2sin(2π50t), find (a)l(t) ,(b)vR and (c )vC(t)
View SolutionIn the previous problem ,find the magnitude of change in velocity if (a) 90∘<θ<180∘ , (b) 180∘<θ<270∘ and (c ) 270∘<θ<360∘.
View SolutionFind the values of all the the T-Rations if :-
(a)costˆa=725 (b)sinθ=513
View Solution
