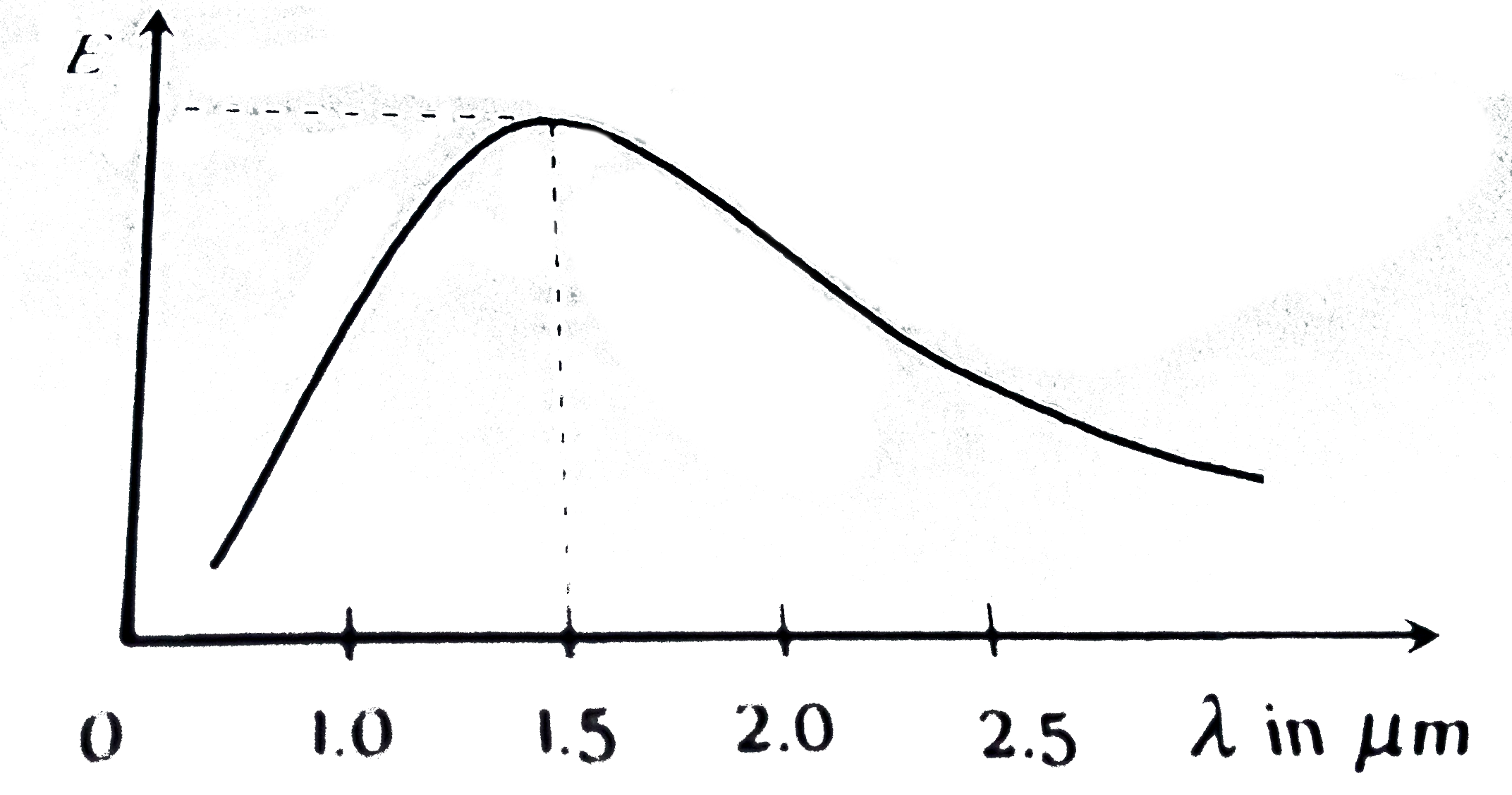
In the figure, the distribution of energy density of the radiation emitted by a black body at a given temperature is shown. The possible temperature of the black body is
A
1500 K
B
2000 K
C
2500 K
D
3000 K
Video Solution
Text Solution
The correct Answer is:B
λmT=b, where b = 2.890×10−3mK
⇒T=bλm = (2.89 xx 10^(-3))/(1.5 xx 10^(-6)) = 2000K
|
Topper's Solved these Questions
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Taking it together
47 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Assertion and reason
17 Videos
- CALORIMETRY AND HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY AND HEAT TRANSFEREXERCISE - Check points 16.3
20 Videos
- CALORIMETRY & HEAT TRANSFERBOOK - DC PANDEYCHAPTER - CALORIMETRY & HEAT TRANSFEREXERCISE - Level 2 Subjective
14 Videos
- CENTRE OF MASSBOOK - DC PANDEYCHAPTER - CENTRE OF MASSEXERCISE - Medical entrances gallery
27 Videos
Similar Questions
Knowledge Check
A black body emits
Aradiations of all wave lenghtsBno radiationCradiation of single wave lengthDradiation of selected wave lengthThe radiation emitted by a perfectly black body is proportional to
Aabsolute temperatureBfourth root of absolute temperatureCfourth power of absolute temperatureDsquare of absolute temperatureThe gross radiation emitted by a perfectly black body is:
ADependent on its temperatureBDependent on the area of its surfaceCDependent on the temperature of the surroundingsDIndependent of the temperature of the surroundings
If a black body is heated at a high temperature, it seems to be
View SolutionIf a black body is heated at a high temperature, it seems to be
View SolutionIf a black body is heated at a high temperature, it seems to be
View SolutionA black body at high temperature emits thermal radiations of
View SolutionThe amount of radiation emitted by a perfectly black body is proportional to .
View Solution
