In the given circuit, it is observed that the current I is independent of the value of the resistance R6. Then the resistance values must satisfy
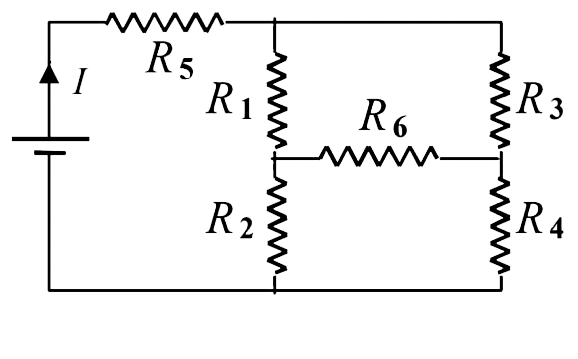 .
.
R1R2R5=R3R4R6
1R5+1R6=1R1+R2+1R3+R4
R1R4=R2R3
R1R3=R2R4=R5R6
The correct Answer is:C
c. Since current I is independent of R6, it follows that the
resistances R1,R2,R3,andR4 must form a balanced Wheatstone
bridge.
Similar Questions
Value of the resistance R in the figure is
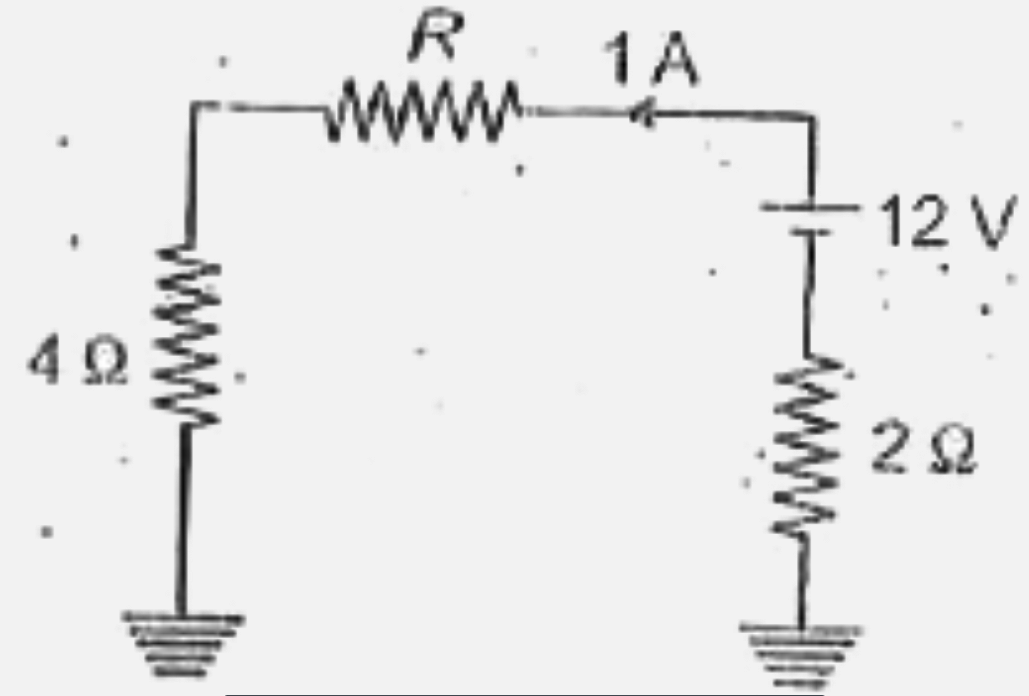 View Solution
View SolutionValue of the resistance R in the figure is
View SolutionIn the given circuit , the value of current is
 View Solution
View SolutionIn the circuit given below, the value of the current is
 View Solution
View SolutionIn the given circuit, if the potential difference across the internal resistance r1 is equal to E, then the resistance R is equal to:
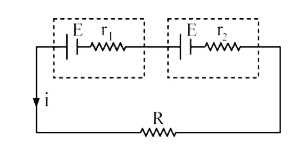 View Solution
View SolutionIn the given circuit, the resistances are given in ohm. The current through the 10Ω resistance is 3 A while that through the resistance X is 1 A. No current passes through the galavanometer. The values of the unknown resistances X and Y are respectively (in ohm)
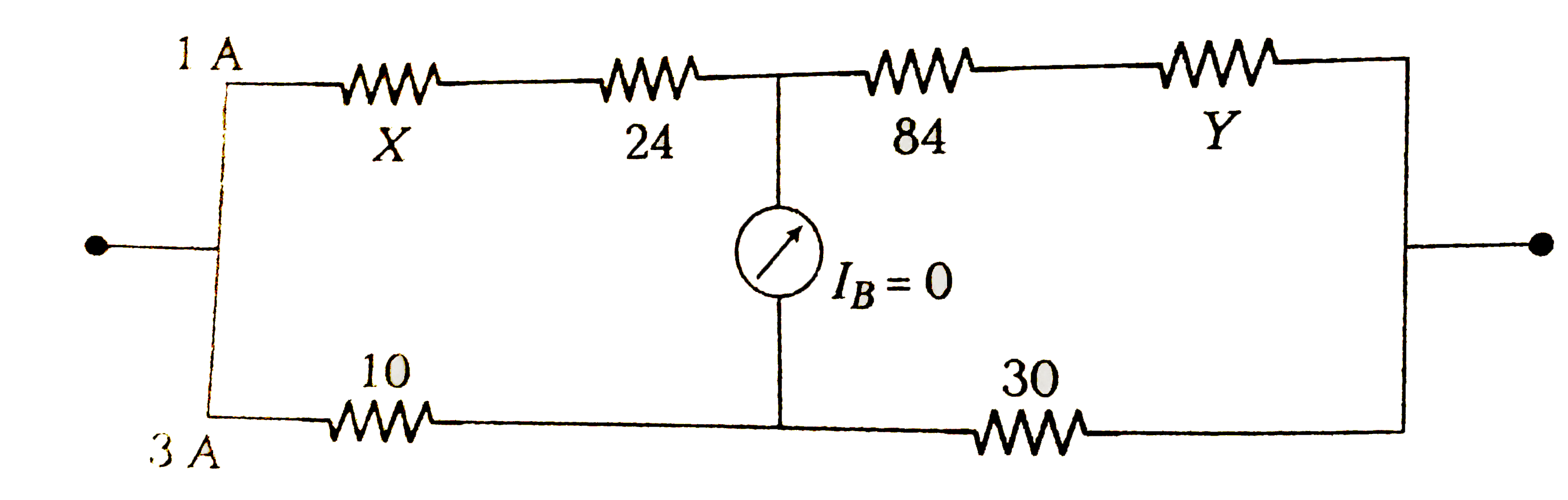 View Solution
View SolutionStatement I : In the circuit in Fig.7.46, both cells are ideal and of fixed emf, the resistor R1 has fixed resistance and the resistance of resistor R2 can be varied ( but R2 is always non zero). Then the electric power delivered to the resistor of resistance R1 is independent of the value of resistance R2.
Statement II: If potential difference across a fixed resistance is unchanged , the poweer delivered to the resistor remains constant.
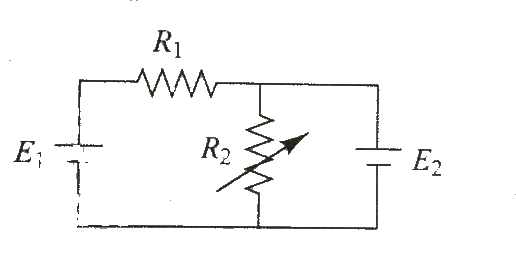 View Solution
View SolutionIn the given circuit, the current through the resistance R is __________ A.
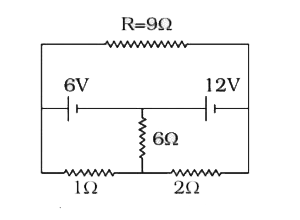 View Solution
View SolutionIf the ammeter in given circuit reads 1 A, then resistance R is
View SolutionIn the following circuit the current in each resistance is
 View Solution
View Solution



