In the given circuit, with steady current, the potential drop across the capacitor must be

V
V/2
V/3
2V/3
The correct Answer is:C
c. Method I: There will be no current flowing in branch BE
in steady condition. Let I be the current flowing in the loop
ABCDEFA. Applying Kirchhoff's law in the loop moving in
anticlockwise direction starting from C+
2V−I(2R)−I(R)−V=0orV=3IRorI=V/3R.
Applying Kirchhoff's law in the
circuit ABEF/A we get on moving
in anticlockwise direciton starting
form B
+V+V∩−IR−V=0
where V∩ is the potential
difference across capacitor
V∩=IR=V3R×R=V3
 .
.
Method II:
let us consider A to be
at OV. Then points B,
C, and D will be at V, V,
and 2 V, respectively. Let
the current be flowing in
the clockwise direction.
Applying Kirchhoff's law
in the outer loop, we get
V−IR−I(2R)−2V=0orI=−V/3R.
The minus sign here indicates that the current is in the opposite
direction to what we have assumed. Applying Kirchhoff's law
from A to E via B, we get
VA+V+IR=VE
or 0+V+V3R×R=VE=4V3
Again applying Kirchhoff's law from A to E via C, we get
VA+V+V∩=VCorV∩=V3
Similar Questions
In the given circuit, with steady current, the potential difference across the capacitor is
 View Solution
View SolutionIn the given circuit, with steady current, the potential of point A must be
 View Solution
View SolutionIn the given circuit, with steady current, calculate the potential difference across the capacitor and the charge stored in it.
View SolutionFind the potential drop across the capacitor in the given circuit.
 View Solution
View SolutionThe potential drop across 7μF capacitor is 6V. Then
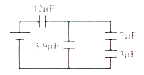 View Solution
View SolutionThe potential drop across the 3Ω resistor is
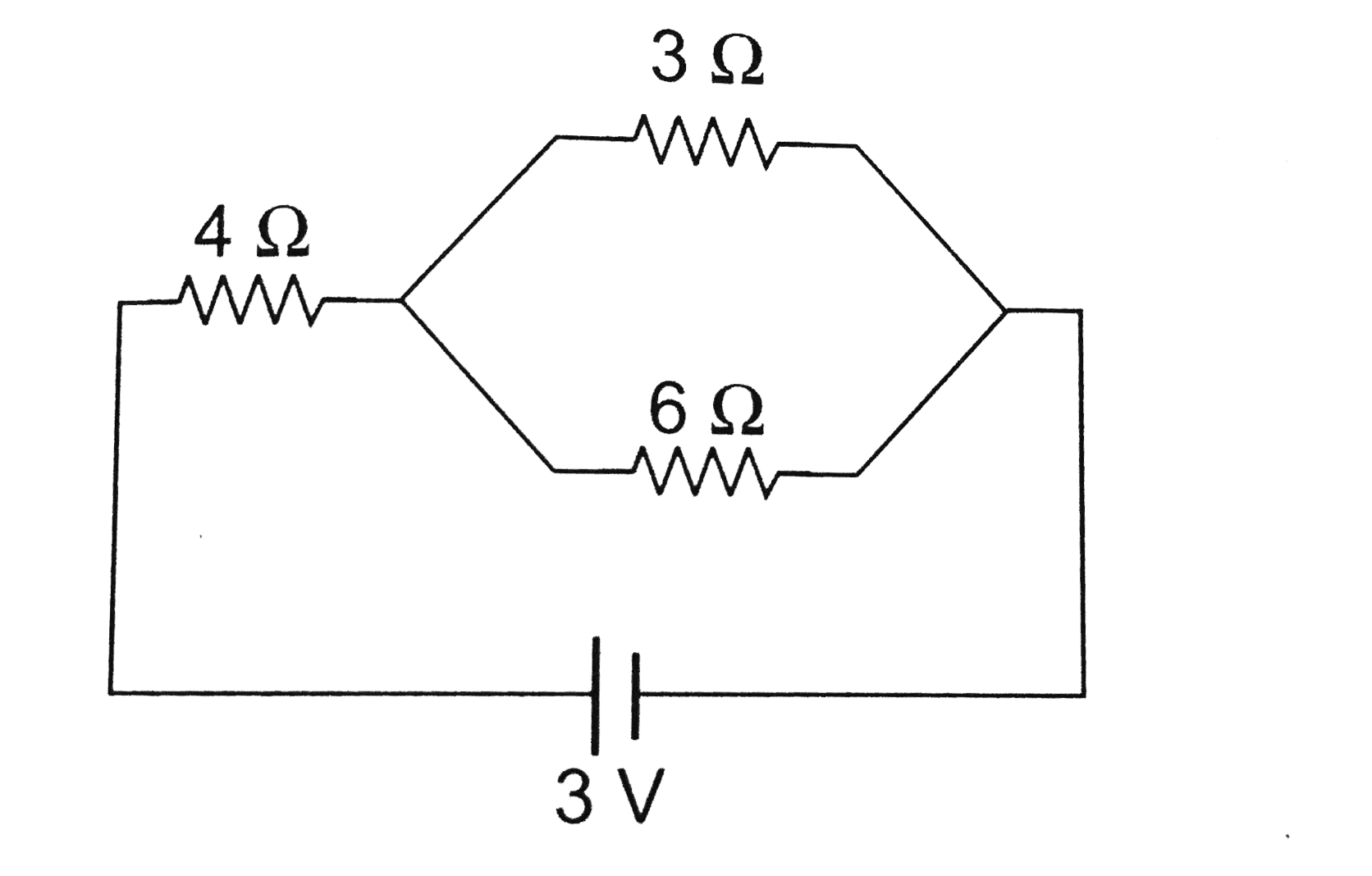 View Solution
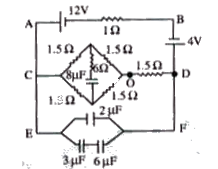
View SolutionIn the given circuit, find the potential differece across the 6μf capacitor in steady state.
 View Solution
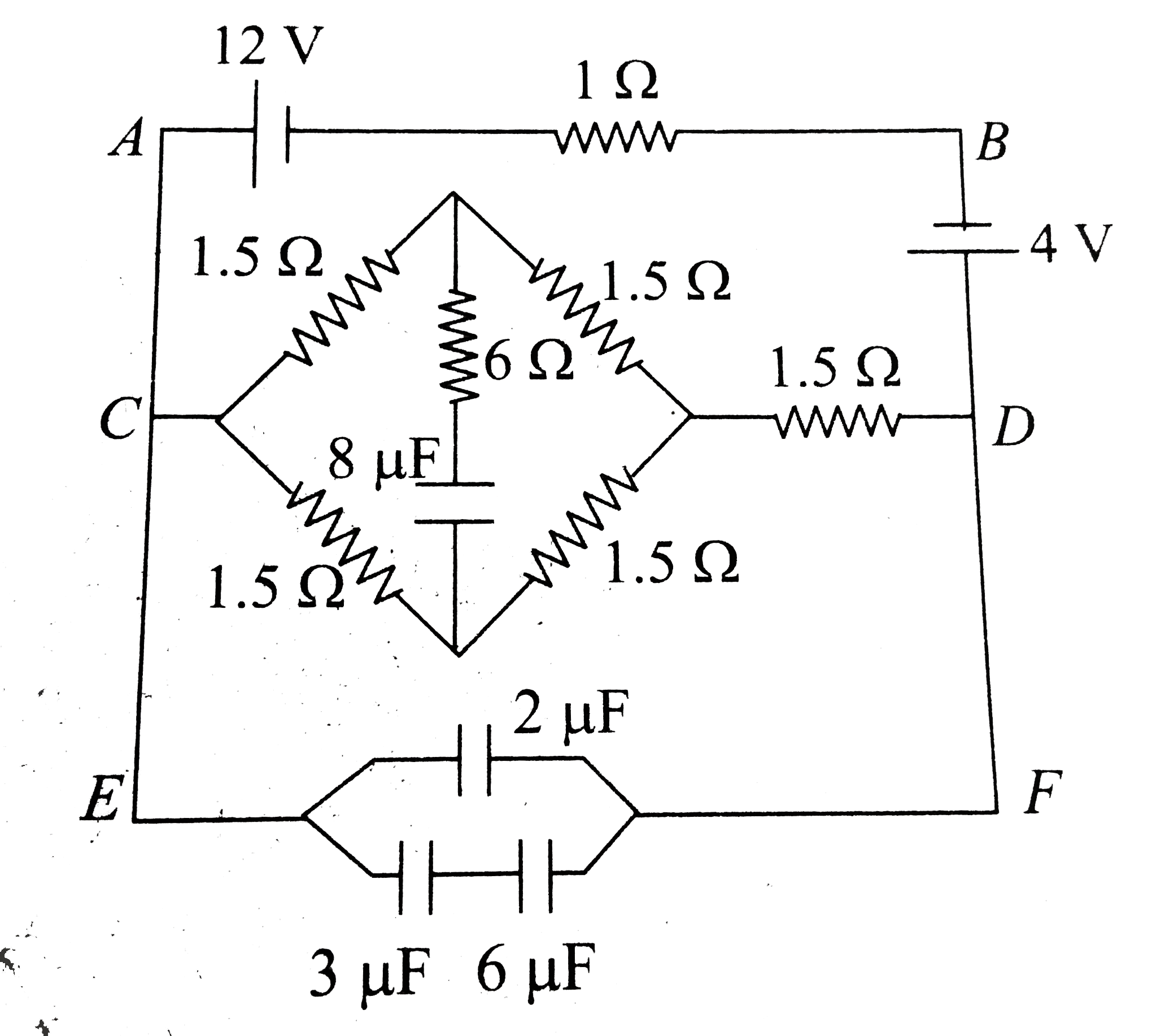
View SolutionIn the given circuit, the potential difference across the 6μF capacitor in steady state is
 View Solution
View SolutionIn the circuit shown in the figure, the potential difference across the 4.5μF capacitor is
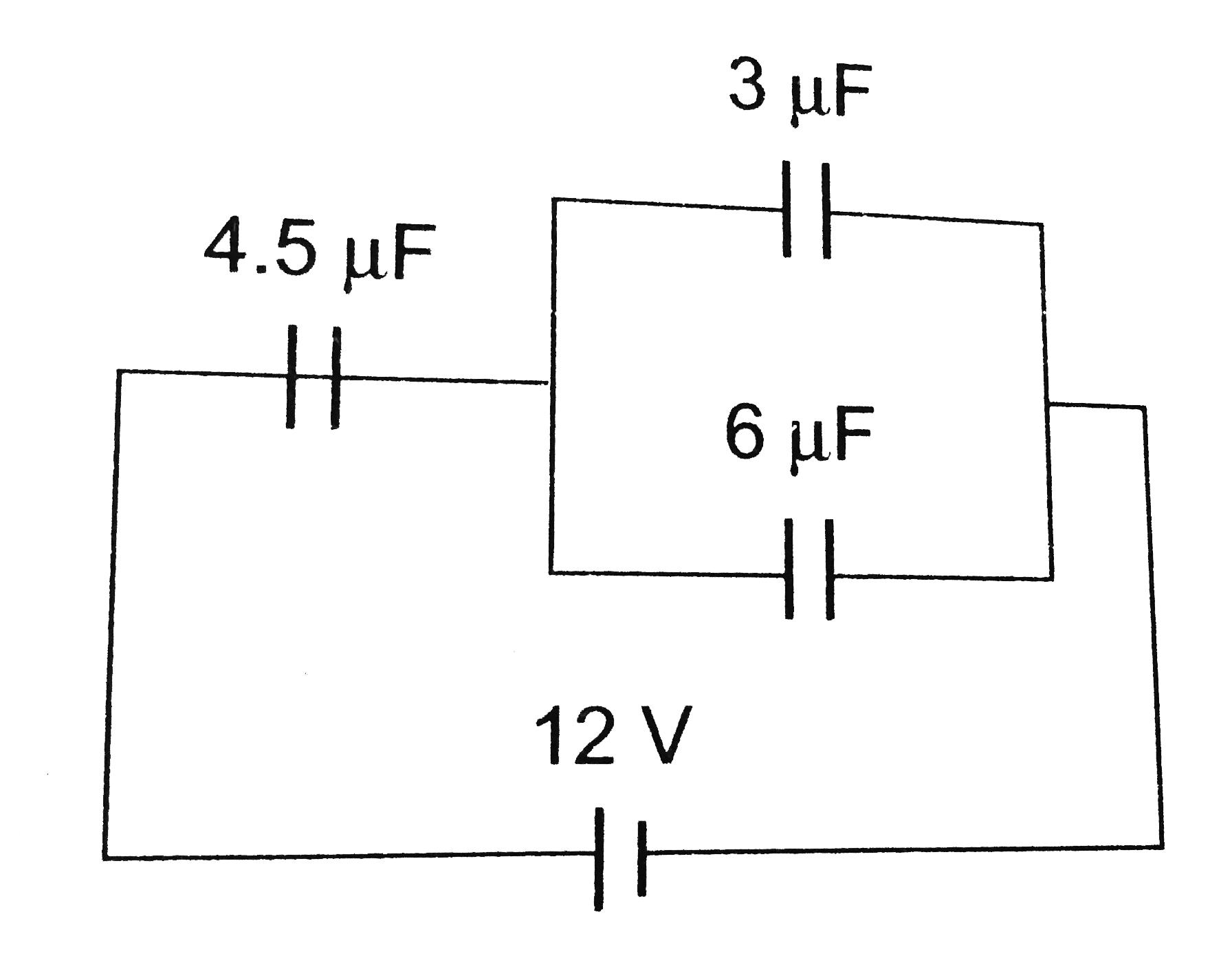 View Solution
View SolutionA resistor and a capacitor are connected in series with an a.c. source. If the potential drop across the capacitor is 5 V and that across resistor is 12 V, applied voltage is
View Solution

