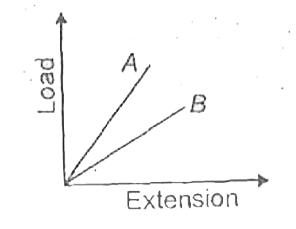
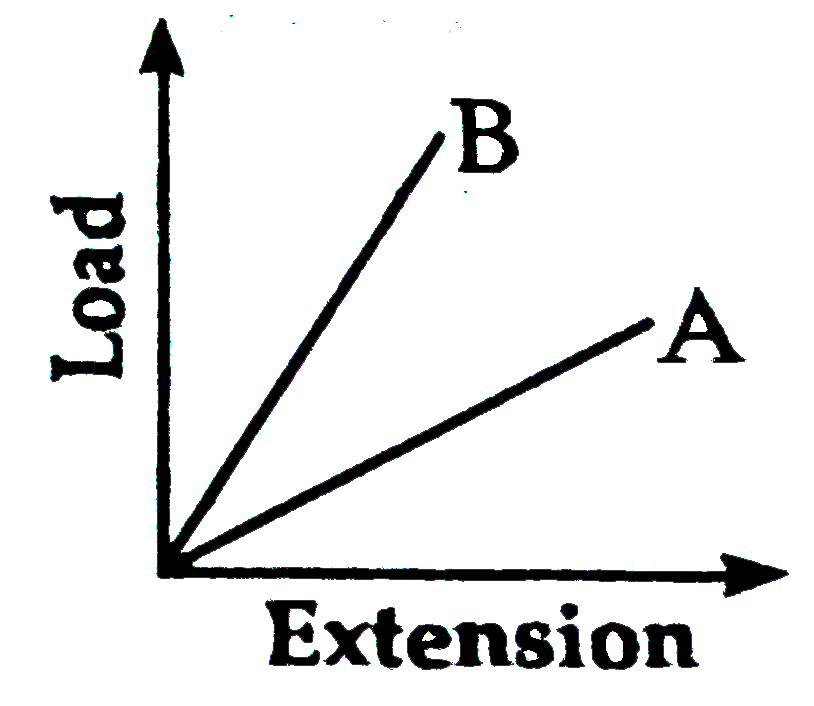
In the given Fig. 7(CF).2, if the dimensions of the two wires are the same and materials are different, Young's modulus is
A
more for A than B
B
more for B than A
C
equal for A and B
D
none of the above
Video Solution
Text Solution
The correct Answer is:A
As, , therefore the graph of F versis is a straight line with slope ,i.e.,
Slope of graph Young's modulus(Y)
As,
|
Topper's Solved these Questions
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Integer Type Questions
12 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Asseration - Reason Type Question
18 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions-II
14 Videos
- PHYSICAL WORLD AND MEASUREMENTBOOK - PRADEEPCHAPTER - PHYSICAL WORLD AND MEASUREMENTEXERCISE - Competiton Focus Jee Medical Entrance
18 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Problem For Practice(a)
25 Videos
Similar Questions
Knowledge Check
When temperature of a material increases, its Young's modulus
AincreasesBdecreasesCremains sameDbecomes infinityThe elastic enery stored in a wire of Young's modulus Y is
AY×Strain2VolumeBStress × Strain × VolumeCStress2×Volume2YD12Y× stress × Strain × VolumeIn an experiment to determine the Young's modulus of the material of a wire, the length of the wire and the suspended mass are doubled. Then the Young's modulus of the wire
Abecomes double'sBbecomes four timeCremains unchangedDbecomes half
Figure shows the strain - stress curve for a given material. The Young's modulus of the material is
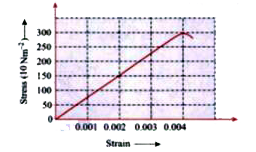
View SolutionIf the density of the material increase, the value of young's modulus
View SolutionIf the length of a wire is doubled, then its Young's modulus
View SolutionTwo wires of the same length l and radius are joined end to end and loaded. If the Young's moduli of the materials of the wires are Y1 and Y2, the combination behaves as a single wire of Young's modulus will be
View Solution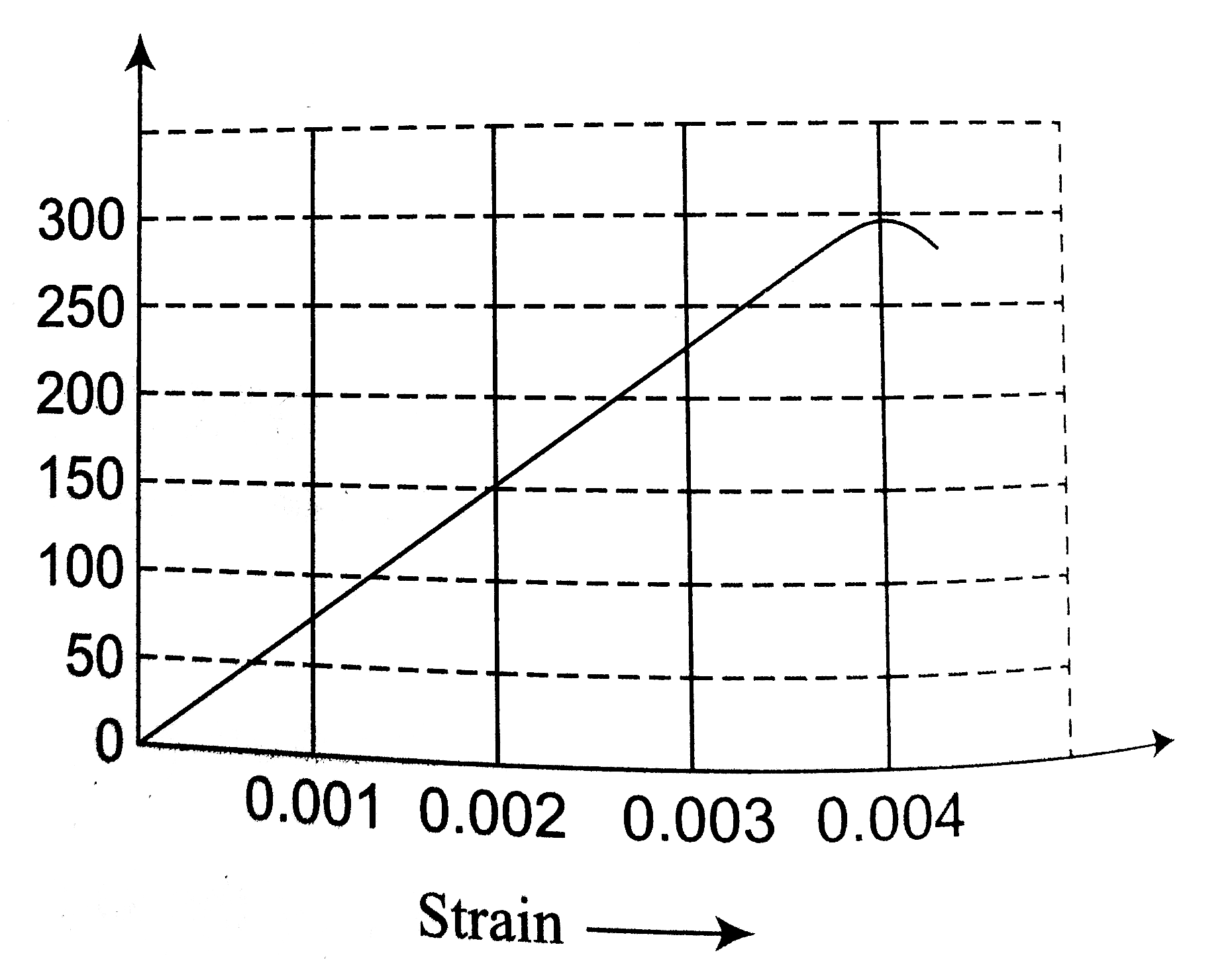
Figure shows the strain stress curve for a given material. The Young's modulus of the material is
View Solution