In the given table, Young's modulus, bulk modulus, and shear modulus of some materials are listed in Columns I, II and III, respectively.

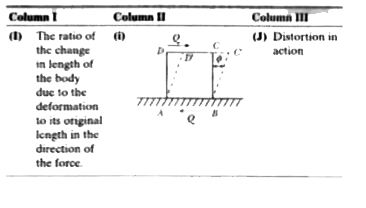
The correct combination that defines the characteristics of lateral strain is

A

(III) (ii) (L)

B

(III) (iv) (M)

C

(II) (iii) (K)

D

(I) (i) (M)

Text Solution

Verified by Experts

(1) $\to$ (d), (2) $\to$ (b), (3) $\to$ (a)

|

Updated on:21/07/2023

Class 12 PHYSICS ELASTICITY

Topper's Solved these Questions

BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Integer Type)
3videos
ELASTICITY
BOOK - RESNICK AND HALLIDAYCHAPTER - ELASTICITYEXERCISE - PRACTICE QUESTIONS (Linked Comprehension)
6videos
ELASTICITY
BOOK - RESNICK AND HALLIDAYCHAPTER - CURRENT AND RESISTANCEEXERCISE - Practice Questions (Integer Type)
3videos
CURRENT AND RESISTANCE
BOOK - RESNICK AND HALLIDAYCHAPTER - ELECTRIC CHARGES AND FIELDSEXERCISE - Practice Questions (Integer Type )
3videos
ELECTRIC CHARGES AND FIELDS

Similar Questions

Knowledge Check

Question 1 - Select One
Find the relation below young's modulus (Y), bulk modulus (K) and shear modulus (G)?
A $Y = 6 K \frac{G}{G + 3 K}$
B $Y = 4 K \frac{G}{G + 3 K}$
C $Y = 9 K \frac{G}{G + 3 K}$
D $Y = 12 K \frac{G}{G + 3 K}$
Question 2 - Select One
Find the relation below young's modulus (Y), bulk modulus (K) and shear modulus (G)?
A $Y = 6 K \frac{G}{G + 3 K}$
B $Y = 4 K \frac{G}{G + 3 K}$
C $Y = 9 K \frac{G}{G + 3 K}$
D $Y = 12 K \frac{G}{G + 3 K}$
Question 3 - Select One
The relation between Y (Young's modulus), K (bulk modulus) and $η$ (shear modulus) is
A $\frac{9}{Y} = \frac{1}{B} + \frac{3}{η}$
B $\frac{1}{Y} = \frac{1}{3 η} + \frac{1}{9 B}$
C $\frac{9}{Y} = \frac{1}{η} + \frac{3}{B}$
D $\frac{1}{η} = \frac{1}{B} + \frac{1}{Y}$

RESNICK AND HALLIDAY-ELASTICITY-PRACTICE QUESTIONS (Matrix - Match)

Home
Ask Doubt
Profile