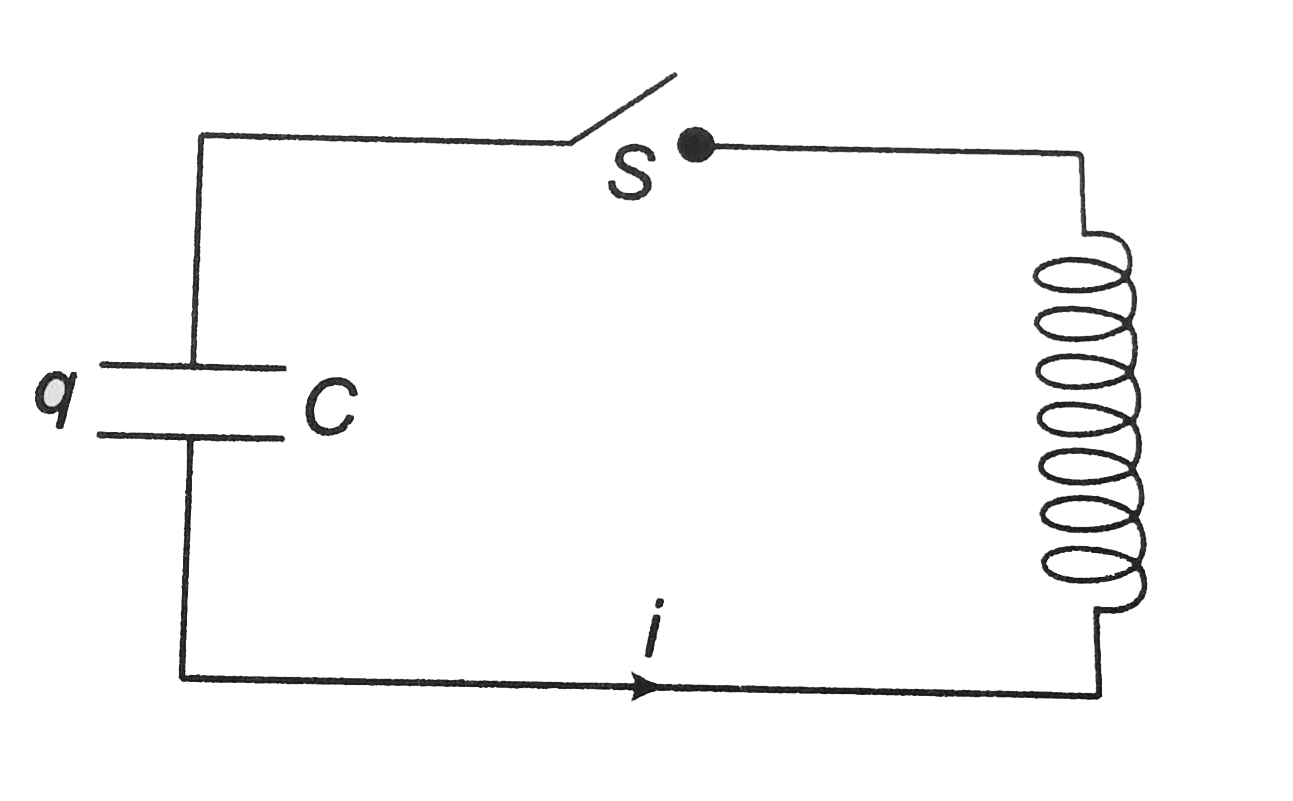
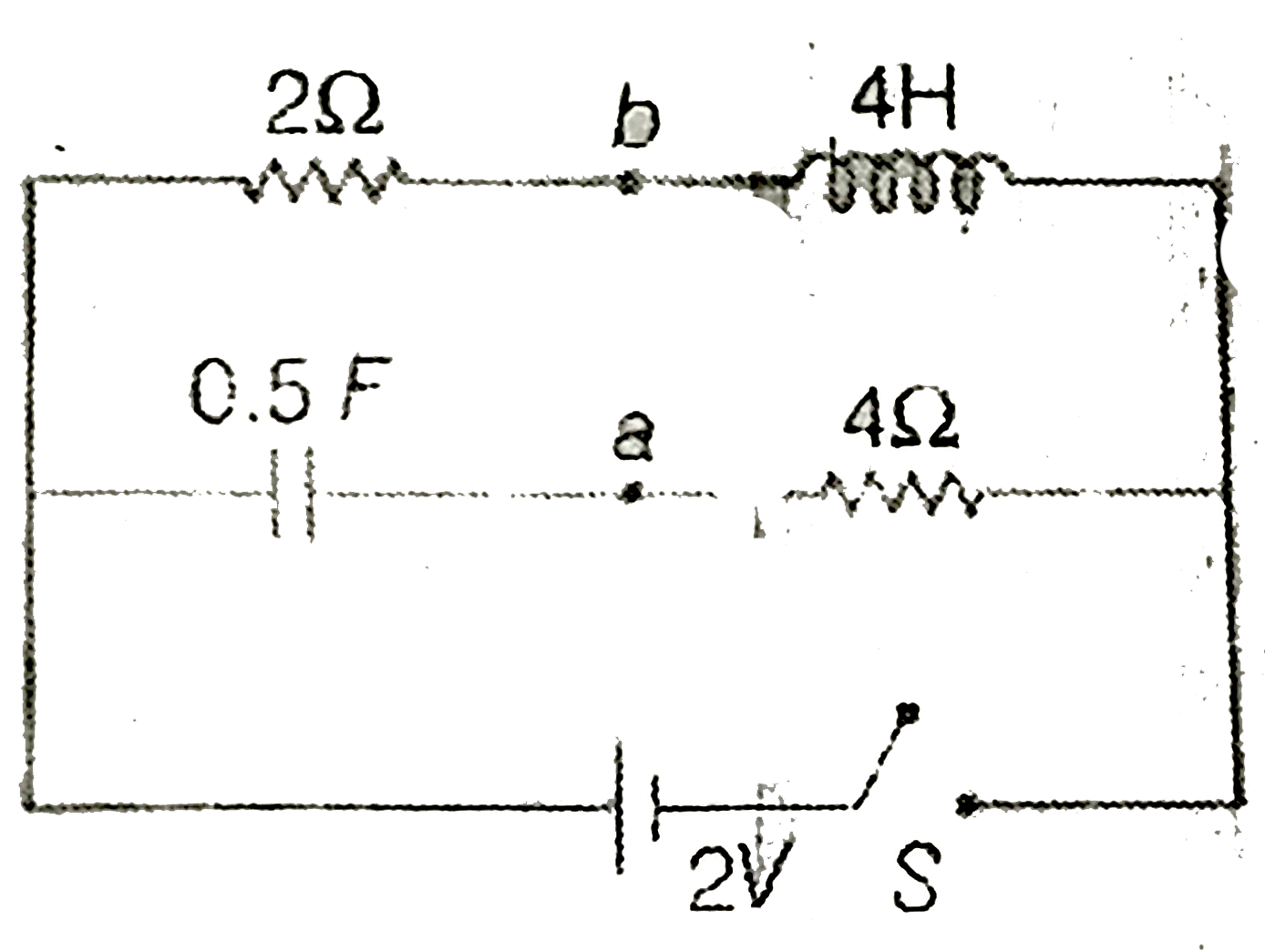In the L−C circuit shown, C=1μF. With capacitor charged to 100V, switch S is suddenly closed at time t=0. The circuit then oscillates at 103Hz
(a) Calculate co and T
(b) Express q as a function of time
(c) Calculate L
(d) Calculate the average current during the first quarter-cycle.
The correct Answer is:A, D
a.ω=2πf,T1f
b. At t=0,q=q0=CV0=(100μC)
Now, q=q0cosωt
c. ω=1√LC⇒L=1ω2C
d. |i|=∣∣∣dqdt∣∣∣=q0ωsinωt
Average value of current in first quarter cycle
=∫T/40dtT/4
Topper's Solved these Questions
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 Single Correct37videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Level 2 More Than One Correct10videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Objective Questions3videos
ELECTROMAGNETIC INDUCTION
- BOOK - DC PANDEYCHAPTER - CURRENT ELECTRICITYEXERCISE - Medical entrances gallery97videos
CURRENT ELECTRICITY
- BOOK - DC PANDEYCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - Sec C22videos
ELECTROMAGNETIC WAVES
Similar Questions
Knowledge Check
- Question 1 - Select One
In the circuit shown, the capacitor C1 is initially charged with charge q0. The switch S is closed at time t = 0 . The charge on C2 after time t is
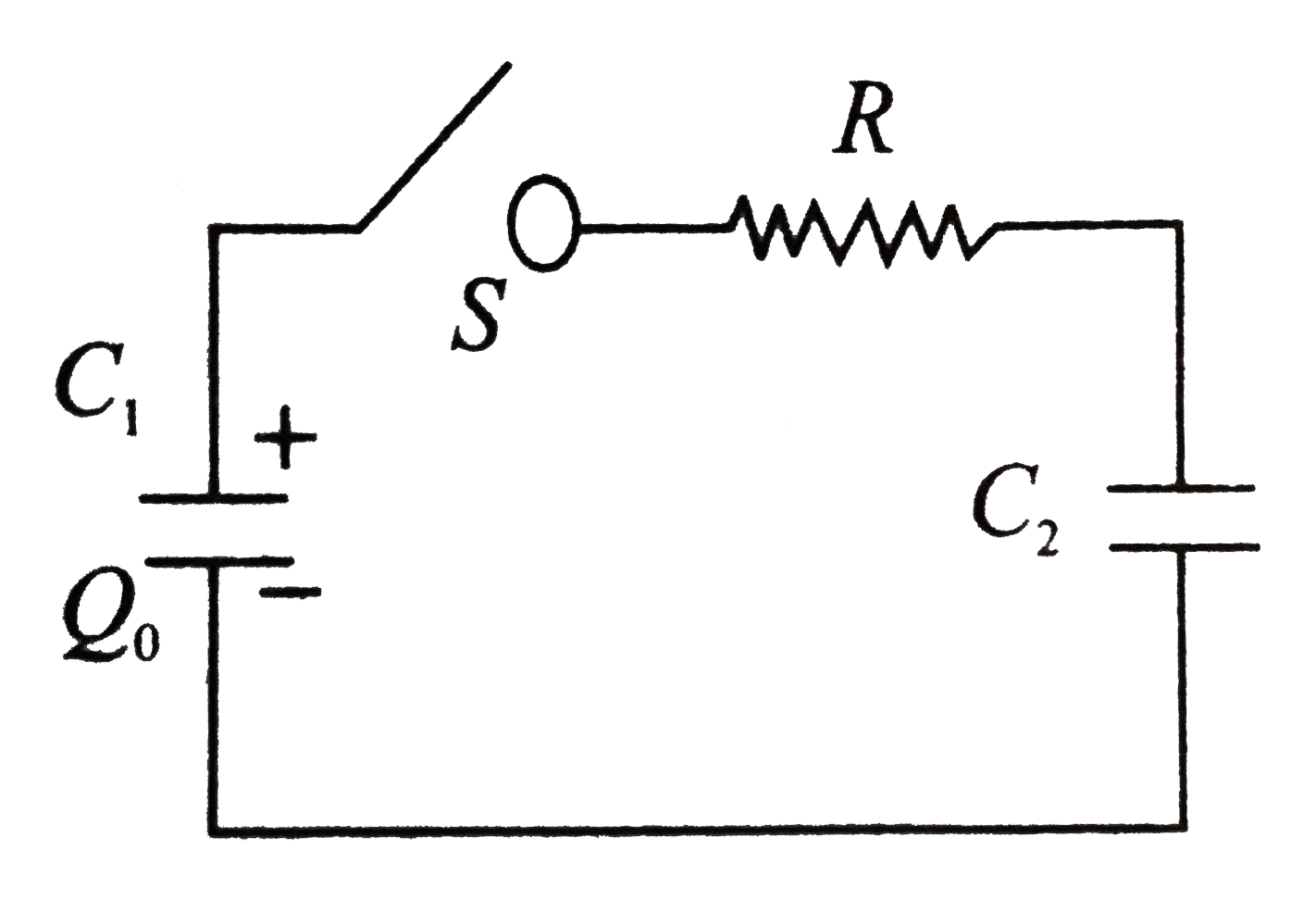 Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R)
Aq0C1C1+C2(1−e−t(C1+C2)C1C2R)Bq0C2C1+C2(1−e−t(C1+C2)C1C2R)Cq0C1C1+C2(1−e−tC2R)Dq0C2C1+C2(1−e−tC2R) - Question 2 - Select One
In the circuit shown in figure, the capacitor is charged with a cell of 5V.If the switch is closed at t=0, then at t=12s, charge on the capacitor is
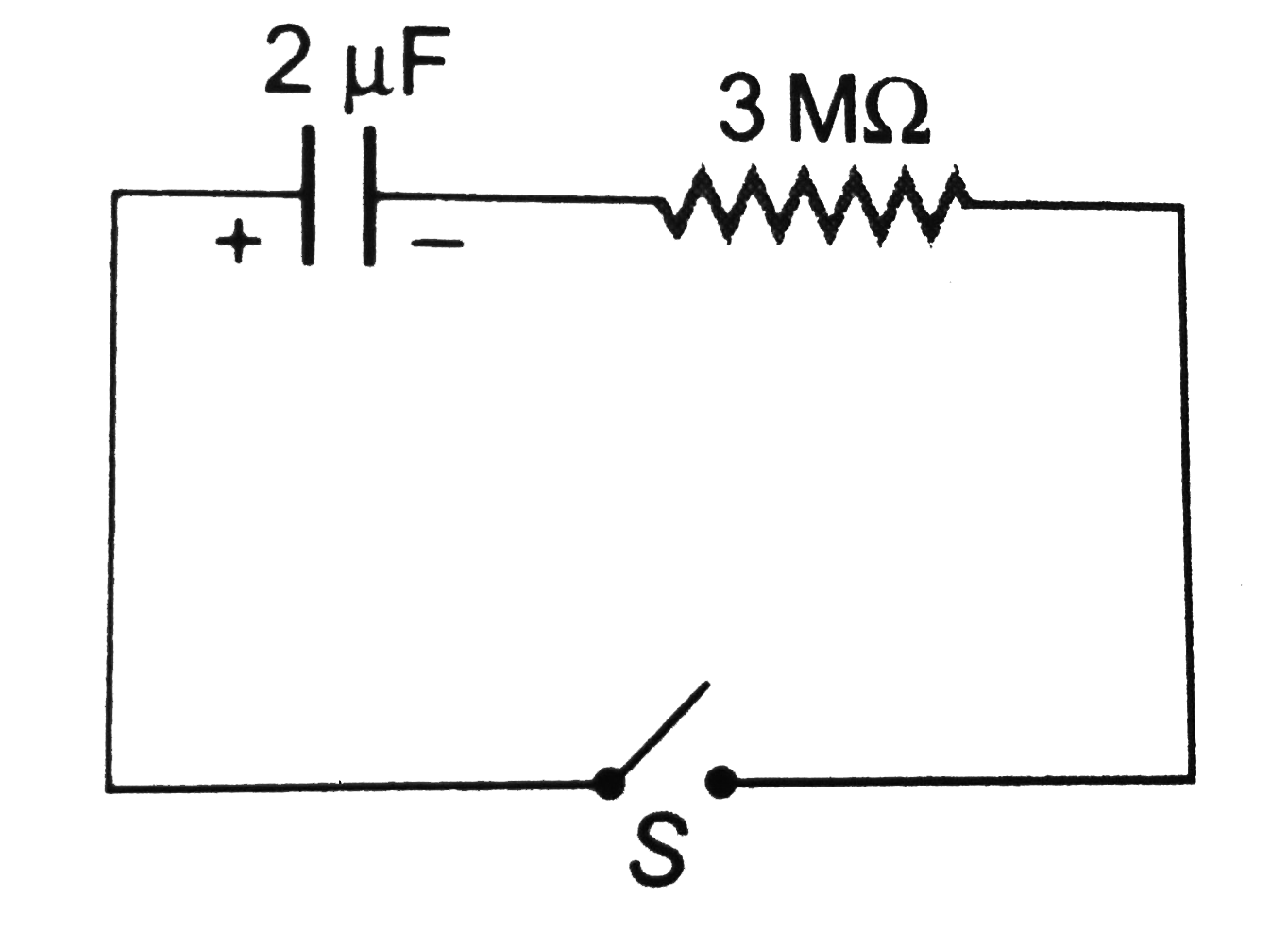 A(0.37)10μCB(0.37)210μCC(0.63)10μCD(0.63)210μC
A(0.37)10μCB(0.37)210μCC(0.63)10μCD(0.63)210μC - Question 3 - Select One
In the circuit shown if Fig. the switch S is closed at time t = 0. The current through the capacitor and inductor will be equal at time t equal (given R=√L/C
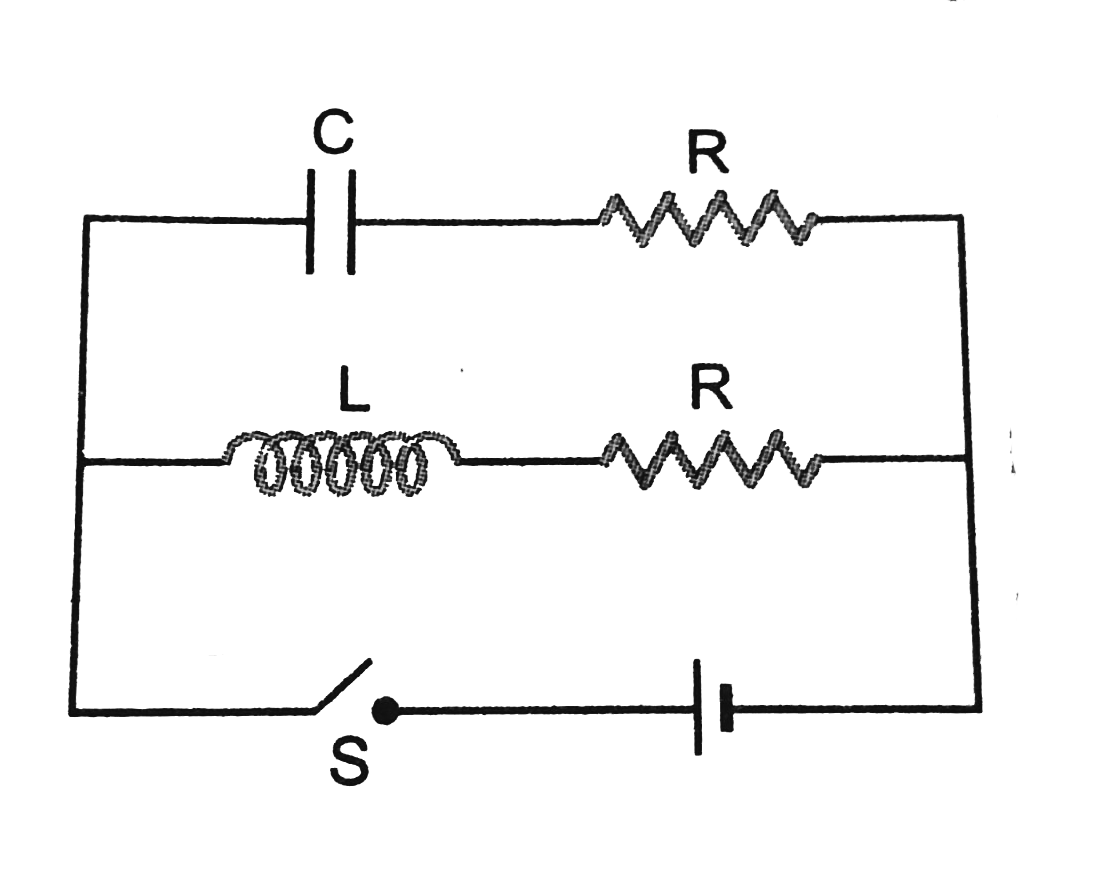 ARCBRCloge2C1RlogeDLR
ARCBRCloge2C1RlogeDLR
In the circuit shown in figure-5.115, find the current in inductor as a function of time if switch is closed at t=0.
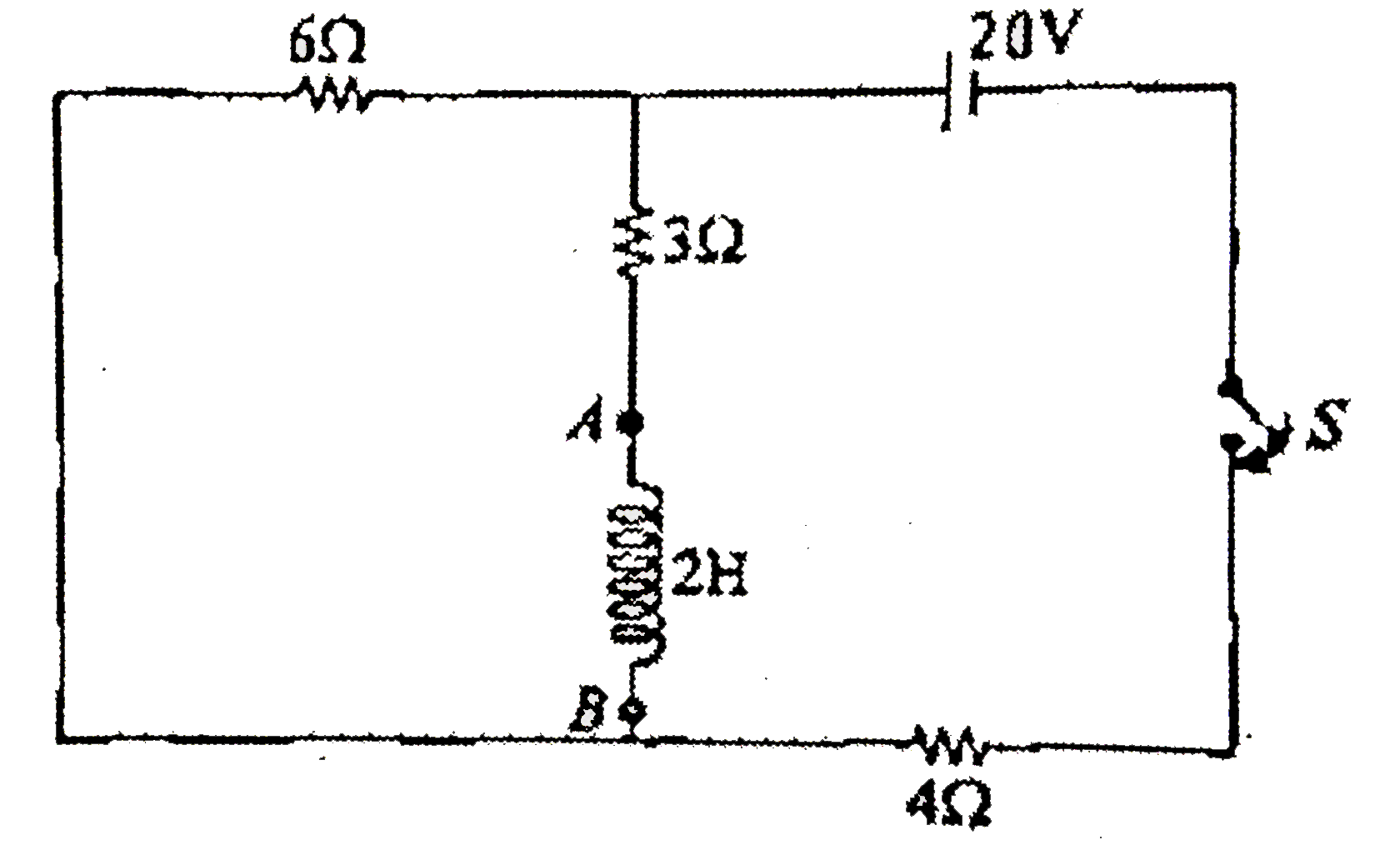 View Solution
View SolutionIn the circuit shown in the figure, switch S is closed at time t=0. Charge on positive plate of capacitor is q at time t.
(a) Derive a differential equation for q at time t.
(b) Solve the equation to write q as a function of time.
(c) Put t = 0 and t=∞ in your equation to get charge on the capacitor at these times.
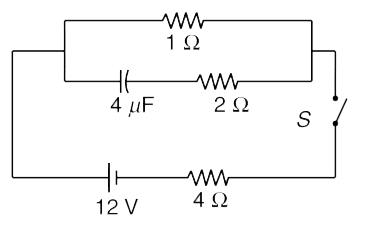 View Solution
View SolutionIn the circuit shown in fig, if the switch S is closed at t=0 , the capacitor charges with a time constant
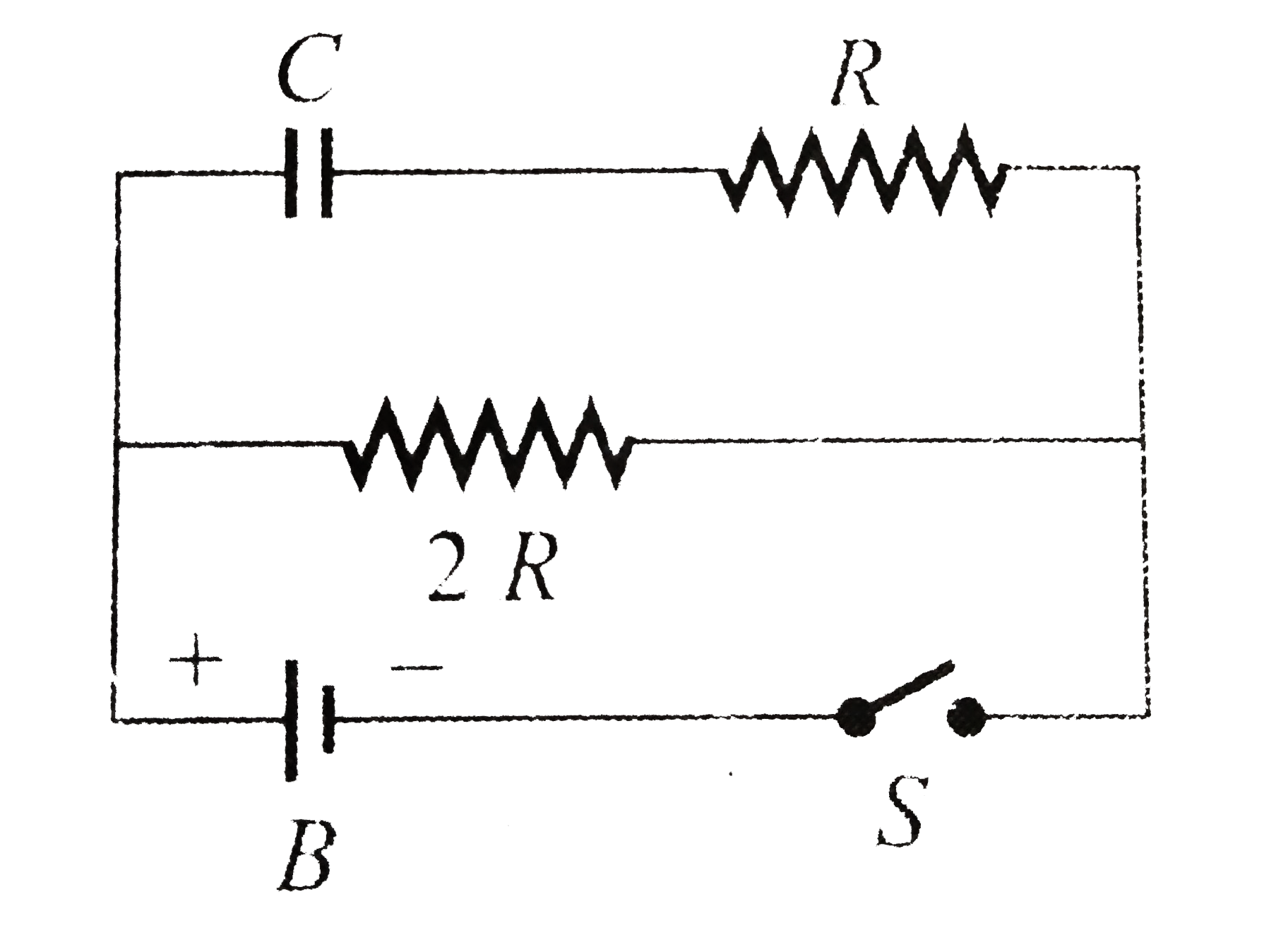 View Solution
View SolutionThe switch S in the circuit diagram is closed at t = 0. The charge on capacitors at any time is
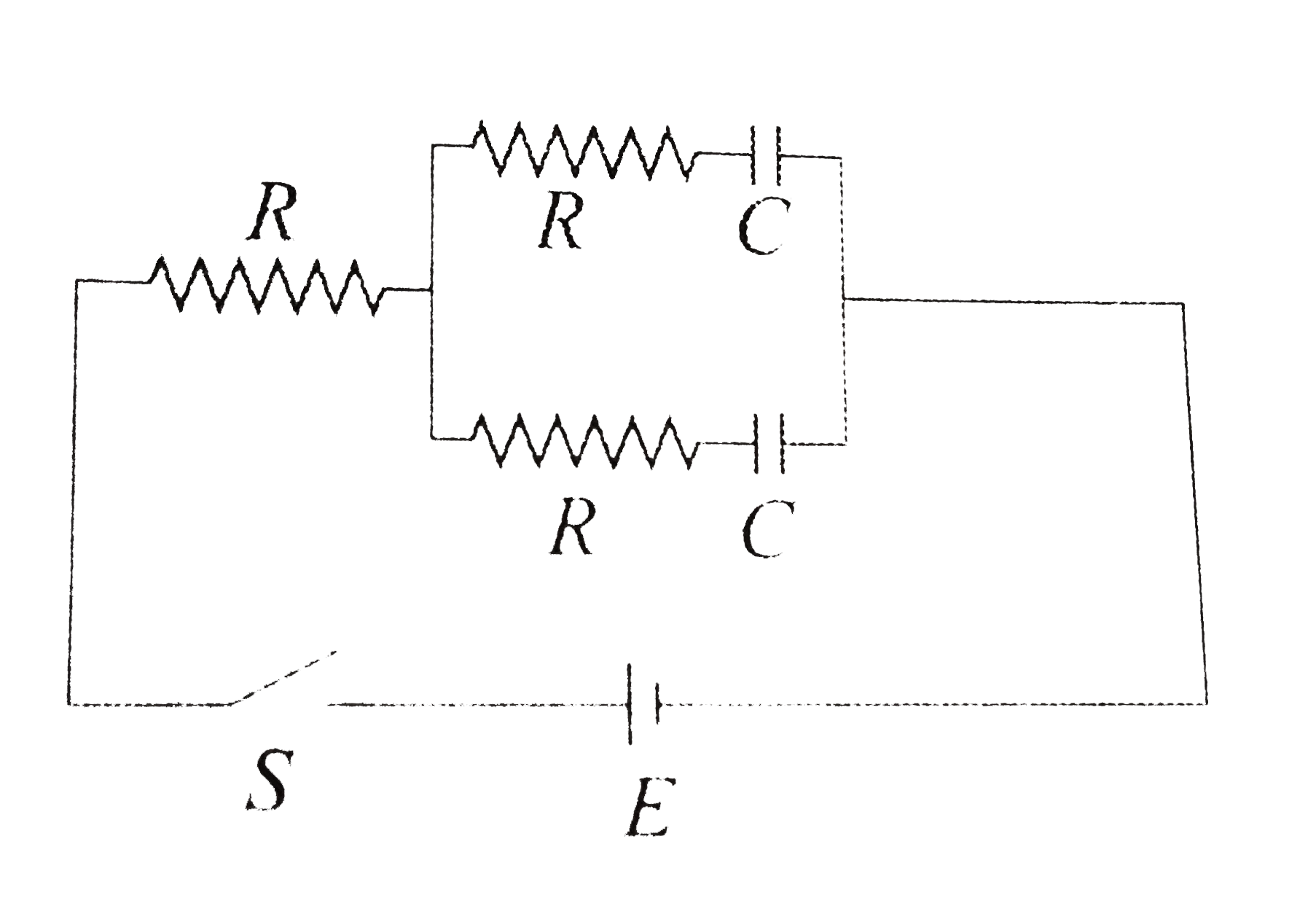 View Solution
View Solutionn the circuit shown in the figure, the capacitor C is charged to a potential Vo The heat generated and charge flow, in the circuit to when the switch S is closed, is
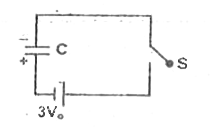 View Solution
View Solution