In the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: is the linear momentum, is the angular momentum about the origin, is the kinetic energy, is the potential energy and is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path.
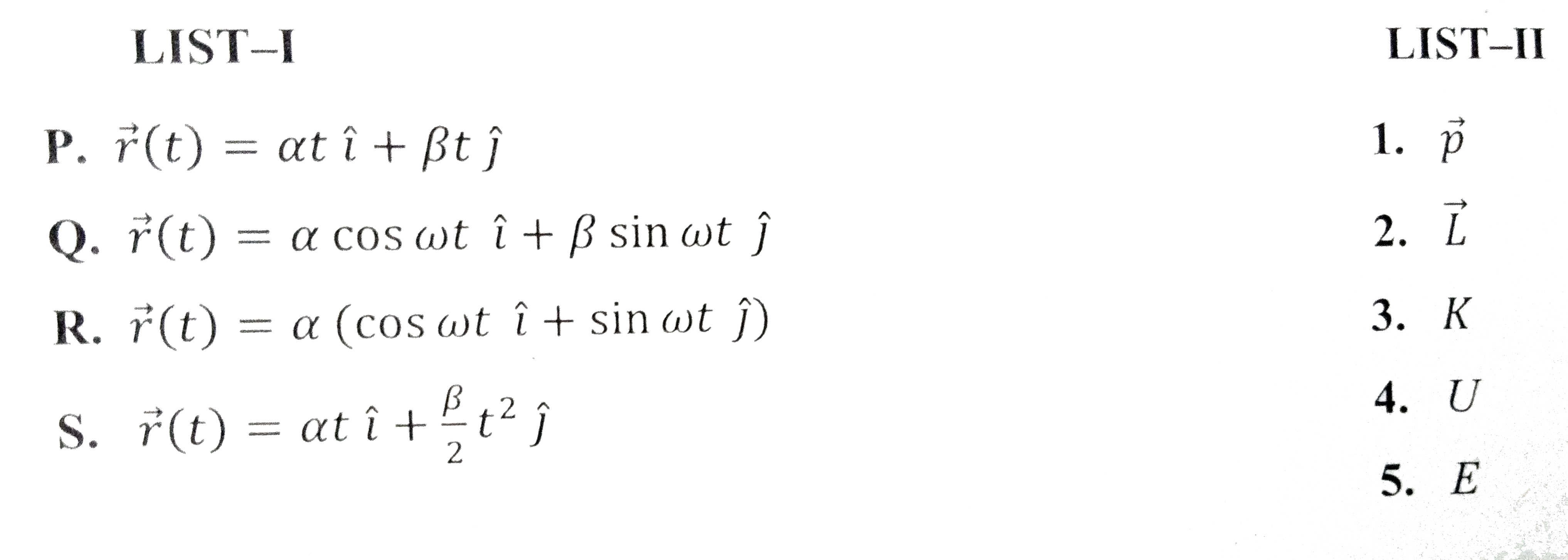
In the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: is the linear momentum, is the angular momentum about the origin, is the kinetic energy, is the potential energy and is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path.

A

p-1,2,3,4,5, Q-2,5, R-2,3,4,5,S-5

B

p-1,2,3,4,5, Q-3,5, R-2,3,4,5,S-2,5

C

p-2,3,4,5, Q-,5, R-1,S-2,5

D

p-1,2,3,5, Q-2,5, R-2,3,4,5,S-2,5

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for In the List-I below, four different paths of a particle are given as functions of time. In these functions, and are positive constants of appropriate dimensions and . In each case, the force acting on the particle is either zero or conservative. In List-II, five physical quantities of the particle are mentioned: is the linear momentum, is the angular momentum about the origin, is the kinetic energy, is the potential energy and is the total energy. Match each path in List-I with those quantities in List-II, which are conserved for that path. by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.

Updated on:21/07/2023
Class 11PHYSICSSYSTEM OF PARTICLES AND ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • The angular momentum of a particle is

    Aparallel to its linear momentum
    Bperpendicular to its linear momentum
    Cinclined to its linear momentum
    Da scalar quantity

  • The linear momentum p of a particle is given as a function of time t as p=At2+Bt+C.The dimensions of constant B are

    A[ML−1T−1]
    B[ML−1T−2]
    C[MLT−2]
    D[MLT−1]

  • A particle has a linear momentum p and position vector r. the angular momentum of this particle about the origin will not be zero under the conditions

    Ap=0
    Bp is perpendicular to r and does not cross r
    Cp is anti-parallel to r
    Dthe particle passes through the origin.