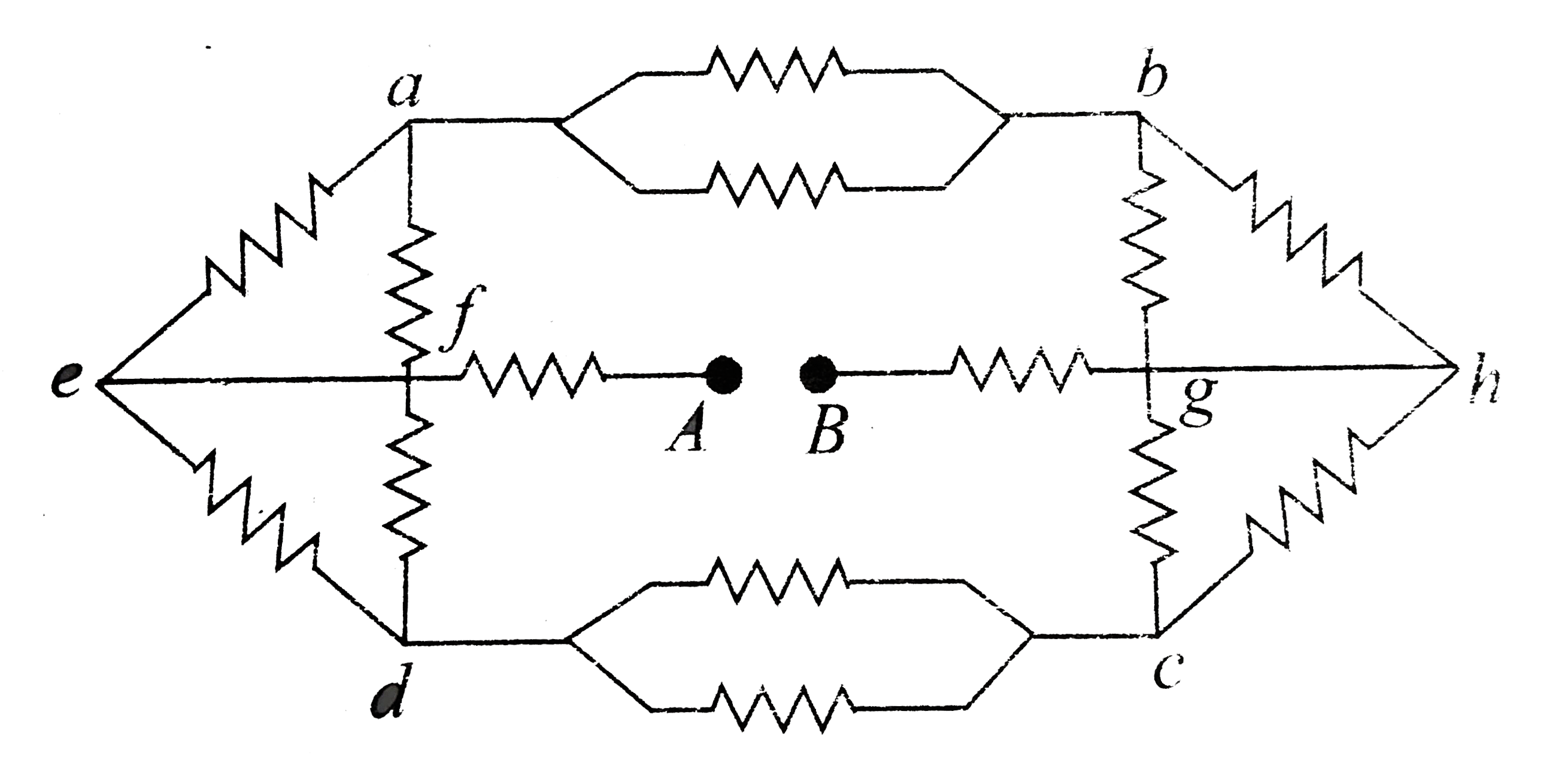
In the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and B is
3R4
5R6
7R12
4R3
The correct Answer is:C
If we connect a battery across A and
B, then E and D will be at the same
potential and F and C will be at the
same potential.

Req(AB)=7R12
If we connect the battery across A
and G, the B, E, and D will be at
the same potential. C,F, and H will
be at the same potential.
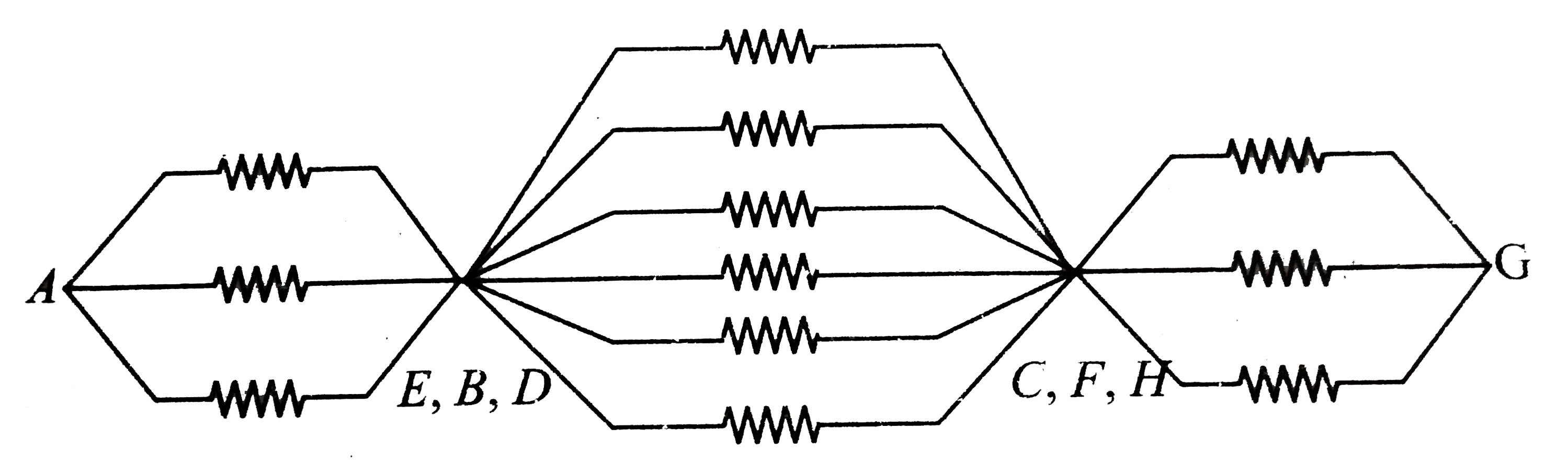
If we connect the battery across A and C, then no current will flow in
the resistances between B and F and between H and D. So they can
be removed. Thus,
Req=3R4
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Interger8videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT AND CIRCUITEXERCISE - Multiple Correct16videos
ELECTRIC CURRENT AND CIRCUIT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits15videos
ELECTRIC CURRENT & CIRCUITS
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC FLUX AND GAUSS LAWEXERCISE - MCQ s38videos
ELECTRIC FLUX AND GAUSS LAW
Similar Questions
In the netwrok shown in fig. each resistance is R.

The equivalent resistance between A and G isView SolutionIn the network shown in fig. each resistance is R.

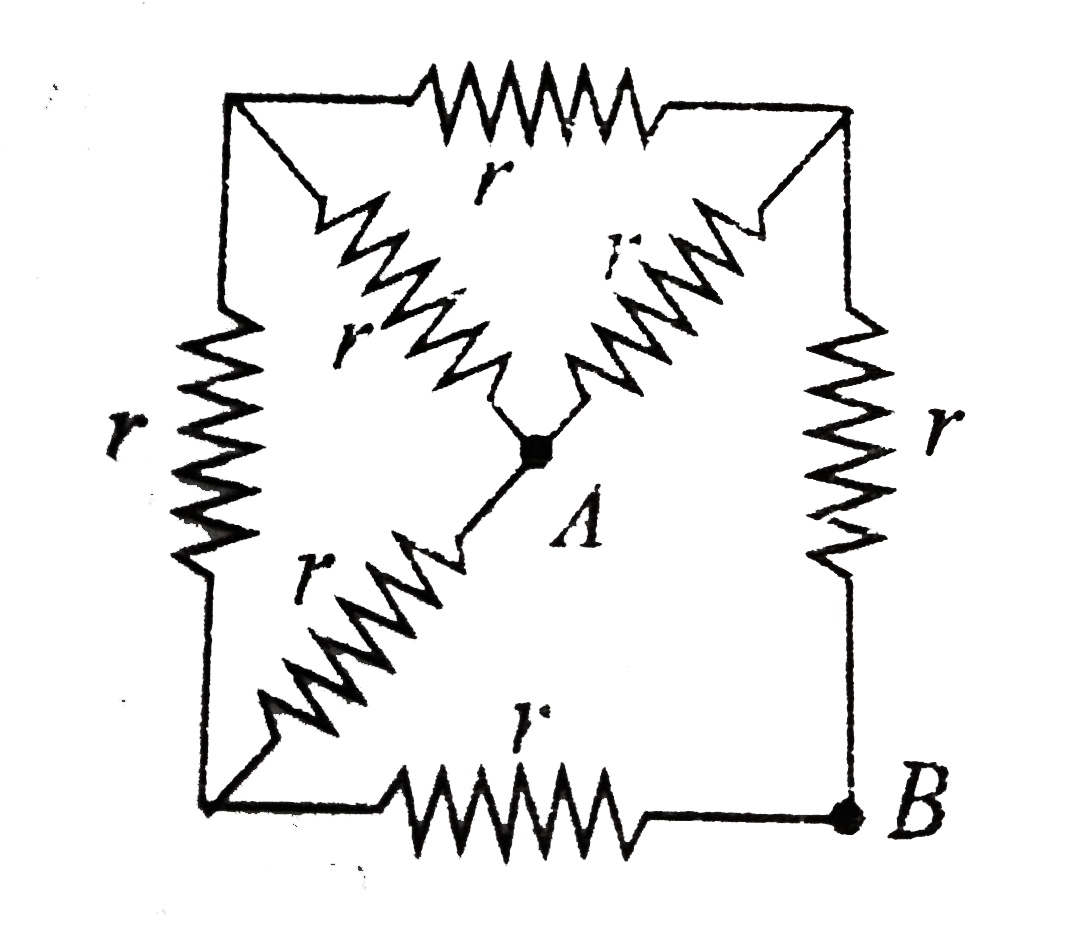
The equivalent resistance between A and C isView SolutionEquivalent resistance between A and B in Fig. is
 View Solution
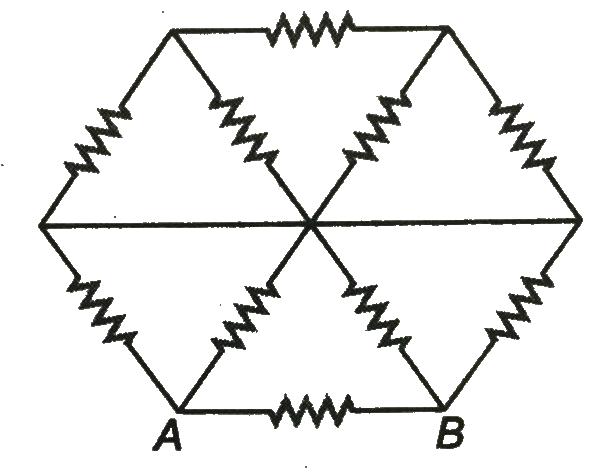
View SolutionIn the network shown in figure, each resistance is R. The equvalent resistance between points A and B is
 View Solution
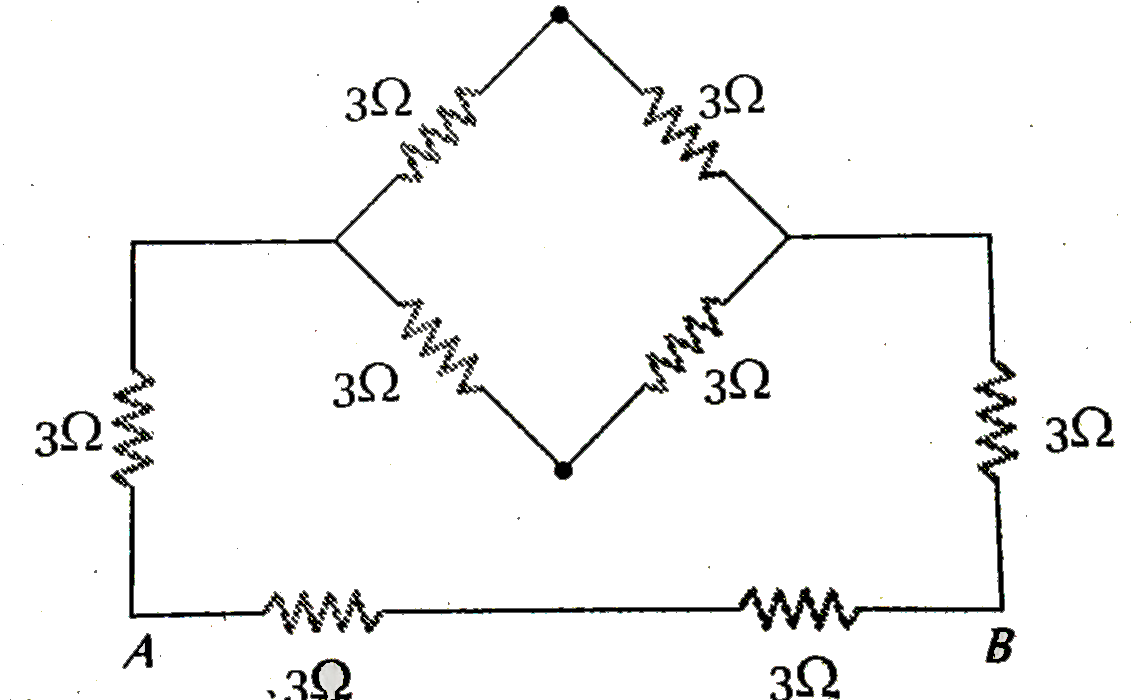
View SolutionEquivalent resistance between A and B will be
 View Solution
View SolutionIn the network shown, each resistance is R. Calculate the equivalent resistance between A and B.
 View Solution
View SolutionEach of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
 View Solution
View SolutionIn the arrangement shown, the magnitude of each resistance is 1Ω. The equivalent resistance between O and A is given by
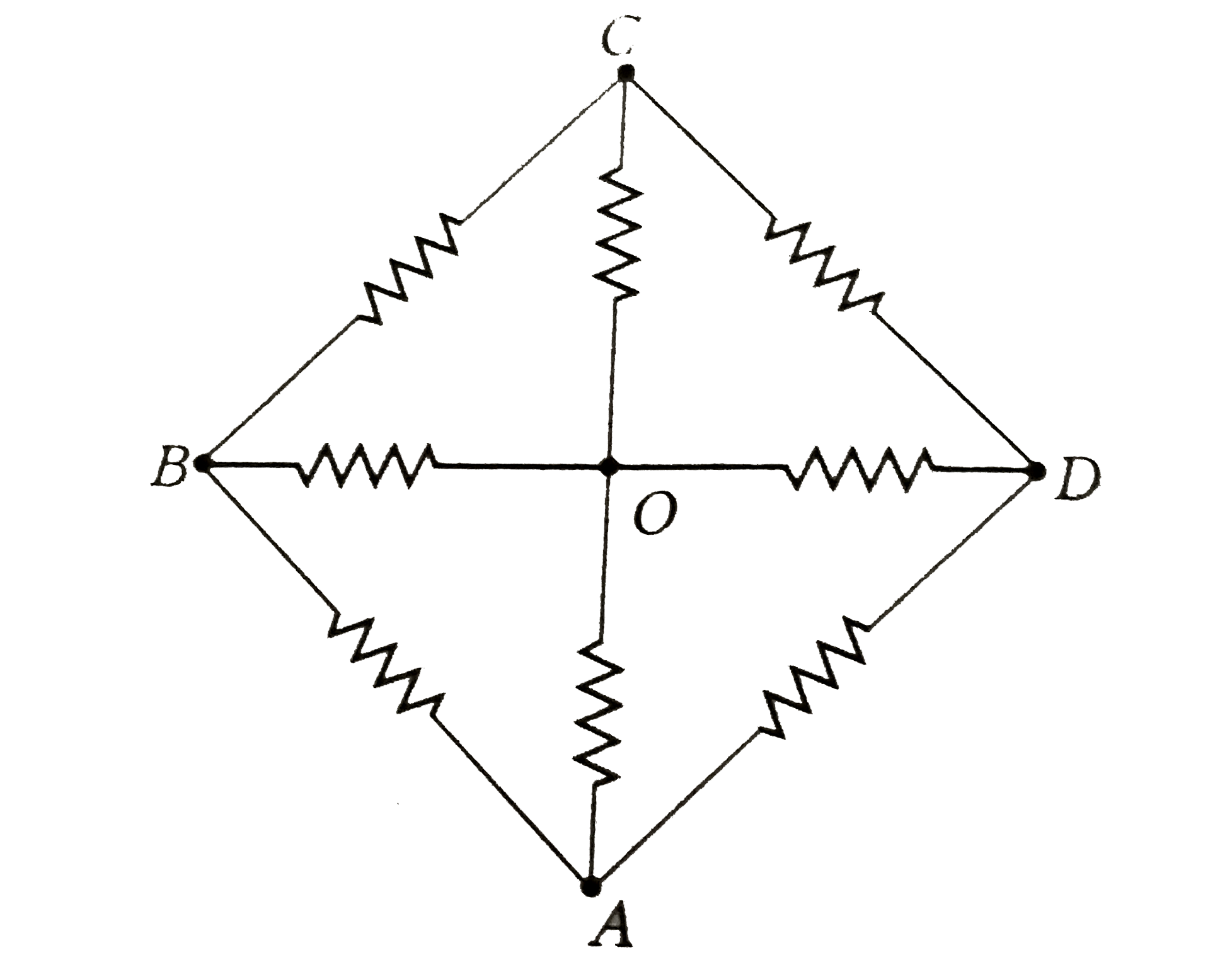 View Solution
View SolutionIn the network shown, the equivalent resistance between A and B is
 View Solution
View SolutionIn the network shown in Fig., calculate the equivalent resistance between the points
A and B,
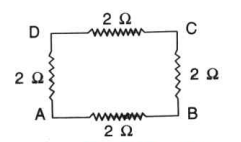 View Solution
View Solution

