In the question number 93, the time elapsed for its mechanical energy to drop half of its initial value is
2.5 s
3.5 s
4.5 s
7.5 s
The correct Answer is:B
The energy of the damped oscillator at any instant t is given by
E=E0e−bt/m
Where E0 is its initial enegy and b is the damping constant.
At t=t1/2, the energy drop to half of its initial value.
From eq. (i), we get
E02=E0e−bt1/2m 12=e−bt1/2/m
Taking natural logarithm on both sides, we get
ln(12)=−bt1/2m,t1/2=−mln(1/2)b . . . (ii)
here, ln(1/2)=−0.693
b=40gs−1,m=200g
substituting in eq. (ii) , we get
t1/2=0.693×200g40gs−1=3.5s
Topper's Solved these Questions
- BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Forced Oscillation And Resonance6videos
OSCILLATIONS
- BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Higher Order Thinking Skills8videos
OSCILLATIONS
- BOOK - NCERT FINGERTIPSCHAPTER - OSCILLATIONS EXERCISE - Some Systems Executing Simple Harmonic Motion29videos
OSCILLATIONS
- BOOK - NCERT FINGERTIPSCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - Assertion And Reason15videos
MOTION IN A STRAIGHT LINE
- BOOK - NCERT FINGERTIPSCHAPTER - PHYSICAL WORLDEXERCISE - Assertion And Reason10videos
PHYSICAL WORLD
Similar Questions
In damped oscillatory motion a block of mass 20kg is suspended to a spring of force constant 90N/m in a medium and damping constant is 40g/s. Find (a) time period of oscillation (b) time taken for amplitude of oscillation to drop to half of its intial value (c) time taken for its mechanical energy to drop to half of its initial value.
View SolutionFor the damped oscillator shown in Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.View Solution
Knowledge Check
- Question 1 - Select One
A block of mass 0.1 kg is connected to an elastic spring of spring constant 640 Nm−1 and oscillates in a medium of constant 10−2 kg s−1. The system dissipates its energy gradually. The time taken for its mechanical energy of vibration to drop to half of its initial value, is closest to :
A2 sB3.5 sC5 sD7 s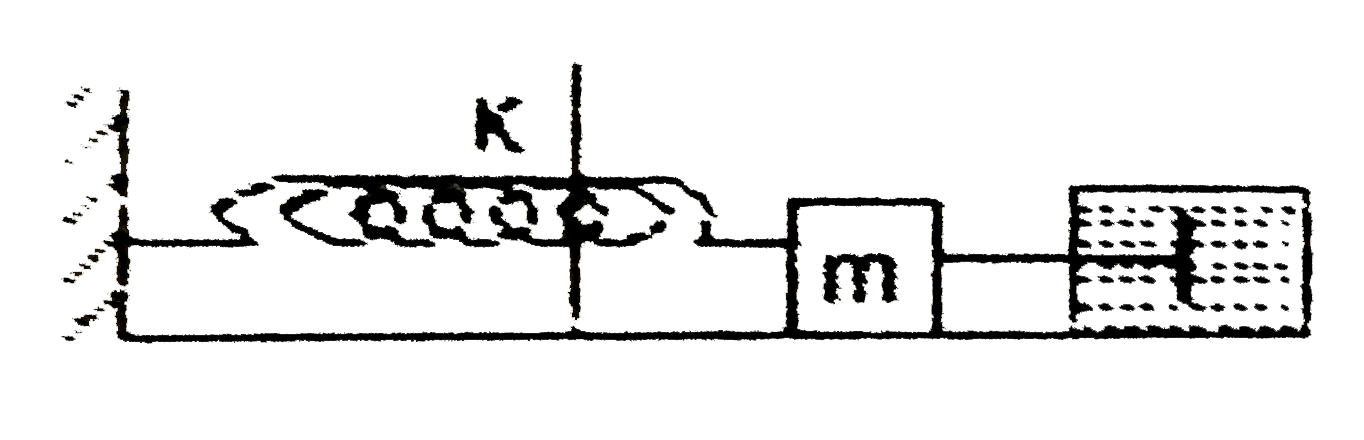 - Question 2 - Select One
For a damped oscillator which follow the equation →F=−k→x−b→V
the mass of the block is 100 gm K=100N/M and the damping constant is 20 gm/sec. thhen find the time taken for its mechanical energy to drop to one-fourth of its initial value.A1.73B3.46C6.93D13.84 - Question 3 - Select One
A block of mass 200 g executing SHM under the influence of a spring of spring constant k=90Nm−1 and a damping constant b=40gs−1. The time elapsed for its amplitude to drop to half of its initial value is (Given, ln (1/2)=−0.693)
A7sB9sC4sD11s
For the damped oscillator shown in previous Figure, the mass m of the block is 400 g, k=45Nm−1 and the damping constant b is 80gs−1. Calculate .
(a) The period of osciallation ,
(b) Time taken for its amplitude of vibrations to drop to half of its initial value and
(c ) The time taken for its mechanical energy to drop to half its initial value.View Solution-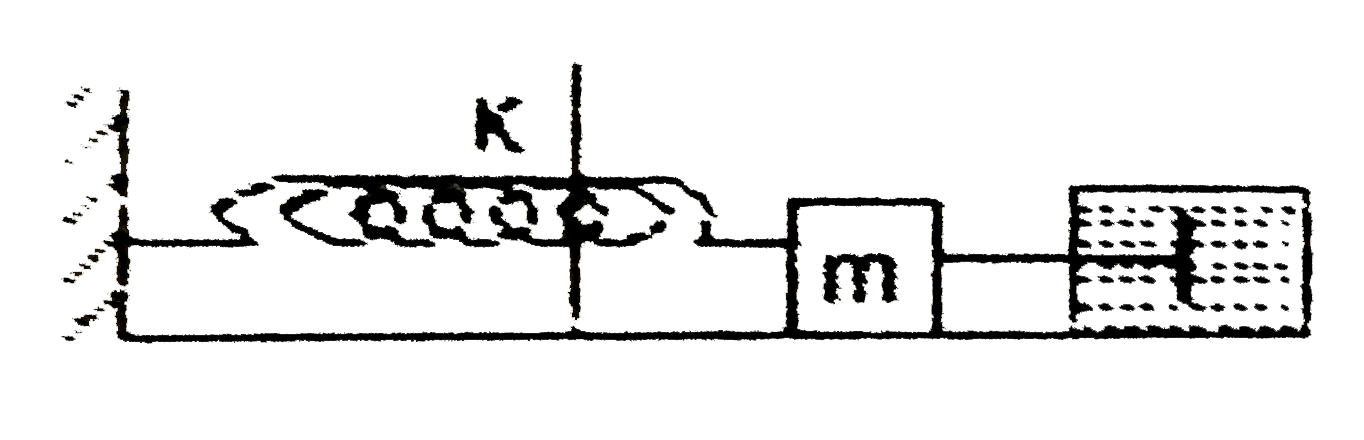
For a damped oscillator which follow the equation →F=−k→x−b→V
the mass of the block is 100 gm K=100N/M and the damping constant is 20 gm/sec. thhen find the time taken for its mechanical energy to drop to one-fourth of its initial value.View Solution For the damped oscillator shown in Fig, the mass of the block is 200g,k=80Nm−1 and the damping constant b is 40gs−1 Calculate
(a) The period of oscillation
(b) Time taken for its amplitude of vibrations to drop to half of its initial values
(c) The time for the mechanical energy to drop to half initial values
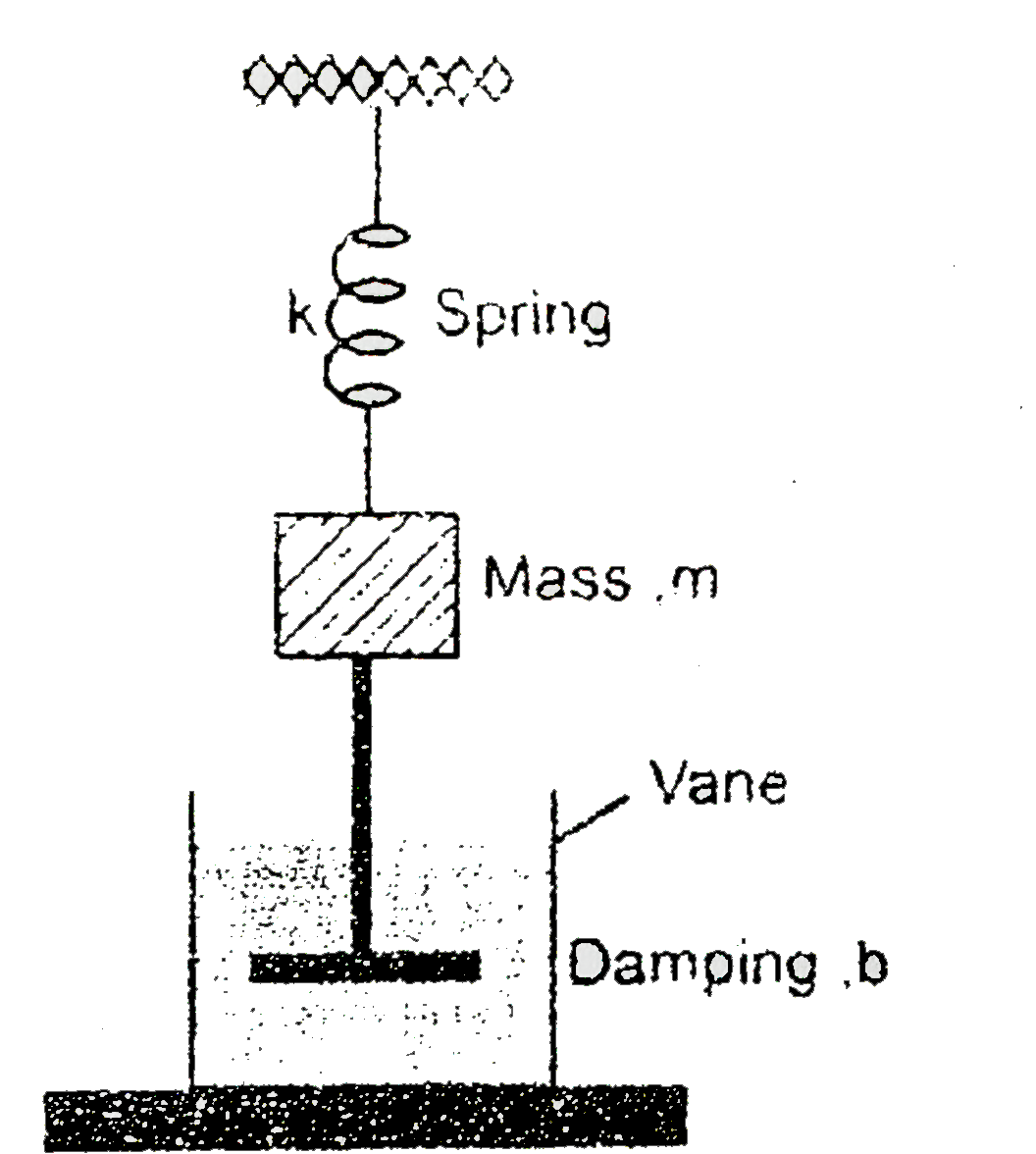
View SolutionFor the damped oscillator of Fig. 15.20, m= 250g, k= 85N/m, and b= 70g/s
How long does it take for the mechanical energy to drop to one-half its initial value?View SolutionAmplitude of mass spring system which is executing SHM decreases with time. If mass = 500g decay constant = 20 g/s then how much time is required for the amplitude of the system to drop to half of its initial value.
View Solution