Lateral displacement of ray passing through a glass slab
A ray of light is incident on a parallel sided glass slab of refractive index n and thickness t as shown in Fig. 34-2. Find the lateral displacement of the ray as it passes through the slab.
To find the lateral displacement of a ray passing through a parallel-sided glass slab, we can follow these steps:
1. Understanding the Setup:
- We have a glass slab with thickness t and refractive index n.
- A ray of light is incident on one face of the slab at an angle of incidence i and refracts into the slab at an angle r.
2. Refraction at the First Surface:
- When the ray enters the glass slab, it bends towards the normal due to the higher refractive index of glass compared to air.
- According to Snell's Law:
n1sin(i)=n2sin(r)
where n1 is the refractive index of air (approximately 1) and n2=n for glass.
3. Refraction at the Second Surface:
- As the ray exits the glass slab into air, it bends away from the normal.
- Again applying Snell's Law at the second surface:
nsin(r)=n1sin(i′)
where i′ is the angle of incidence at the second surface, which is equal to r due to the parallel nature of the slab.
4. Lateral Displacement:
- The lateral displacement Δ can be determined by analyzing the geometry of the ray path through the slab.
- We can form two right triangles:
- Triangle formed by the incident ray and the normal at the first surface.
- Triangle formed by the refracted ray and the normal at the second surface.
5. Using Trigonometric Relationships:
- In the triangle formed by the incident ray, we can express the lateral displacement Δ as:
Δ=t⋅sin(i−r)
- The base of the triangle can be expressed using the cosine of the angle r:
Δ=t⋅sin(i−r)cos(r)
6. Final Expression:
- Thus, the final expression for the lateral displacement Δ of the ray as it passes through the slab is:
Δ=t⋅sin(i−r)cos(r)
- We have a glass slab with thickness t and refractive index n.
- A ray of light is incident on one face of the slab at an angle of incidence i and refracts into the slab at an angle r.
- When the ray enters the glass slab, it bends towards the normal due to the higher refractive index of glass compared to air.
- According to Snell's Law:
n1sin(i)=n2sin(r)
where n1 is the refractive index of air (approximately 1) and n2=n for glass.
- As the ray exits the glass slab into air, it bends away from the normal.
- Again applying Snell's Law at the second surface:
nsin(r)=n1sin(i′)
where i′ is the angle of incidence at the second surface, which is equal to r due to the parallel nature of the slab.
- The lateral displacement Δ can be determined by analyzing the geometry of the ray path through the slab.
- We can form two right triangles:
- Triangle formed by the incident ray and the normal at the first surface.
- Triangle formed by the refracted ray and the normal at the second surface.
- In the triangle formed by the incident ray, we can express the lateral displacement Δ as:
Δ=t⋅sin(i−r)
- The base of the triangle can be expressed using the cosine of the angle r:
Δ=t⋅sin(i−r)cos(r)
- Thus, the final expression for the lateral displacement Δ of the ray as it passes through the slab is:
Δ=t⋅sin(i−r)cos(r)
Topper's Solved these Questions
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Check point
6 Videos
- GEOMETRICAL OPTICS : REFRACTIONBOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFRACTIONEXERCISE - Problems
44 Videos
- GEOMETRICAL OPTICS : REFLECTION BOOK - RESNICK AND HALLIDAYCHAPTER - GEOMETRICAL OPTICS : REFLECTION EXERCISE - PRACTICE QUESTIONS (Integer Type)
3 Videos
- GRAVITATIONBOOK - RESNICK AND HALLIDAYCHAPTER - GRAVITATIONEXERCISE - PRACTICE QUESTIONS (INTEGER TYPE)
4 Videos
Similar Questions
Knowledge Check
A ray of light 10−9 second to cross a glass slab of refractive index 1.5. The thickness of the slab will be
A0.1 mB0.2 mC0.3 mD0.4 mA ray of light is incident on a parallel slab of thickness t and refractive index n. If the angle of incidence θ is small, than the lateral displacement in the incident and emergent ray will be
Atθ(n−1)nBtθnCtθnn−1Dtθ(n+1)nA ray of light is incident upon a parallel sided transparent slab of thickness 9 cm at an angle of incidence 60° • If the angle of refraction is 30°, the lateral displacement of the light ray is
A√3cmB3√3cmC3cmD2√3 cm
Lateral displacement depends on ______ of the glass slab.
View SolutionA ray of light suffers lateral displacement on passing through a parallel sided glass slab. What is the maximum possible value of lateral displacement ?
View SolutionMaximum lateral displacement of ray light incident on a slab of thickness t is
View SolutionA ray of light is incident on a parallel-sided glass slab as shown in the figure. The angle of refraction for this ray of light is likely to be :
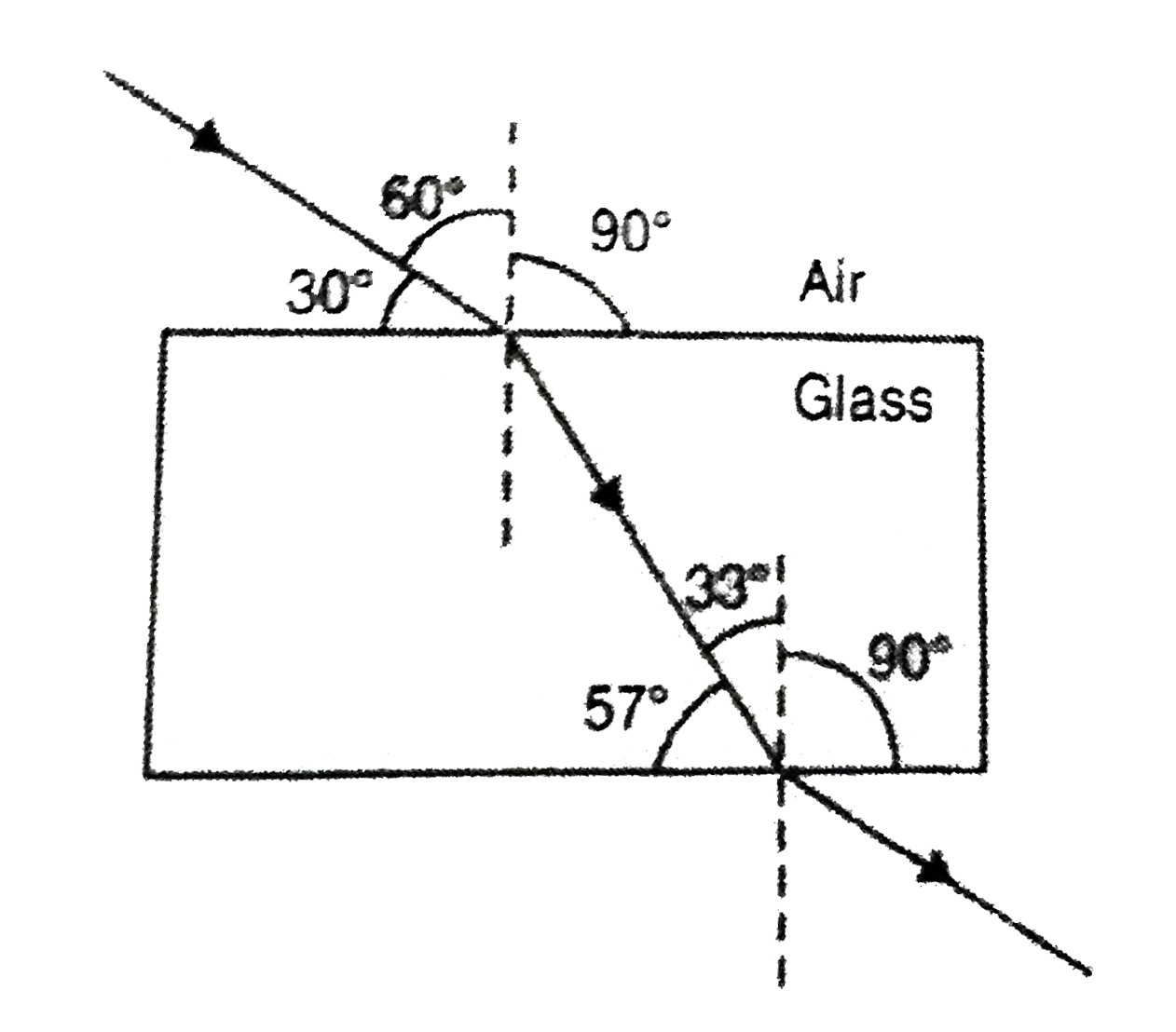
View SolutionA ray of light is incident on a glass slab of refractive index 1.5, making an angle of 40∘ with the surface. The angle of refraction in glass is
View Solution
