Let IA and IB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of mass of the body but B does not
IA<IB
If IA<IB the axes are parallel
If the axes are paralel IA<IB
if the axes are not parallel the IA≥IB
The correct Answer is:C
IB=IA+Md2
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Multiple Correct9videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Linked Comprehension28videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 1EXERCISE - Subjective13videos
RIGID BODY DYNAMICS 1
- BOOK - CENGAGE PHYSICSCHAPTER - PROPERTIES OF SOLIDS AND FLUIDSEXERCISE - INTEGER_TYPE2videos
PROPERTIES OF SOLIDS AND FLUIDS
- BOOK - CENGAGE PHYSICSCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
Similar Questions
Let IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
View SolutionIn the figure shown, a planer body is in the shape of a rhombus ABCD: I1 and I2 are moment of inertias: about axis passing through centre and perpendicular to sides BC and DC respectively. I3 and I4 are amount of inertias about diagonal axis BD and AC respectively. Then the moment of inertia about an axis passing through centre and perpendicular tothe plane of body is given by
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
Let IAandIB be moments of inertia of a body about two axes A and B respectively. The axis A passes through the centre of massof the body but B does not. Choose the correct option.
AIA<IBBIA<IB, whether the axes are parallel or not parallelCif the axes are parallel IA<IBDIf the axes are not parallel IA≥IB - Question 2 - Select One
Let I1 and I2 be the moment of inertia of a uniform square plate about axes APC and OPO respectively as shown in the figure.P is centre of square. The ratio I1I2 moment of inertia is -
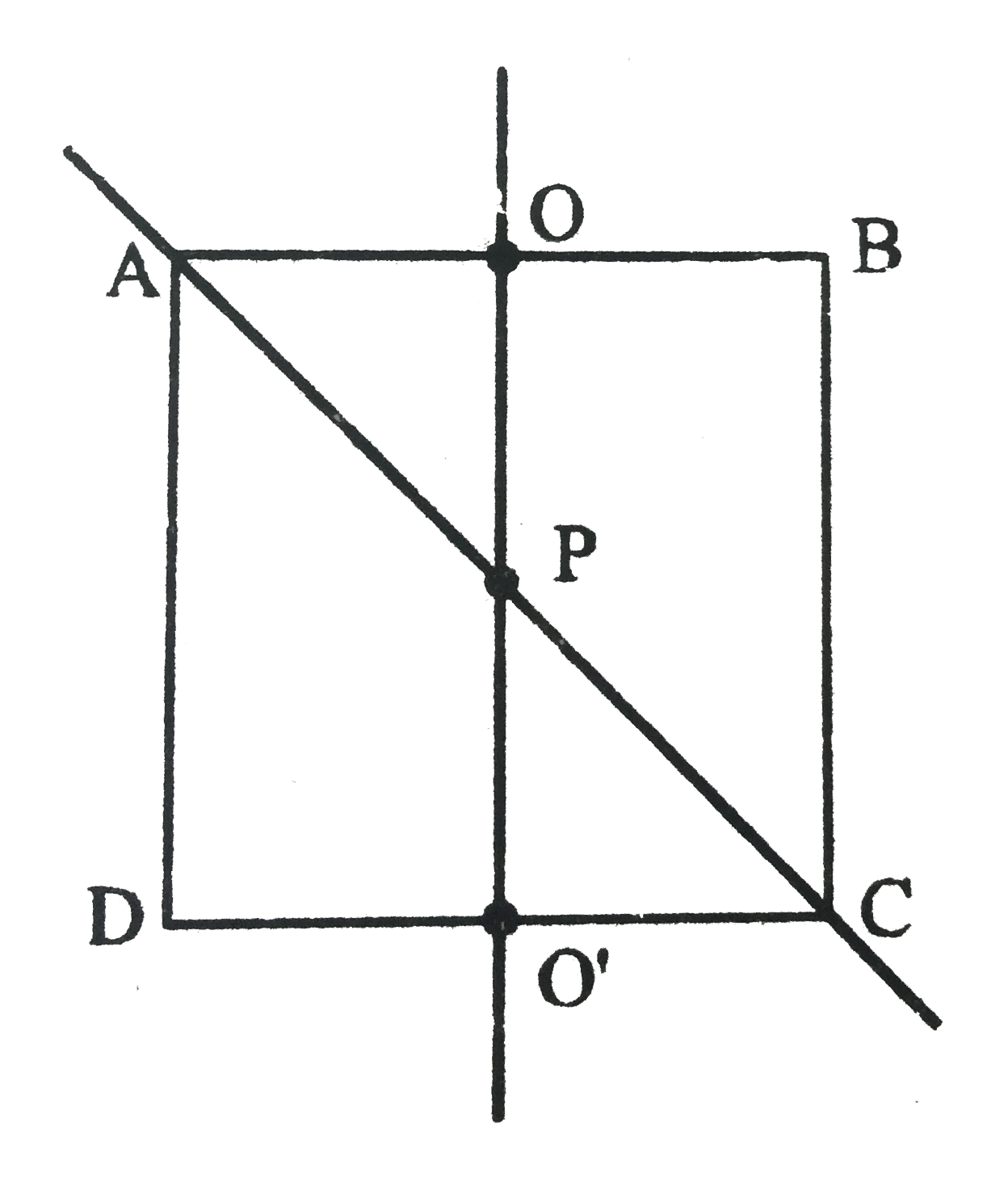 .A12√2B2C12D1
.A12√2B2C12D1 - Question 3 - Select One
If I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mas and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
Al1l2=3π2Bl1l2=2π2Cl1l2=π22Dl1l2=π23
If I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia of the ring about an axis perpendicular to plane of ring and passing through its centre formed by bending the rod, then
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown
 View Solution
View Solutionfind moment of inertia about an axis yy which passes through the centre of mass of the two particle system as shown
 View Solution
View SolutionIf I1 is the moment of inertia of a thin rod about an axis perpendicular to its length and passing through its centre of mass and I2 is the moment of inertia (about central axis) of the ring formed by bending the rod, then the ratio of I1 to I2 is
View SolutionThe moment of inertia of a solid cylinder of mass M, length 2R and radius R about an axis passing through the centre of mass and perpendicular to the axis of the cylinder is I1 and about an axis passing through one end of the cylinder and perpendicular to the axis of cylinder is I2
View Solution

