Let there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle A starts with a velocity v1 towards line AB, particle B starts with the velocity v2, towards line BC and particle C starts with velocity v3 towards line CA. Find the displacement of the centre of mass of the three particles A,B and C after time t. What would it be if v1=v2=v3?
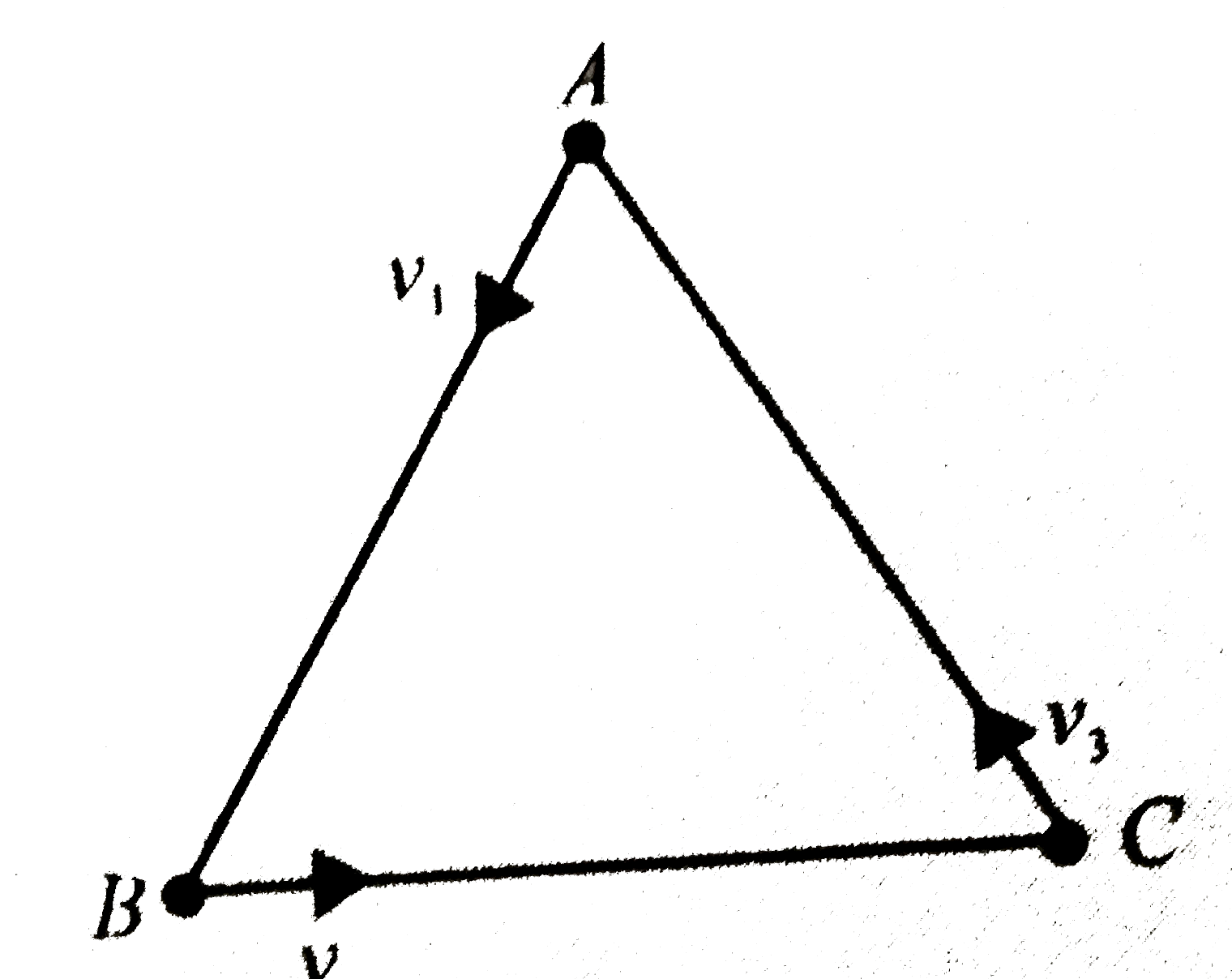
Step by step video & image solution for Let there are three equal masses situated at the vertices of an equilateral triangle, as shown in Fig. Now particle A starts with a velocity v_(1) towards line AB, particle B starts with the velocity v_(2), towards line BC and particle C starts with velocity v_(3) towards line CA. Find the displacement of the centre of mass of the three particles A, B and C after time t. What would it be if v_(1)=v_(2)=v_(3)? by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Practive Exercise
28 Videos
- LINEAR MOMENTUM & ITS CONSERVATIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - LINEAR MOMENTUM & ITS CONSERVATIONEXERCISE - Discussio Q
28 Videos
- KINEMATICSBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - KINEMATICSEXERCISE - Unsolved Numerical Pro.
83 Videos
- NEWTONS LAWS OF MOTIONBOOK - PHYSICS GALAXY - ASHISH ARORACHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - Unsolved Numerical Problem
81 Videos
Similar Questions
A particle moves with a velocity v(t)=(12)kt2 along a straight line . Find the average speed of the particle in a time t.
View SolutionThree particles A,B,andC are situated at the vertices of an equilateral triangle of side r at t=0. The particle A heads towards B, B towards C, C towards A with constant speeds v. Find the time of their meeting.
View Solution
Knowledge Check
Three particles of equal masses are placed at the corners of an equilateral triangle as shown in the figure. Now particle A starts with a velocity v1 towards line AB, particle B starts with a velocity v2 towards line BC and particle C starts with velocity v3 towards line CA. The displacement of CM of three particle A,B and C after time t will be (given if v1=v2=v3)
 AzeroBv1+v2+v33tCv1+√32v2+v323tDv1+v2+v34t
AzeroBv1+v2+v33tCv1+√32v2+v323tDv1+v2+v34tThree particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of
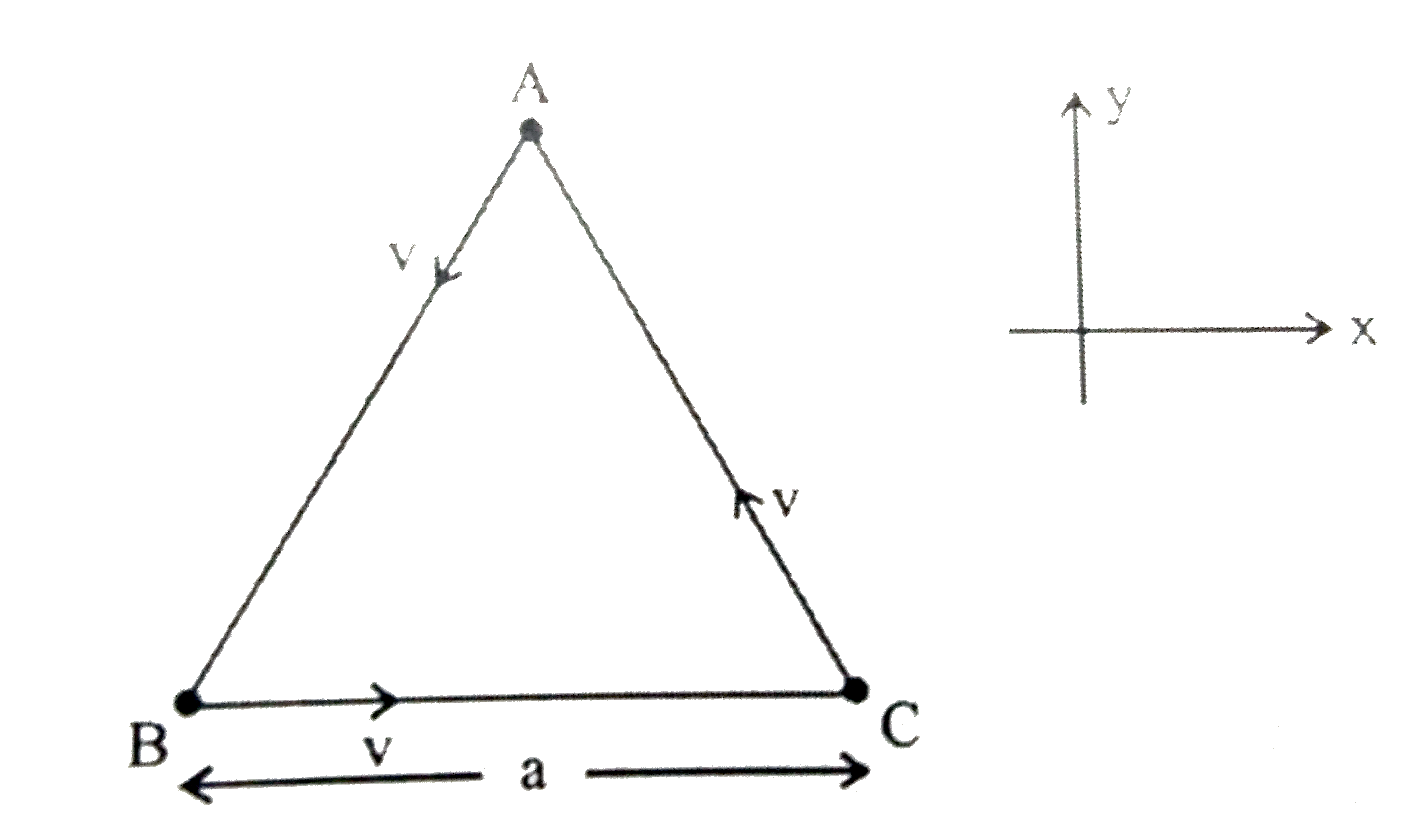 AAwrt.Bis=vcos30∘a in z-directionBBwrt.Cis=vcos30∘a in z-directionCAwrt.Cis=vcos30∘a in z-directionDBwrt.Ais=vcos30∘a in z-direction
AAwrt.Bis=vcos30∘a in z-directionBBwrt.Cis=vcos30∘a in z-directionCAwrt.Cis=vcos30∘a in z-directionDBwrt.Ais=vcos30∘a in z-directionTwo identical particles move towards each other with velocity 2v and v, respectively. The velocity of the centre of mass is:
AvBv/3Cv/2Dzero
The acceleration of a particle varies with time t as
a=t2+t+2
where t is in seconds.
The particle starts with an initial velocity v-3m/s at t=0. find the velocity of the particle at the end of 5s.
View SolutionTwo identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionA particle of mass m has a velocity −v0i, while a second particle of same mass has a velocity v0j. After the particles collide, first particle is found to have a velocity −12v0¯i then the velocity of othe particle is
View SolutionThree particles A,B and C and situated at the vertices of an equilateral triangle ABC of side of length l at time t=0,Each of the particles move with constant speed u. A always has its velocity along AB,B along BC and C along CA.
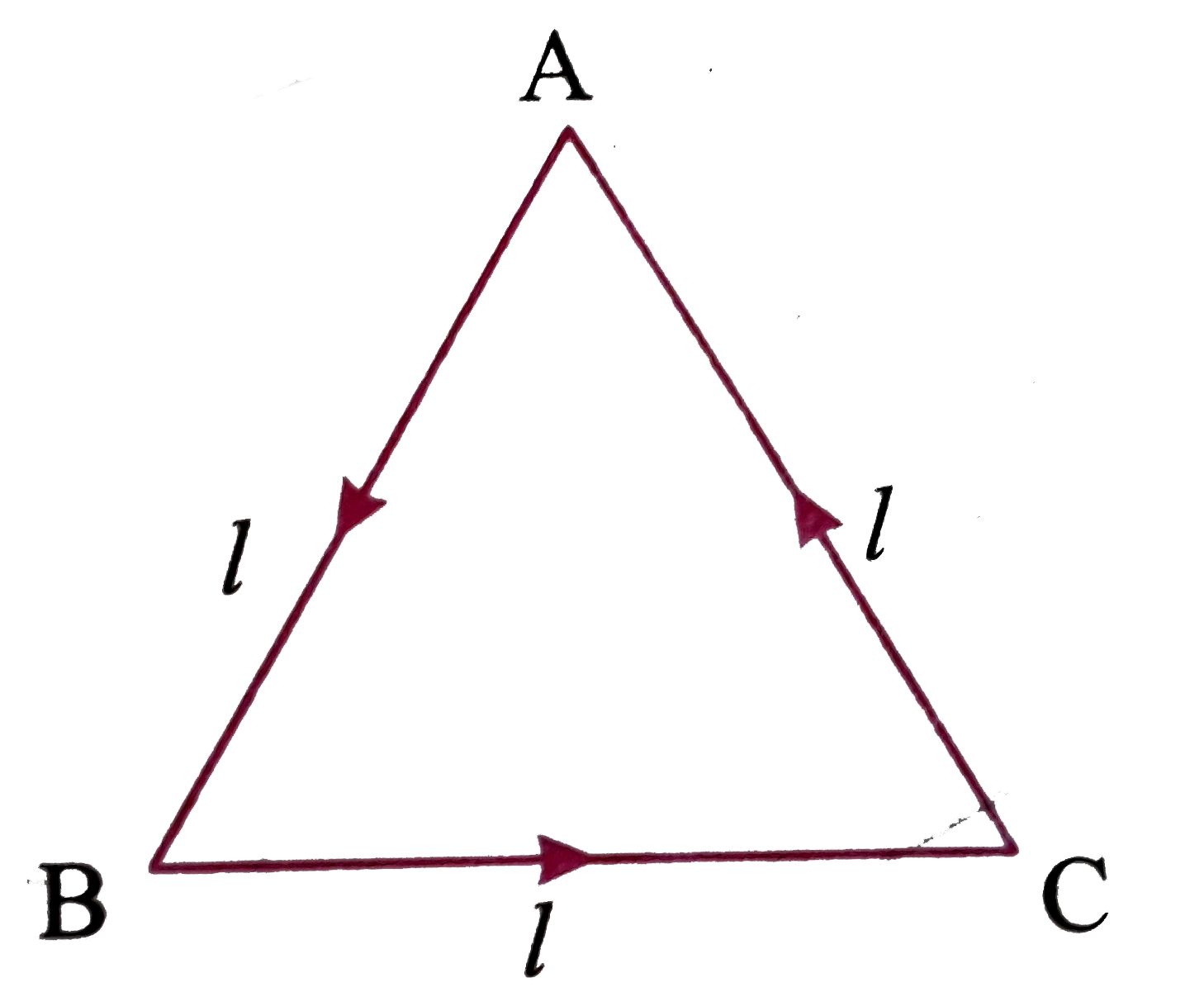
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View Solution
