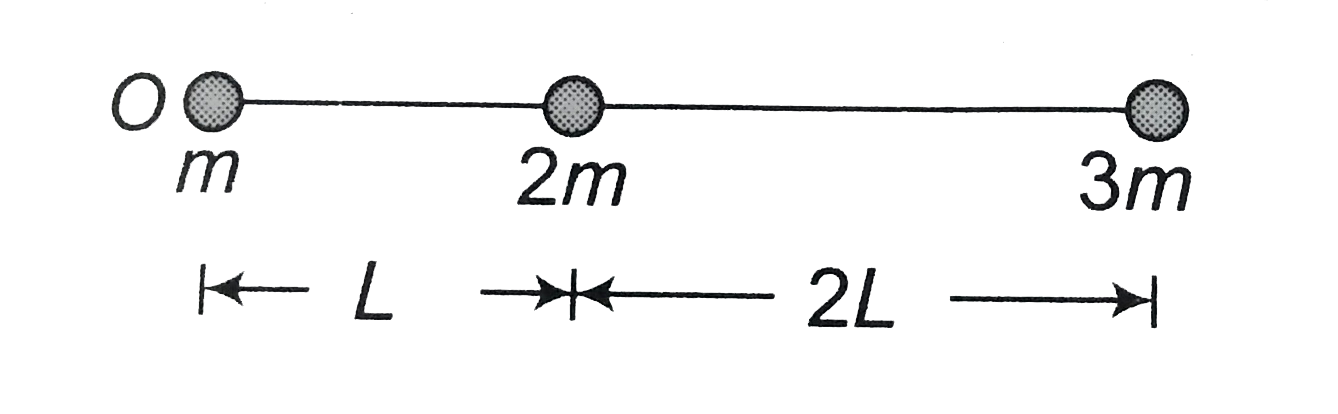
Locate the center of mass.

(a) Take location of the leftmost particle as origin.
xm02mL3mL+2L=3L
xc.m.=m1×0+m2×dm1+m2=m2dm1+m2
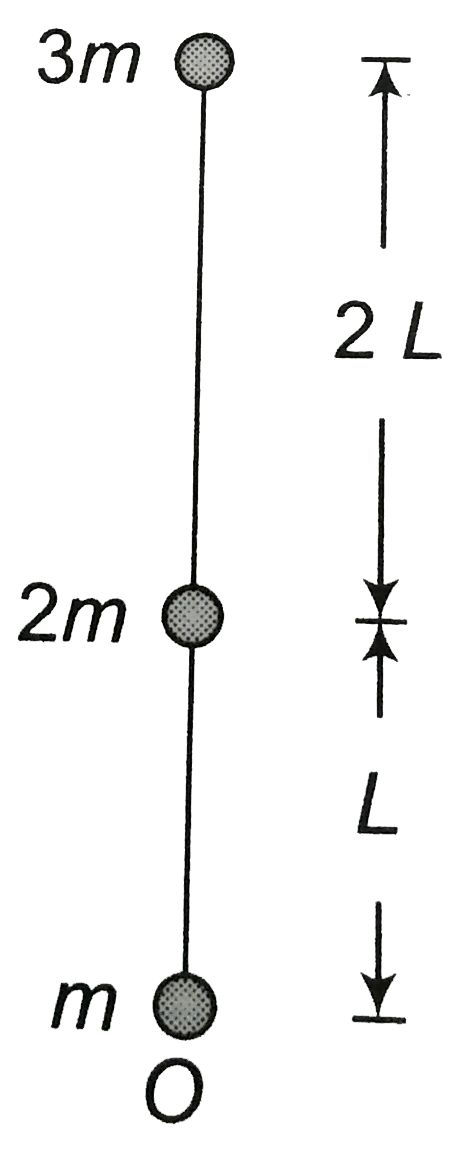
( c) Take the bottommost particle as origin.
ym02mL3mL+2L=3L
yc.m.=m×0+2m×L+3m×3Lm+2m+3m=11mL6m=11L6

Topper's Solved these Questions
Similar Questions
Knowledge Check
Assertion: If there are no external forces, the center of mass of a double star moves like a free particle.
Reason: If we go to the center of mass frame, then we find that the two stars are moving in a circle about the center of mass, which is at rest.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is not the correct explanation of assertionCIf assertion is true but reason is false.DIf both assertion and reason are false.The coordinates of the center of mass of the following quarter circular arc are
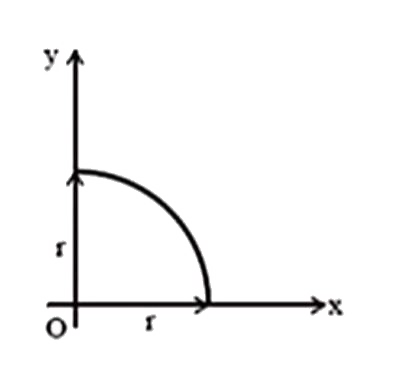 A(r2,r2)B(2r3,2r3)C(2rπ,2rπ)D(4rπ,4rπ)
A(r2,r2)B(2r3,2r3)C(2rπ,2rπ)D(4rπ,4rπ)Two balls are thrown simultaneously from top of tower in air as shown in the figure.
(i) The acceleration of the center of mass of two balls while in air is equal to g.
(ii) The path followed by the center of mass is parabola.
(iii) The path followed by the center of mass will change if one ball after striking the ground comes to rest.
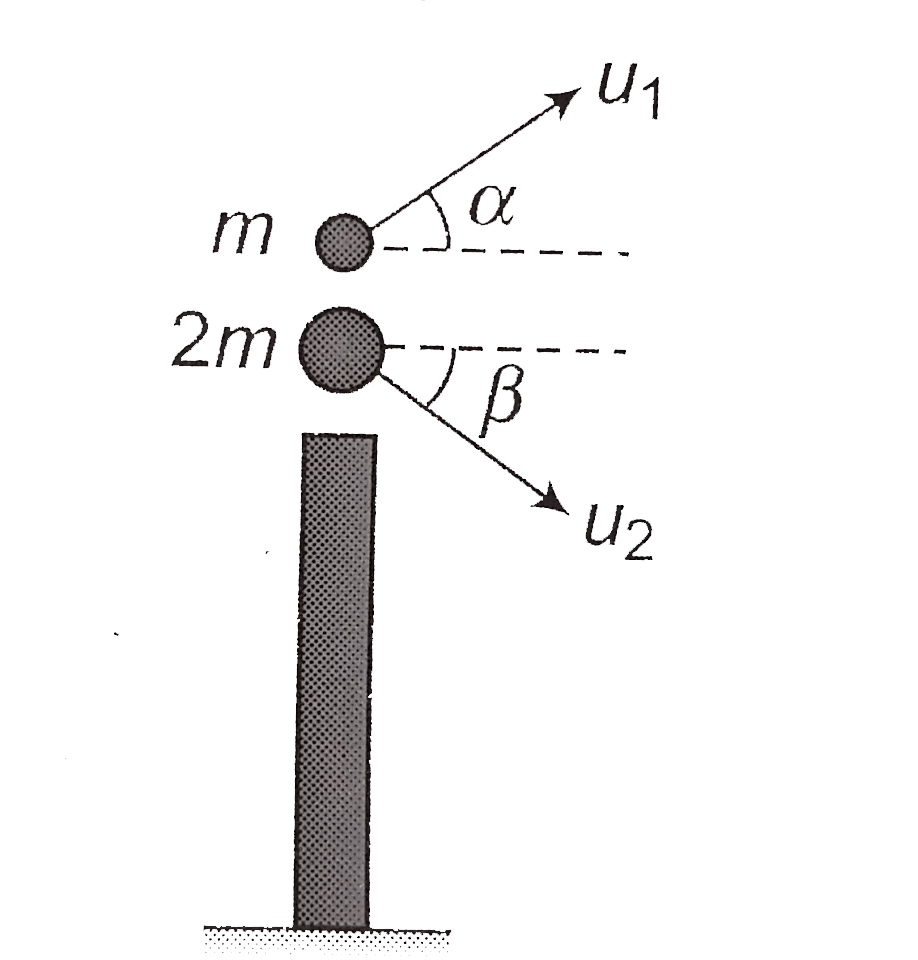 A(i),(ii),(iii)B(i),(ii),(iv)C(i),(ii)Dall of the above
A(i),(ii),(iii)B(i),(ii),(iv)C(i),(ii)Dall of the above
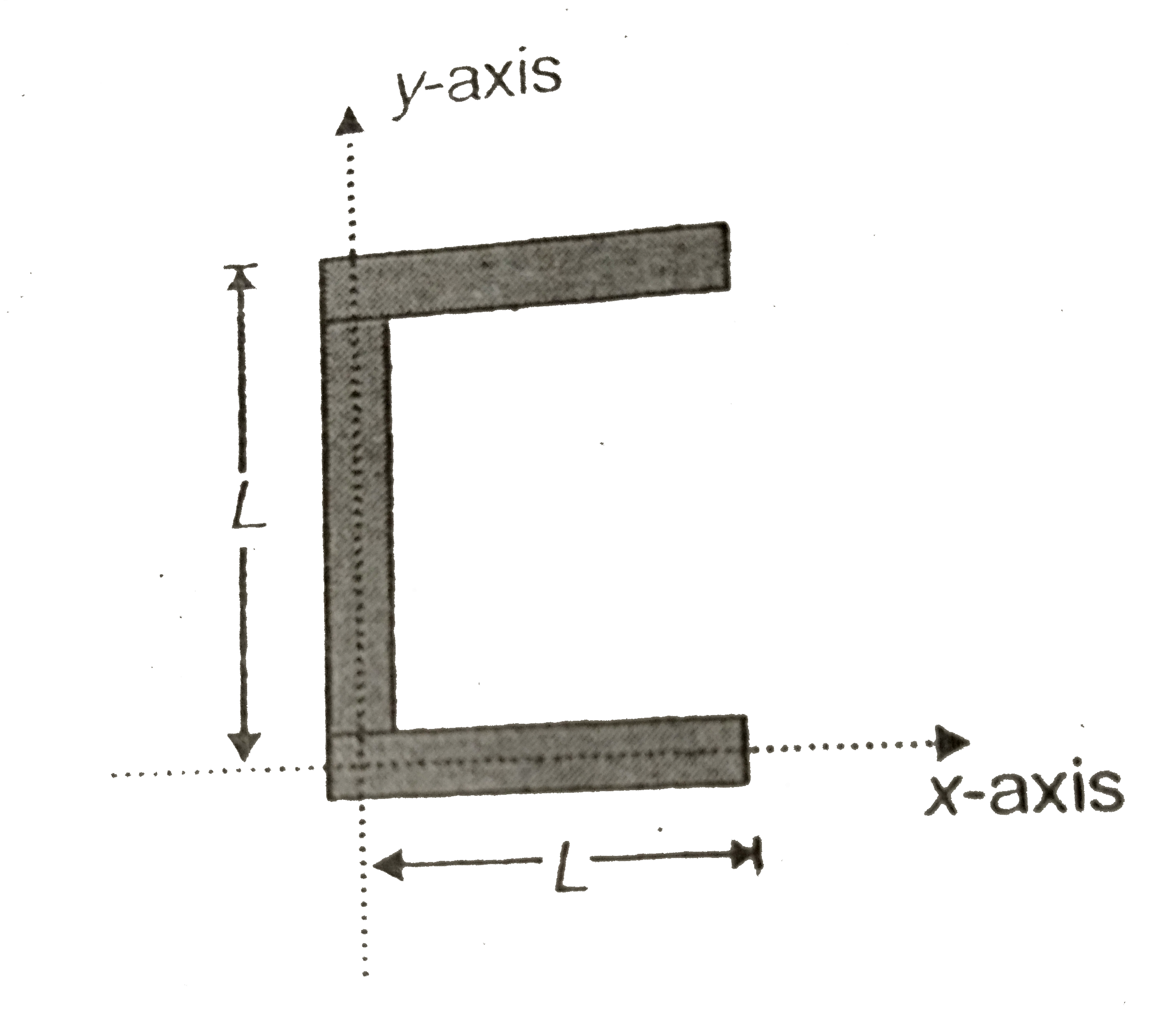
Locate the centre of mass of arrangement shown in figure. The three rods are identical in mass and length
View SolutionThree masses 3,4 and 5 kg are located at the corners of an equilateral triangle of side 1m. Locate to centre of mass of the system.
View SolutionFind the Xcm of center of mass of a barbell consisting of 50kg and 80kg weights at the opposite ends of a 1.5-along bar of negligible mass.
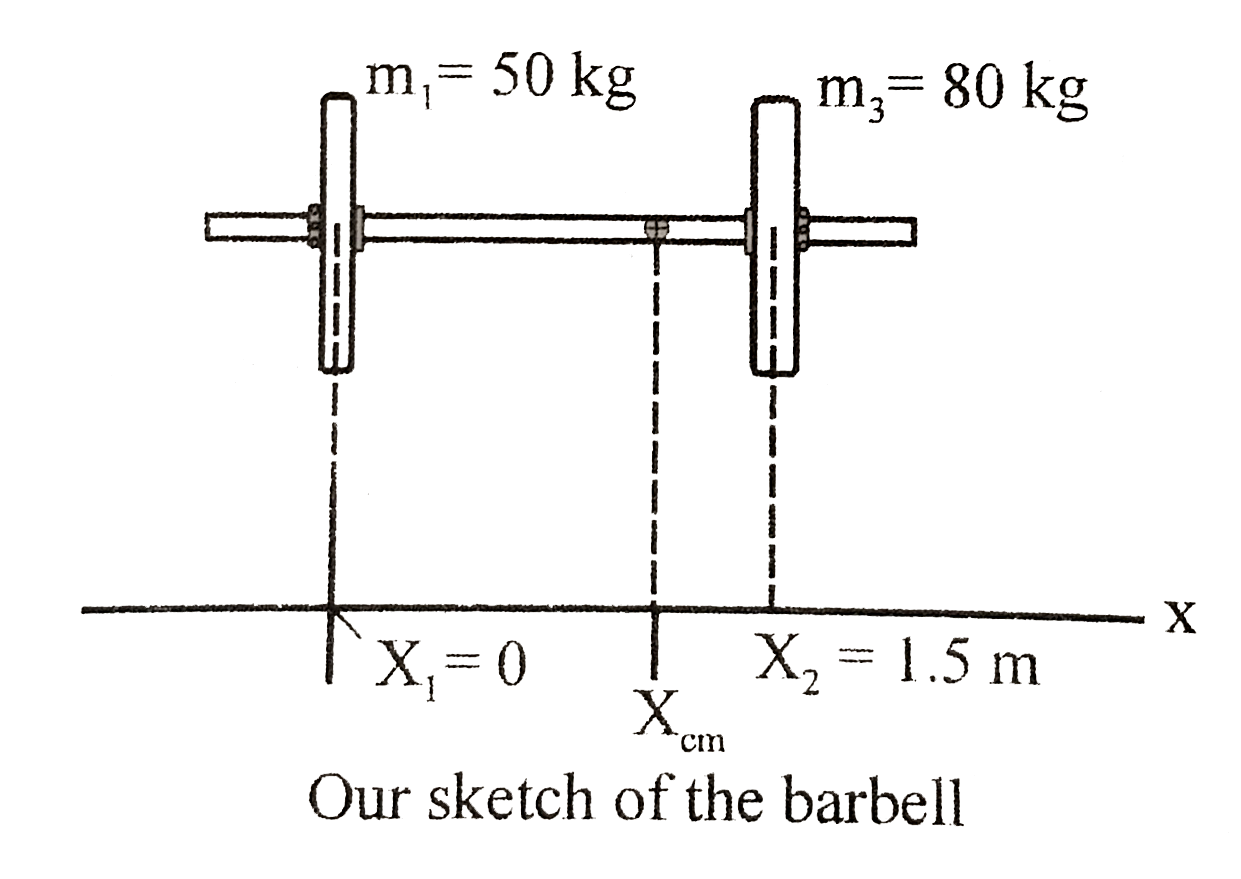
[Hint] Choosing the origin at one the masses here conveniently makes one of the terms in the sum Σmixizero. But, as always, the choice of origin is purely for convenience and doesn't influence that actual physical location of the center of mass.
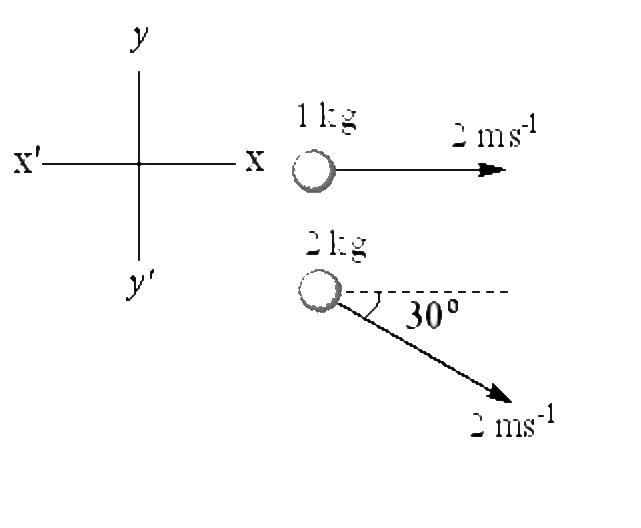
View SolutionFind the velocity of the center of mass of the system shown in the figure .
View SolutionThe velocities of two particles of masses m1 and m2 relative to an observer in an inertial frame are v1 and v2. Determine the velocity of the center of mass relative to the observer and the velocity of each particle relative to the center of mass.
View Solution
