 ltBrgt A block is attached to the end of a linear spring, the other end of which is anchored to a wall. The block is oscillating between extreme positions X and Y on a frictionless table, and when the block is at Point O, the spring is at its natural length. the value of the spring's force constant, k, is known, but the mass of the block, m, is unknown
ltBrgt A block is attached to the end of a linear spring, the other end of which is anchored to a wall. The block is oscillating between extreme positions X and Y on a frictionless table, and when the block is at Point O, the spring is at its natural length. the value of the spring's force constant, k, is known, but the mass of the block, m, is unknown
Q. If ω=√km, and the distance between O and Y is d, what is the speed of the block at point O?
dω2
dω
2dω
d2ω
The correct Answer is:B
When the block is at point Y, all its energy is due to the potential energy of the stretched spring, which is 12kd2. At the moment the block passes through the equilibrium position, O, this energy has been converted entirely to kinetic. By setting 12mv2 equal to 12kd2, we find that
12mv2=12kd2⇒v=d√k/m=dω.
Topper's Solved these Questions
Similar Questions
A block weighing 10N is attached to the lower end of a vertical spring (k =200N/m), the other end of which is attached to a ceiling. The block oscillates vertically and has a kinetic energy of 2.0J as it passes through the point at which the spring is unstretched. The amplitude of the oscillation of block is
View SolutionThe block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View Solution
Knowledge Check
A block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
A2mgμkBmgμkC4mgμkDNone of theseA block is attached to a spring of stiffness k. The other end of the spring is attached to a fixed wall. The entire system lie on a horizontal surface and the spring is in natural state. The natural length of the springs is l0 if the block is slowly lifted up vertically to a height 512l0 from its initial position :
AThe work done by the lifting force =kl20288+512mgl0BThe work done by the spring force =kl20288CThe work done by the gravity =512mgl0DThe work done by lifting force =−512mgl0+kl20288In the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.
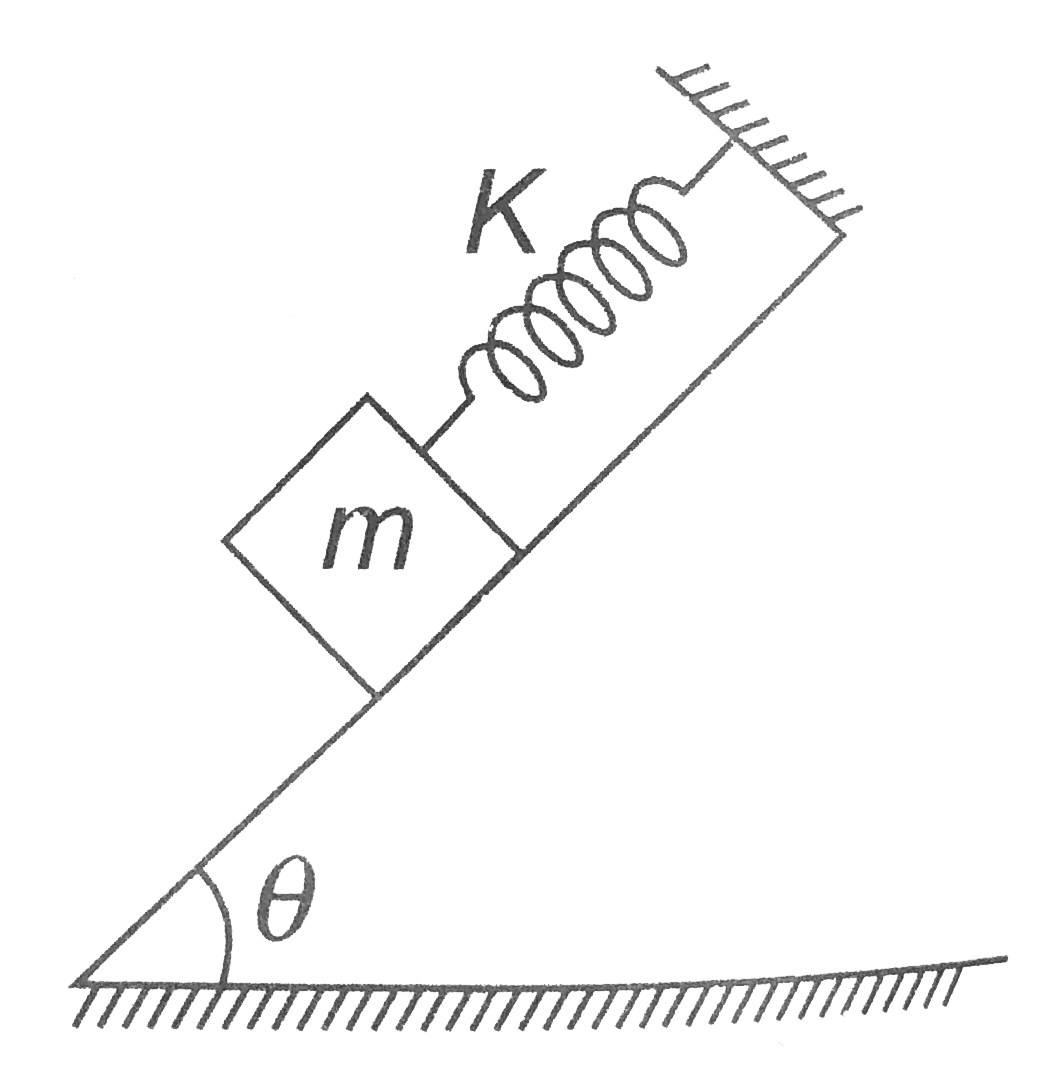 A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk
A(cosθ+μsinθ)g√mkB(cosθ−μsinθ)g√mkC(sinθ+μcosθ)g√mkD(sinθ−μcosθ)g√mk
The block of mass m is released when the spring was in its natrual length. Spring constant is k. Find the maximum elongation of the spring.

View SolutionA block of mass m is attached to one end of a mass less spring of spring constant k. the other end of spring is fixed to a wall the block can move on a horizontal rough surface. The coefficient of friction between the block and the surface is μ then the compession of the spring for which maximum extension of the spring becomes half of maximum compression is .
View SolutionIn the figure shown, a spring of spring constant K is fixed at on end and the other end is attached to the mass 'm' . The coefficient of friction between block and the inclined plane is μ. The block is released when the spring is in tis natural length. Assuming that the θ>μ, the maximum speed of the block during the motion is.

View SolutionA block of mass m is pushed against a spring of spring constant k fixed at the end to a wall. The block can side on a frictionless table as shown in figure. The natural length of the spring is L0 and it is compressed ti half its natural length when the block is relesed. Find teh velocity of the block aa s function of its distance x from the wall .

View SolutionThe left end of the spring tied to a wall and at the right end is attached to a block of mass m, which is placed on a frictionless ground. The force F displaces the block by distance x where it is exactly balanced by the spring force.
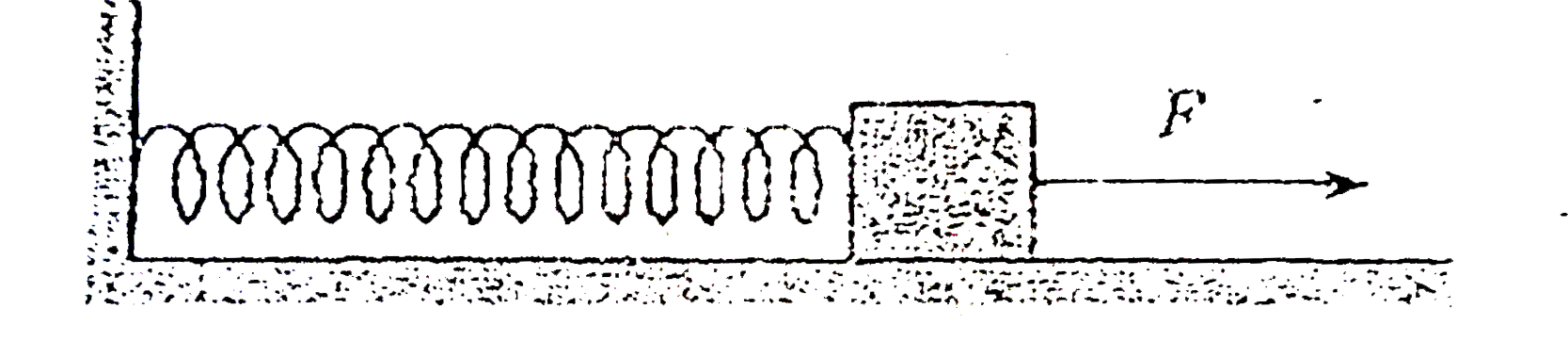
What is the maximum speed of the block in the ensuing motion after the force F is removed?
View Solution
