Magnetic poles always exist in pairs.
Step-by-Step Solution:
1. Understanding Magnetic Poles:
- A magnet has two distinct ends known as poles: the North Pole and the South Pole.
2. Magnetic Field Lines:
- Magnetic field lines are invisible lines that represent the direction and strength of the magnetic field. They emerge from the North Pole and enter the South Pole.
3. Existence of Poles:
- If we consider a magnet, regardless of its size, it will always have both a North Pole and a South Pole. This means that if you have a magnet, you cannot have just one pole without the other.
4. Reason for Pairing:
- The reason magnetic poles exist in pairs is that magnetic field lines must have a starting point (North Pole) and an endpoint (South Pole). If there were only a North Pole, the magnetic field lines would have nowhere to go, which is not possible.
5. Conclusion:
- Therefore, the statement "Magnetic poles always exist in pairs" is true. Every magnet, no matter how small, will always have both a North and a South Pole.
---
- A magnet has two distinct ends known as poles: the North Pole and the South Pole.
- Magnetic field lines are invisible lines that represent the direction and strength of the magnetic field. They emerge from the North Pole and enter the South Pole.
- If we consider a magnet, regardless of its size, it will always have both a North Pole and a South Pole. This means that if you have a magnet, you cannot have just one pole without the other.
- The reason magnetic poles exist in pairs is that magnetic field lines must have a starting point (North Pole) and an endpoint (South Pole). If there were only a North Pole, the magnetic field lines would have nowhere to go, which is not possible.
- Therefore, the statement "Magnetic poles always exist in pairs" is true. Every magnet, no matter how small, will always have both a North and a South Pole.
Topper's Solved these Questions
- MAGNETISMBook:ICSEChapter:MAGNETISMExercise:Exercises (Section I) Choose the correct option to fill in the blank.
Explore 9 Videos
- MAGNETISMBook:ICSEChapter:MAGNETISMExercise:Exercises (Section II) Give reason for the following
Explore 4 Videos
- MAGNETISMBook:ICSEChapter:MAGNETISMExercise:Exercises (Section I) Choose the correct option
Explore 8 Videos
- LIGHTBook:ICSEChapter:LIGHTExercise:Picture Based Questions
Explore 21 Videos
- MATTERBook:ICSEChapter:MATTERExercise:Picture Based Questions
Explore 2 Videos
Similar Questions
Assertion (A): It is not necessary that every magnet has one north pole and one south pole.
Reason (R ): It is a basic fact that magnetic poles occur in pairs
View SolutionSTATEMENT-1 : Magnetic poles are only mathematical assumptions and have no real existence .
and
STATEMENT-2 : Magnetic field lines are always in closed loops .
View Solution
Knowledge Check
Assertion : Gauss's law of magnetism is different from that for electrostatics.
Reason : Isolated magnetic poles are not known to exist.AIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true and reason is not the correct explanation of assertion.CIf assertion is ture but reason is false.DIf both assertion and reason are false.Statement-1 The net magnetic flux through a spherical surface enclosing north pole of a bar magnet as zero
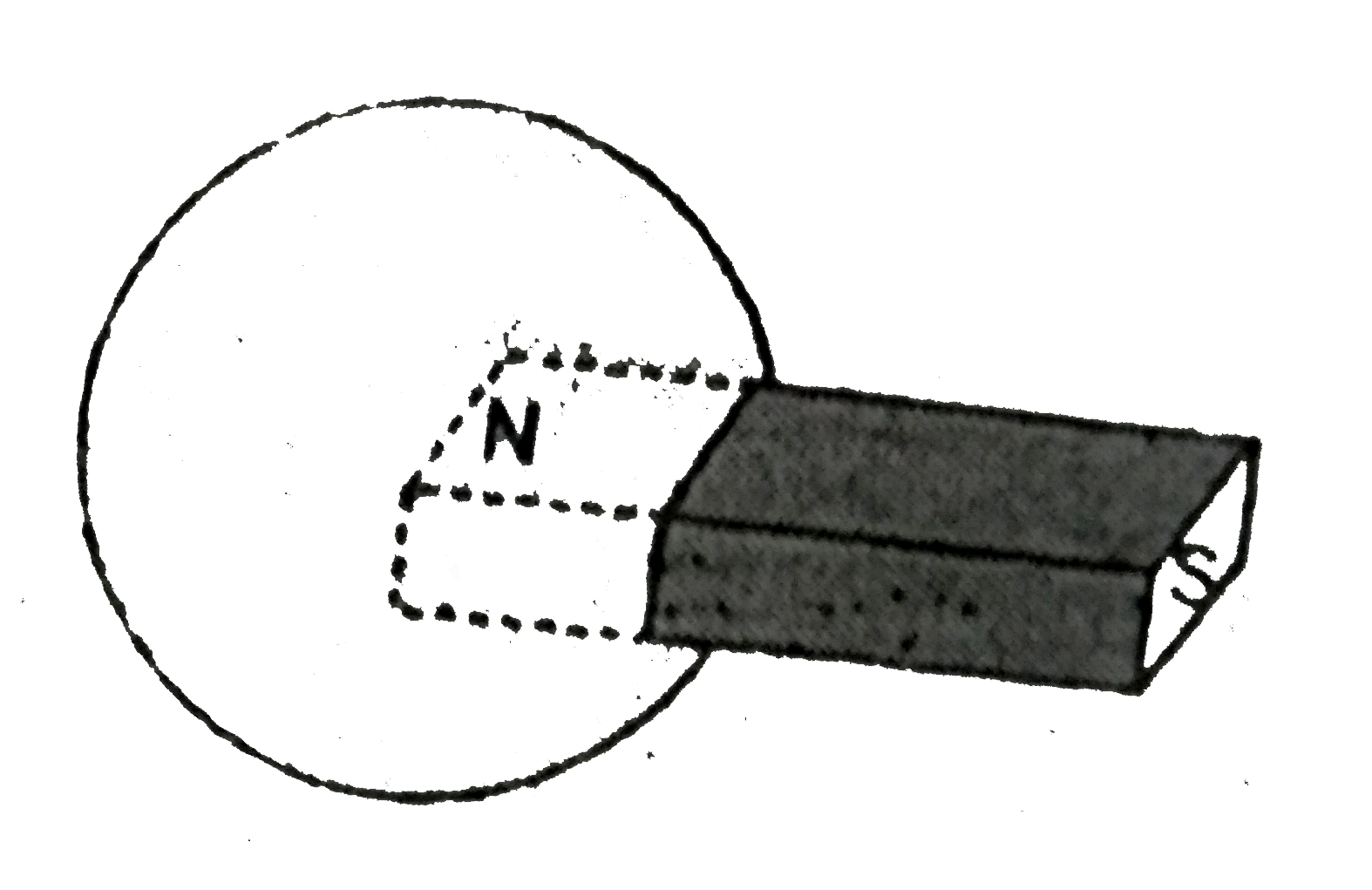
Statement-2 Magnetic field lines always form closed loopsAIf both assertion and reason are true and reason is the correct explanation of assertion.BIf both assertion and reason are true but reason is the correct explanation of assertion.CIf assertion is true but reason is falseDIf both assertion and reason are false.
Magnetic energy always causes attraction.(T/F)
View SolutionAssertion: Basic difference between an electric line and magnetic line of force is that former is discontinuous and the latter is continuous or endless.
Reason: No electric lines of force exist inside a charged body but magnetic lines do exist inside a magnet.
View SolutionThe magnetic pole that points towards the geographical South
View SolutionSTATEMENT-1 : Magnetic fluex linked with a closed surface is always zero .
and
STATEMENT-2 : Magnetic field can exist without North and South poles .
View SolutionDo two distinct poles actually exist at two nearby points in a magnetic dipole?
View SolutionStatement-1 The net magnetic flux through a spherical surface enclosing north pole of a bar magnet as zero

Statement-2 Magnetic field lines always form closed loops
View Solution
