Match the following :

Video Solution
Text Solution
The induction at C is
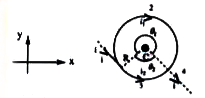
→B=→B1+→B2+→B3+→B4 …………. (i)
→B1=μ0i4πR⊙ ….(ii) −→B2=μ0i1θ14πR …(iii)
−→B3=μ0i2θ24πR⊙....(iv)→B4=0.....(v)
Using the above equations, we get
→B=μ04πR(i+i3θ2−i1θ1)⊙ (a)
Since, the branches 2 and 3 are in parallel,
i1R1=i2R2
Since, R1=pl1A=p(Rθ1)A and R2=pA(Rθ2)
i1θ1=i2θ2 ....(b)
using equations (a) and (b ), we get
B=μ0i4πR⊙
|
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IA
142 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH SERIESCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE-IB
71 Videos
- MOTION IN A STRAIGHT LINE BOOK - AAKASH SERIESCHAPTER - MOTION IN A STRAIGHT LINE EXERCISE - very Short answer type question
15 Videos
- NUCLEAR PHYSICSBOOK - AAKASH SERIESCHAPTER - NUCLEAR PHYSICSEXERCISE - ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
3 Videos
