Mercury is poured in a U-tube. Temperature of one side is 50∘C and level of mercury on this side is h2. Temperature of the other side of 100∘C and level of mercury on this side is h2. Then
h1=h2
h2<h1
h2>h1
h2=2h1
The correct Answer is:C
To solve the problem, we need to analyze the behavior of mercury in a U-tube when subjected to different temperatures on either side. Let's break down the steps:
1. Understanding the U-tube Setup:
- We have a U-tube filled with mercury.
- The left side is at a temperature of 50∘C and has a mercury level denoted as h1.
- The right side is at a temperature of 100∘C and has a mercury level denoted as h2.
2. Effect of Temperature on Density:
- The density of mercury decreases as the temperature increases. Therefore, the density at 50∘C (denoted as ρ1) is greater than the density at 100∘C (denoted as ρ2).
- Mathematically, we can express this as:
ρ1>ρ2
3. Applying Hydrostatic Pressure Principle:
- At the same horizontal level in the U-tube, the pressure exerted by the mercury column on both sides must be equal.
- The pressure exerted by the mercury on the left side can be expressed as:
P1=h1⋅ρ1⋅g
- The pressure exerted by the mercury on the right side can be expressed as:
P2=h2⋅ρ2⋅g
- Here, g is the acceleration due to gravity.
4. Setting the Pressures Equal:
- Since the pressures at the same level must be equal, we can set the two pressure equations equal to each other:
h1⋅ρ1⋅g=h2⋅ρ2⋅g
- The g cancels out from both sides:
h1⋅ρ1=h2⋅ρ2
5. Rearranging the Equation:
- We can rearrange the equation to find the relationship between h1 and h2:
h1h2=ρ2ρ1
6. Interpreting the Result:
- Since ρ1>ρ2, it follows that:
ρ2ρ1<1
- Therefore, we conclude that:
h1<h2
Final Conclusion:
The height of mercury on the side with 50∘C (h1) is less than the height on the side with 100∘C (h2).
- We have a U-tube filled with mercury.
- The left side is at a temperature of 50∘C and has a mercury level denoted as h1.
- The right side is at a temperature of 100∘C and has a mercury level denoted as h2.
- The density of mercury decreases as the temperature increases. Therefore, the density at 50∘C (denoted as ρ1) is greater than the density at 100∘C (denoted as ρ2).
- Mathematically, we can express this as:
ρ1>ρ2
- At the same horizontal level in the U-tube, the pressure exerted by the mercury column on both sides must be equal.
- The pressure exerted by the mercury on the left side can be expressed as:
P1=h1⋅ρ1⋅g
- The pressure exerted by the mercury on the right side can be expressed as:
P2=h2⋅ρ2⋅g
- Here, g is the acceleration due to gravity.
- Since the pressures at the same level must be equal, we can set the two pressure equations equal to each other:
h1⋅ρ1⋅g=h2⋅ρ2⋅g
- The g cancels out from both sides:
h1⋅ρ1=h2⋅ρ2
- We can rearrange the equation to find the relationship between h1 and h2:
h1h2=ρ2ρ1
- Since ρ1>ρ2, it follows that:
ρ2ρ1<1
- Therefore, we conclude that:
h1<h2
The height of mercury on the side with 50∘C (h1) is less than the height on the side with 100∘C (h2).
Topper's Solved these Questions
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced
57 Videos
- PROPERTIES OF MATTERBOOK - DC PANDEY ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - More than one option is correct
21 Videos
- PROJECTILE MOTIONBOOK - DC PANDEY ENGLISHCHAPTER - PROJECTILE MOTIONEXERCISE - Level - 2 Subjective
10 Videos
- RAY OPTICSBOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Integer type q.
14 Videos
Similar Questions
Mercury has an angle of contact of 120∘ with glass. A narrow tube of radius 1.0mm made of the glass is dipped in a through containing mercury. By what amount does the mercury dip down in the tube relative to the liquid surface outside. Surface tension of mercury at the temperature of the experiment os 0.5N/m and density of mercury is 13.6×103kg/m3.
(Take g=9.8m/s2).
View SolutionThe hypotenuse of a triangle is 2.5 cm. If one of the sides is 1.5 cm. find the length of the other side.
View SolutionThe readings of a thermometer at 0∘C and 100∘C are 50cm and 75cm of mercury column respectively. Find the temperature at which its reading is 80cm of mercury column ?
View SolutionThe readings of a thermometer at 0∘C and 100∘C are 50cm and 75cm of mercury column respectively. Find the temperature at which its reading is 80cm of mercury column ?
View SolutionTwo identical glass spheres filled with air are connected by a thin horizontal glass tube the glass tube contains a pellet of mercury at its mid-point Air in one sphere is at 0∘C and the other is at 20∘C if temperature of both the vessels are increased by 10∘C then neglecting the expansions of the bulbs and the tube
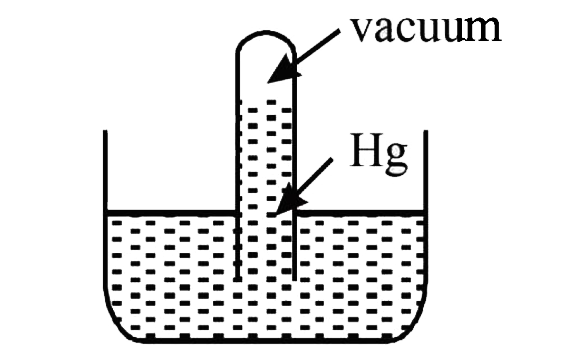
View SolutionA barometer made of very narrow tuve (see fig) is placed at normal temperature and pressure. The coefficient of volume expansion of mercury is 0.00018perC∘ and that of the tube is negligible. The temperature of mercury in the barometer is now raised by 1∘C, but the temperature of the atmosphere does not raised by 1∘C, but the temperature of the atmosphere does not change. Then the mercury height in the tube remains unchanged.
View SolutionIf one side of the square is 2x−y+6=0, then one of the vertices is (2,1) . Find the other sides of the square.
View SolutionIf one side of the square is 2x−y+6=0, then one of the vertices is (2,1) . Find the other sides of the square.
View SolutionA quantity of gas is collected in a gradutated tube over the mercury. The volume of the gas at 20∘C is 50.0mL and the level of the mercury in the tube is 100mm above the outside mercury level. The barometer reads 750mm. Volume at STP is
View SolutionA horizontal uniform glass tube of 100cm length is sealed at both ends contains 10cm mercury column in the middle , the temperature and pressure of air on either side of mercury column are repectively 31∘C and 76cm of mercury, if the air column at one end is kept at0∘C and the other end at 273∘C then pressure if air which is 0∘C is
(in cm of Hg)
View Solution
