Mole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K (figure). One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it .At any given time.
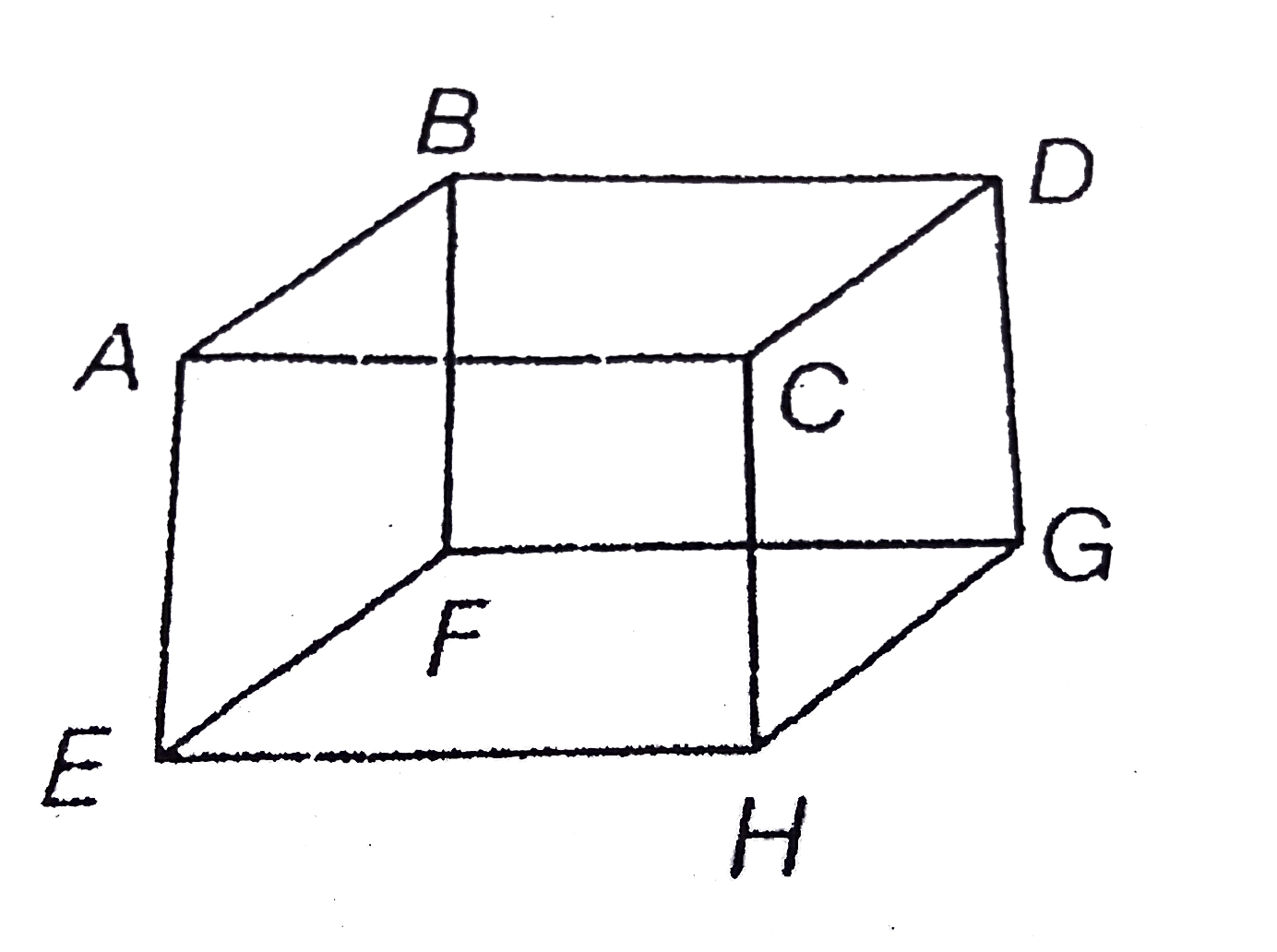
the pressure on EFGH would be zero
the pressure on all the faces will be equal
the pressure on EFGH would be double the pressure on ABCD
the pressure on EFGH would be half that on ABCD
The correct Answer is:D
When a moving molecule colloides elastically with the wall of the container, the momentum transformed by the molecule to the wall = mv - (-mv) = 2mv.
Force exerted by the molecule on the wall = Rate of change of momentum and pressure =ForceArea.
This is for a normal surface of the cube.
But only the face EFGH is a totally absorbing surface. Hence only the momentum mv is transformed to it (instead of 2mv for the other surfaces).
∴ The pressure on EFGH = 12 of the pressure on ABCD.
Topper's Solved these Questions
- KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATIONBOOK - MARVEL PUBLICATIONCHAPTER - KINETIC THEORY OF GASES ,THERMODYNAMICS AND RADIATIONEXERCISE - TEST YOUR GRASP - 9
30 Videos
- INTERFERENCE AND DIFFRACTIONBOOK - MARVEL PUBLICATIONCHAPTER - INTERFERENCE AND DIFFRACTIONEXERCISE - TEST YOUR GRASP
20 Videos
- MAGNETIC EFFECTS OF ELECTRIC CURRENTBOOK - MARVEL PUBLICATIONCHAPTER - MAGNETIC EFFECTS OF ELECTRIC CURRENTEXERCISE - MCQ
195 Videos
Similar Questions
The internal energy (U) of an ideal gas is plotted against volume for a cyclic process ABCDA, as shown in the figure.
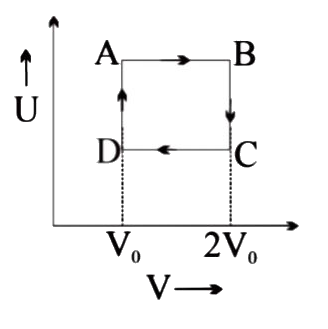
The temperature of the gas at B and C are 500 K and 300 K, respectively. The heat absorbed by the gas (in cal/mol) in this cyclic process, is :
View SolutionTwo moles of a certain ideal gas at 300K were cooled at constant volume so that the pressure was reduced to half t he initial value. Then, as a result of heating at constant pressure, the gas expanded till its temperature got back ot the initial value. Find the total amount of heat absorbed by the gas in the process.
View Solution
Knowledge Check
Mole of an ideal gas is contained in a cubical volume V, ABCDEFGH at 300 K (figure). One face of the cube (EFGH) is made up of a material which totally absorbs any gas molecule incident on it .At any given time.
 AThe pressure on EFGH would be zero.Bthe pressure on all the faces will the equalCthe pressure of EFGH would be double the pressure on ABCD.DThe pressure on EFGH would be half that on ABCD.
AThe pressure on EFGH would be zero.Bthe pressure on all the faces will the equalCthe pressure of EFGH would be double the pressure on ABCD.DThe pressure on EFGH would be half that on ABCD.One mole of an ideal gas is expanded freely and isothermally at 300K from 5L to 10L volume. If ΔE=0, then ΔH is
AzeroB5×300 calC5 calD−2×5×300 calOne mole of O2 gas is contained in a box of volume V=2m3 at pressure P0 and temperature 300K The gas is now heated to 600 K and the molecules now get dissociated into oxygen atoms. The new pressure of the gas is
AP0B2P0C4P0D8P0
One mole of an ideal gas is expanded isothermally at 300 K until its volume is tripled . Find the values of ΔSsys under the condition.
View SolutionTwo moles of an ideal monoatomic gas occupy a volume 2V at temperature 300K, it expands to a volume 4V adiabatically, then the final temperature of gas is
View Solution1 mole of H2 gas is contained in box of volume V=1.00m3atT=300K. The gas is heated to a temperature of T = 3000 K and the gas gets converted to a gas of hydrogen atoms. The final pressure would be (considering all gases to be ideal)
View Solution1 mole of H2 gas in contained in a box of volume V 1.00 m3 at T =300 K. The gas is heated to a temperature of T= 3000K and the gas gets converted to a gas of hydrogen atoms. The final pressure would be (considering all gases to be ideal)
View SolutionOne mole of an ideal gas expands at a constant temperature of 300 K from an initial volume of 10 litre to a final volume of 20 litre.The work done in expanding the gas is
View Solution
