Monochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is μ, a ray, incident at an angle θ, on the face AB would get transmitted through the face AC of the prism provided:
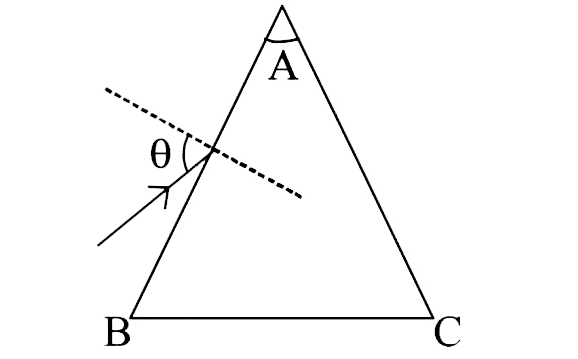
θ>sin−1[μsin(A−sin−1(1μ))]
θ<sin−1[μsin(A−sin−1(1μ))]
θ>cos−1[μsin(A−sin−1(1μ))]
θ<cos−1[μsin(A−sin−1(1μ))]
The correct Answer is:A
Here, μ=sini1sinr1,Asi1=θ
sinθ=μsinr1
or sinr1=sinθμ or r1=sin−1(sinθμ)
As r1+r2=A,
∴r2=A−r1 or r2=A−sin−1(sinθμ)
This shows, r2<sin−1(1μ)
A−sin−1(sinθμ)<sin−1(1μ)
or A−sin−1(1μ)<sin−1(sinθμ)
or sin(A−sin−1(1μ))<sinθμ
or μ×sin(A−sin−1(1μ))<sinθ
or θ>sin−1[μsin{A−sin−1(1μ)}].
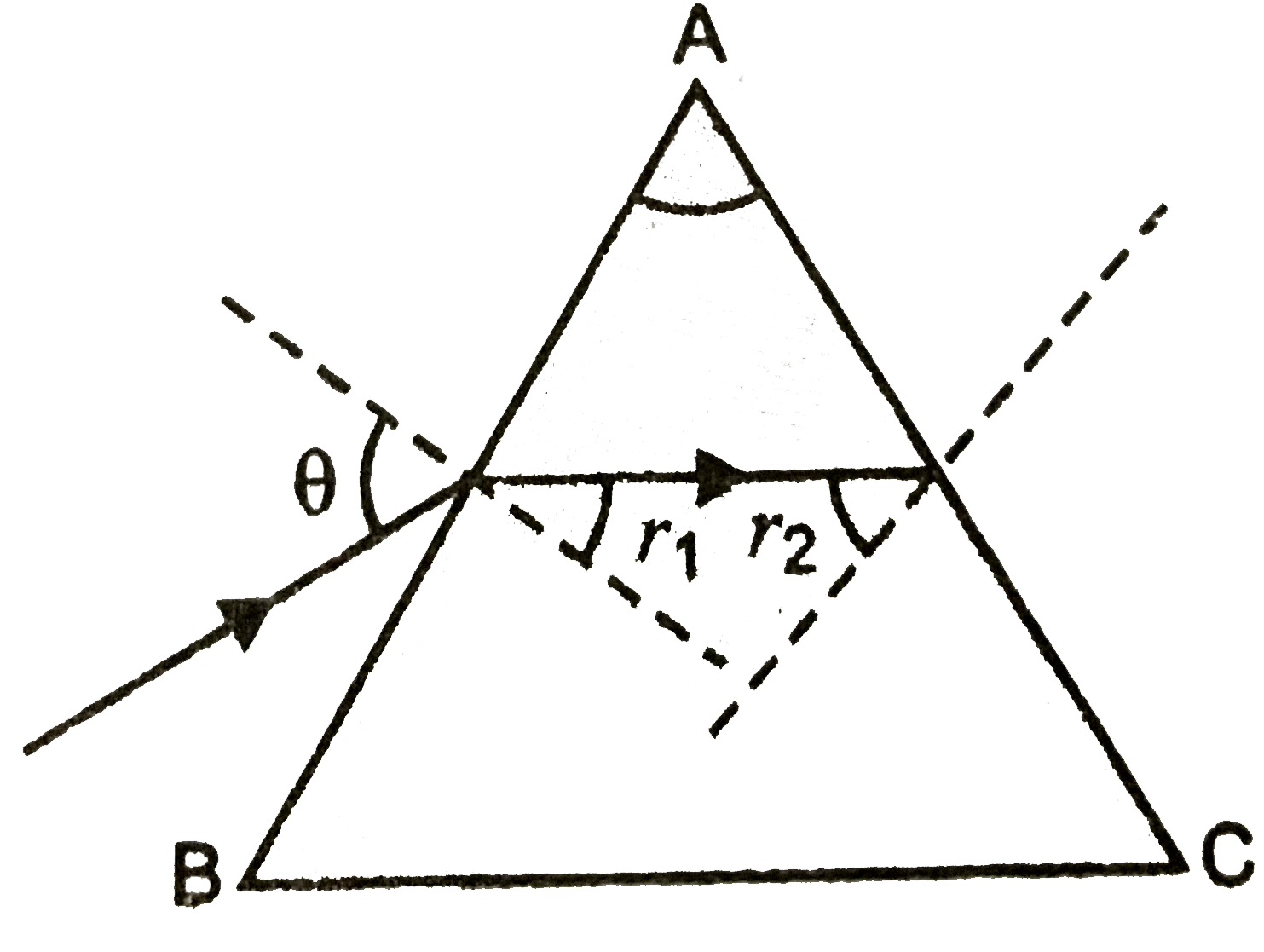 .
.
Topper's Solved these Questions
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - (Competition)Comprehension
7 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - Integer Question
4 Videos
- RAY OPTICSBOOK - PRADEEPCHAPTER - RAY OPTICSEXERCISE - (Exemplar) Multiple choice
16 Videos
- PROPERTIES OF BULK MATTERBOOK - PRADEEPCHAPTER - PROPERTIES OF BULK MATTEREXERCISE - Multiple choice questions
7 Videos
- SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONBOOK - PRADEEPCHAPTER - SYSTEMS OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assertion- Reason Type questions
20 Videos
Similar Questions
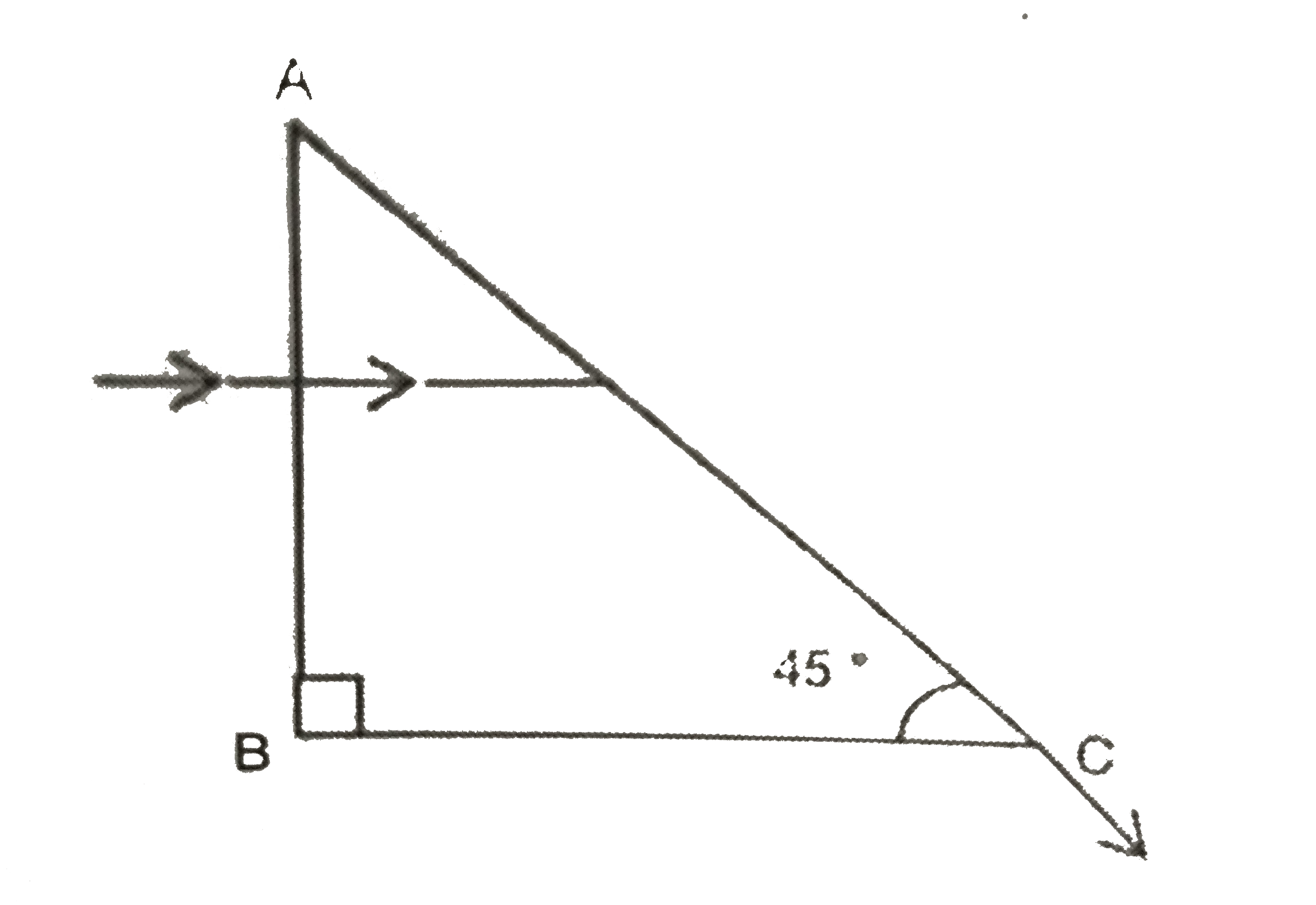
What is the refractive index of the material of the glass prism shown in the figure, if a ray of light incident normally at the face AB emerges along the face AC?
View SolutionThe refractive index of a prism is μ. Find the maximum angle of the prism for which a ray incident on it will be transmitted through other face without total internal reflection.
View Solution
Knowledge Check
A ray of light incident on a prism of angle 60∘, does not emerge out. Refractive index of material of prism may be
A1.50B2.30C1.80D1.20Refractive index of a prism is √7/3 and the angle of prism is 60∘. The minimum angle of incidence of a ray that will be transmitted through the prism is
A30∘B45∘C15∘D50∘A ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2 , the angle of incidence on the first face of the prism is
A30∘B45∘C60∘D0∘
A ray of light is incident on a prism of refracting angle A. if θC is the critical angle for the material of the prism with respect to the surrounding air, then:
View SolutionA monochromatic light is incident at a certain angle on an equilateral triamgular prism and suffers minimum deviation . If the refractive index of the material of the prism is √3, them the angle of incidence is :
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes through the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2, the angle of incidence on the first face of the prism is
View SolutionA ray of monochromatic light is incident on one refracting face of a prism of angle 75∘. It passes thorugh the prism and is incident on the other face at the critical angle. If the refractive index of the material of the prism is √2, the angle of incidence on the first face of the prism is
View SolutionWhen light rays are incident on a prism at an angle of 45∘, the minimum deviation is obtained. If refractive index of the material of prism is √2, then the angle of prism will be
View Solution
