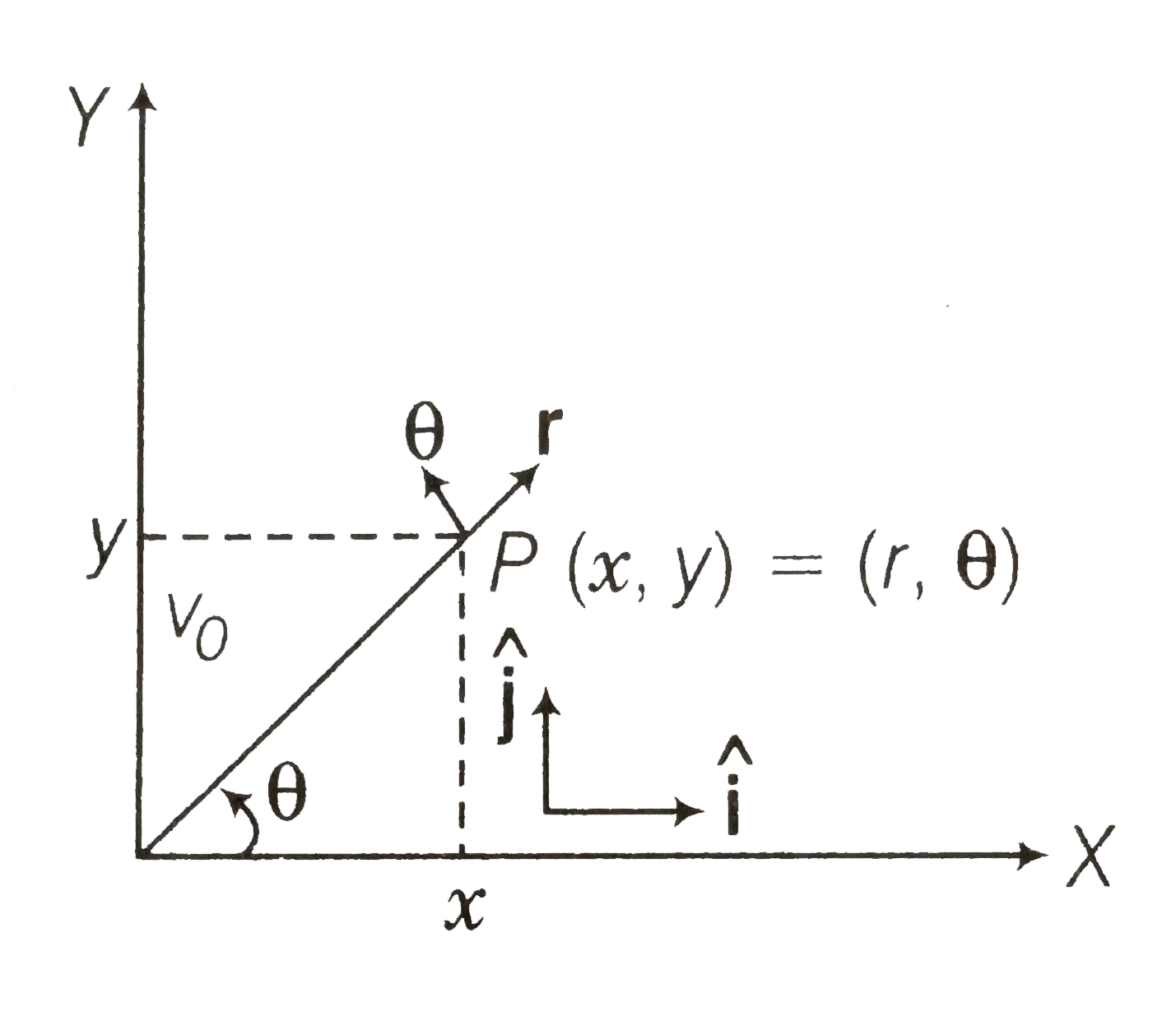
Motion in two dimensions, in a plane can be studied by expressing position, velocity and acceleration as vectors in cartesian coordinates $A = A_{x} ˆ i + A_{y} ˆ j$ , where $ˆ i$ and $ˆ j$ are unit vector along x and y-directions, respectively and $A_{x}$ and $A_{y}$ are corresponding components of A. Motion can also be studied by expressing vectors in circular polar coordinates as $A = A_{r} ˆ r + A_{θ} ˆ θ$ , where $ˆ r = \frac{r}{r} = cos θ ˆ i + sin θ ˆ j$ and $ˆ θ = - sin θ ˆ i + cos θ ˆ j$ are unit vectors along direction in which r and $θ$ are increasing.
(a) Express $ˆ i$ and $ˆ j$ in terms of $ˆ r$ and $ˆ θ$ .
(b) Show that both $ˆ r$ and $ˆ θ$ are unit vectors and are perpendicular to each other.
(c) Show that $\frac{d}{d t} (ˆ r) = ω ˆ θ$ , where $ω = \frac{d θ}{d t}$ and $\frac{d}{d t} (ˆ θ) = - θ ˆ r$ .
(d) For a particle moving along a spiral given by $r = a θ ˆ r$ , where a = 1 (unit), find dimensions of a .
(e) Find velocity and acceleration in polar vector representation for particle moving along spiral described in (d) above.

Video Solution

Text Solution

Verified by Experts

(a) $ˆ r = cos θ + sin θ j ˆ j$
$ˆ θ = - sin θ ˆ I + cos a θ ˆ j$ ….(i)
Multipluing (i) by $sin θ$ and (ii) with $cos θ$ and adding, we get ….(ii)
$ˆ e = - sin θ + ˆ θ cos h t η = ({sin}^{2} θ + {cos}^{\circ} θ) ˆ j = ˆ j$ or hat r sin theta + hat theta cos theta = hat j $... . (i i i) M j t - i p l y \in g (i) b y cos θ and (i i) b y sin θ and \subset t r a c t \in g, w e \geq t$ ltbr> ( hat r cos theta - hat theta sin theta ) = hat i $... . (i v) (b)$ hat i. hat theta = ( hat i + sin theta hat j). (- sin theta hat i + cos theta hat j) $ (1) (1)$ cos theta =- cos theta sin theta + sin theat cos theta =0= cos 90^@ $or$ theta = 90^@ $ (c) \frac{d}{d r} ˆ r) = \frac{d}{d r} cos θ {ˆ i}_{+} sin θ ˆ j) = - sin θ \frac{d θ}{d t} ˆ i cos t e h t a \frac{d θ}{d t} ˆ i + cos θ \frac{d t h η}{d t} ˆ j = ω [- sin ˆ i + cos θ ˆ j] = ω ˆ i θ$ ltBrgt (d) $\to r = α θ ˆ r$ or $| \to r | = α θ$ or alpha = (|vec r|)/(theta) $ D i m e n s i o n s o f$ alpha L/1 = L = [M^0 L^1 T^0 ] $ (E) G i v e n,$ alpha =1 $u n i t, o m a b o v e, w e h a v e$ vec r = theta hat r = theta [ cos theta hat i + sin theta hat j] $ v e l o c i t y,$ vec r = (d vec r)/(dt) = ( d theta )/( dt) vec r + theta [ - sin theta hat i + cos theta hat j] ( d theta)/(dt) vec r + theta hat i theta omega $[∴ \frac{d θ}{d t} = m o e g a]$
$ω ˆ r + ω ˆ θ$
Accelration, $\to a = \frac{d}{d t} [ω θ ˆ θ] = \frac{d}{d t} [\frac{d θ}{d t} \times (θ ˆ θ)] = \frac{d^{2} θ}{{d t}^{2}} ˆ r + \frac{d θ}{d t} \frac{d ˆ r}{d t} + \frac{d^{2} θ}{{d t}^{2}} \times \frac{d θ}{d t} \frac{d}{d t} (θ ˆ θ)$
$= \frac{d^{2} θ}{s t^{\circ}} ˆ r + ω \frac{d}{d t} [cos θ ˆ i + sin θ ˆ j] + (d^{2} θ) \frac{.}{{d t}^{2}} θ ˆ θ + ω \frac{d}{d t} (θ ˆ θ)$
$= \frac{d^{2} t h e a}{{d t}^{2}} ˆ r ω [- sin h η ˆ i + c i s θ ˆ j] \frac{d θ}{d t} + \frac{d^{2} θ}{{d t}^{2}} θ ˆ θ + ω [\frac{d t e h t a}{d t} ˆ θ + θ) d ˆ θ \frac{)}{d t}]$
$= \frac{d^{2} θ}{{d t}^{2}} ˆ r + ω 2 ˆ θ + \frac{d^{2} θ}{{d t}^{2}} \times θ ˆ θ + ω^{2} ˆ θ + ω^{2} θ (- ˆ e)$ $[∴ \frac{d ˆ θ}{d t} = - ω ˆ r]$
$= \frac{d^{2} θ}{{d t}^{2}} - ω^{2} θ) ˆ r + (2 ω^{2} + \frac{d^{2} θ}{{d t}^{2}} θ) ˆ θ$ .

Updated on:21/07/2023

The angle which the vector $\to A = 2 ˆ i + 3 ˆ j$ makes with the y-axis, where $ˆ i$ and $ˆ j$ are unit vectors along x- and y-axis, respectively, is
A ${cos}^{- 1} (3 / 5)$
B ${cos}^{- 1} (2 / 3)$
Ctan^(-1)(2//3)
D ${sin}^{- 1} (2 / 3)$
The unit vector along $ˆ i + ˆ j$ is
A $ˆ k$
B $ˆ i + ˆ j$
C $\frac{ˆ i + ˆ j}{\sqrt{2}}$
D $\frac{ˆ i + ˆ j}{2}$
If $ˆ i, ˆ j, ˆ k$ are the unit vectors and mutually perpendicular, then $[\begin{matrix} ˆ i & ˆ j & ˆ k \end{matrix}]$ =
A $0$
B $- 1$
C $1$
D $2$