Question

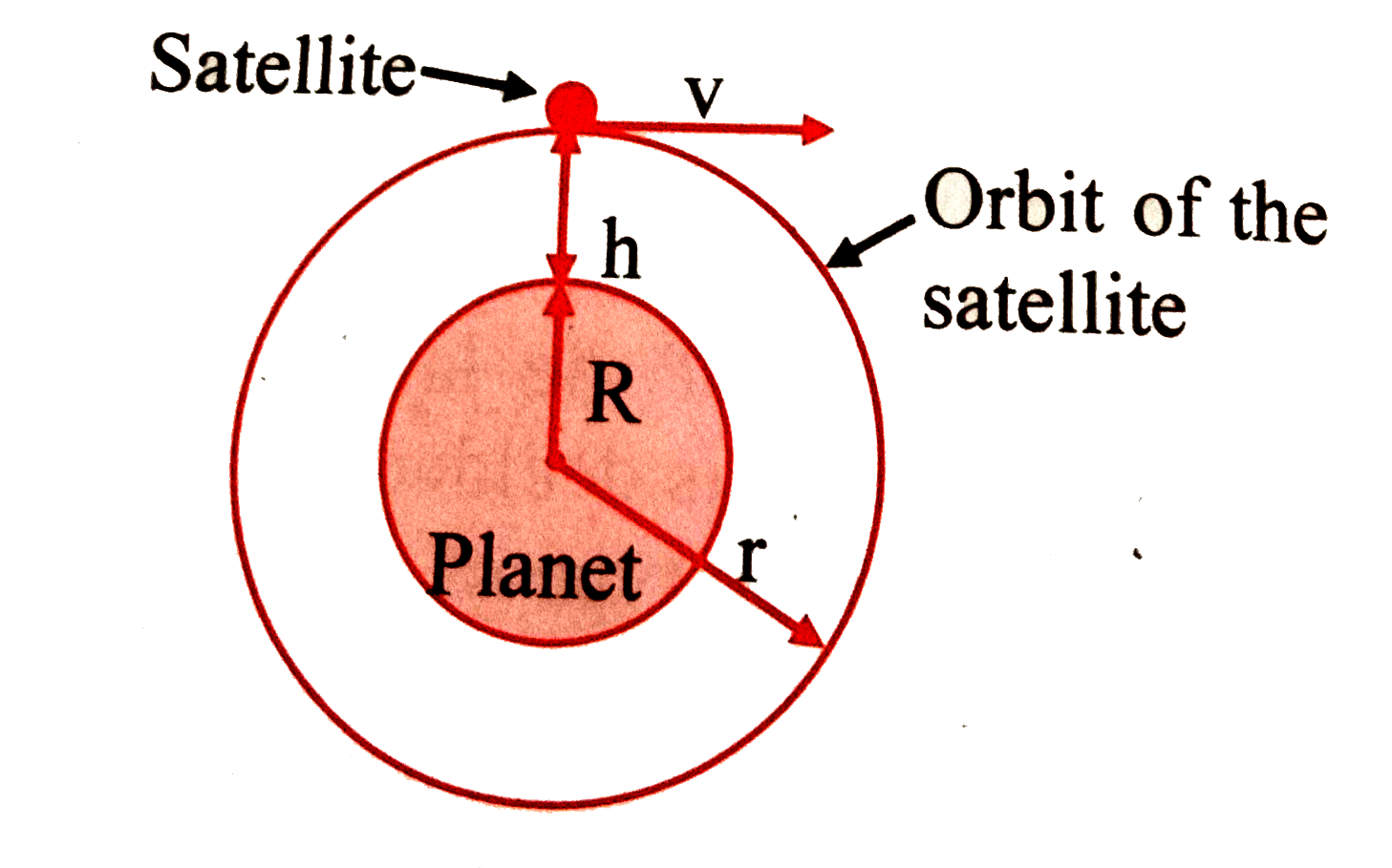
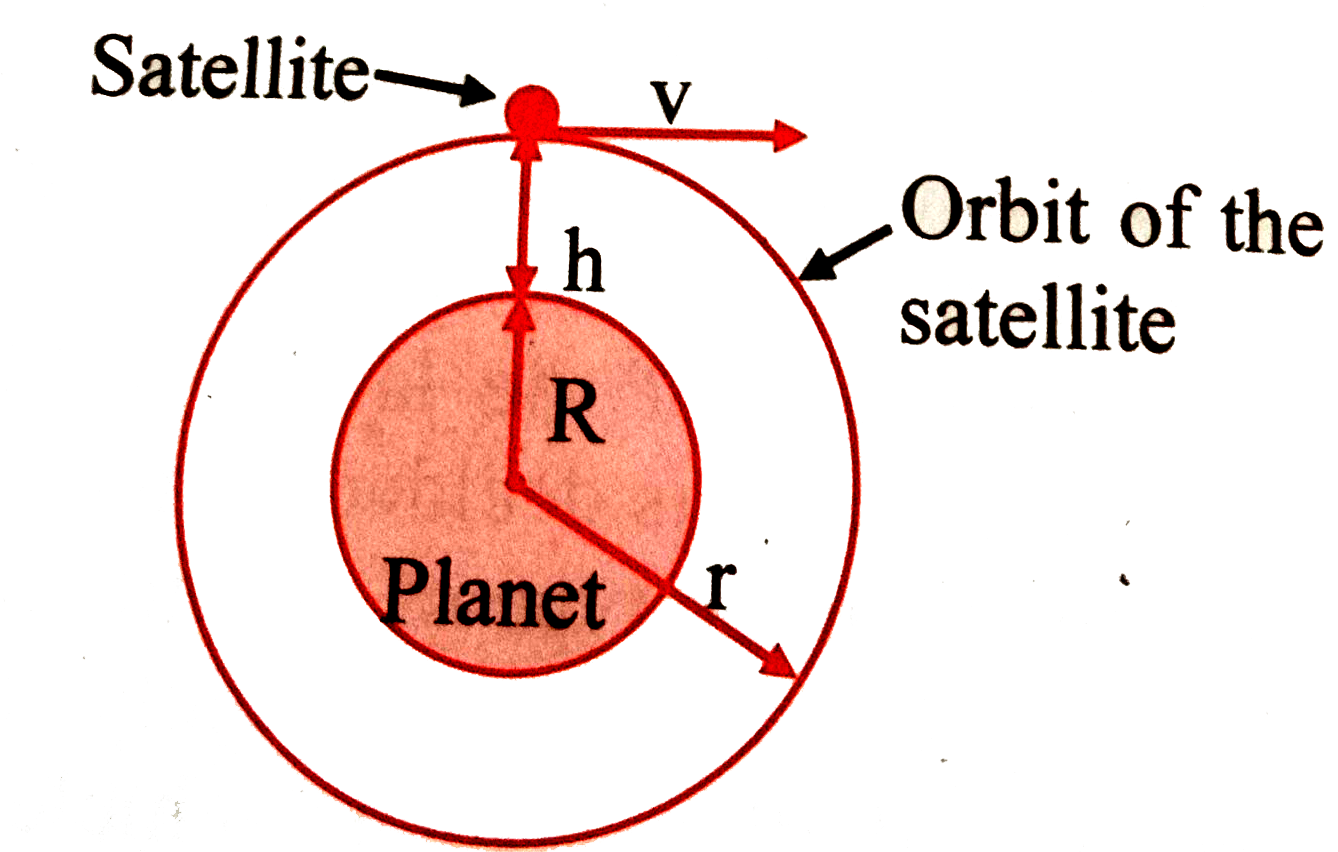
Observe the following diagram and answer the questions:

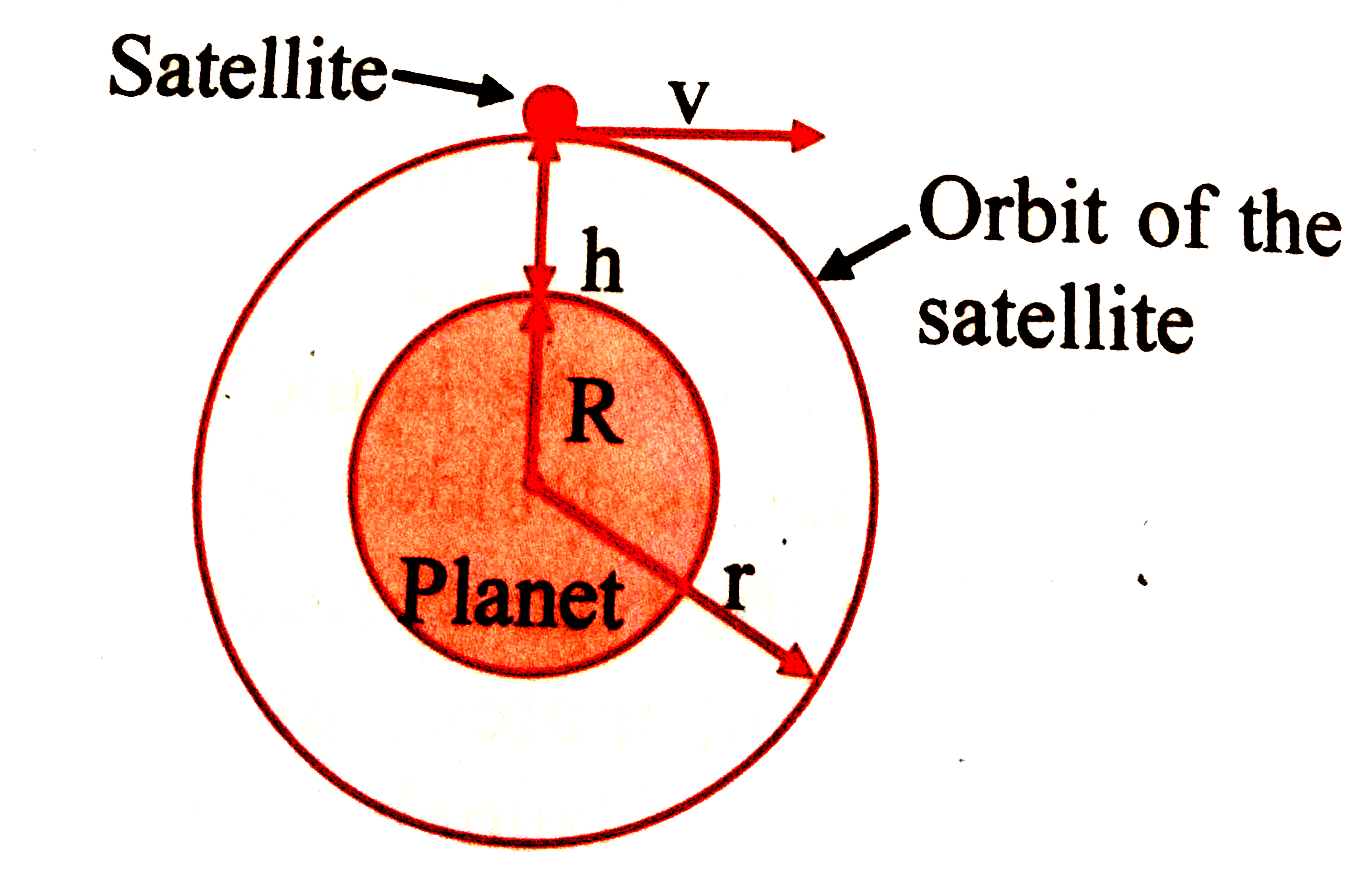
Derive the formula for that velocity of satellite assuming the mass of the planet M and mass of satellite as m .

Explanation

Critical velocity of a satellite revolving around the planet in circular orbit can be derived as follows: Consider the satellite of mass m revolving at height around the planet of mass M and radius above . As the satellite is moving in circular orbit, centripetal force acting on it is provided by the gravitational force of the planet,
i e . , `(mv^(2))/(r)=(GMm)/(r^(2))`
But r =R+h
`therefore" " v^(2)=(GM)/((R+h))`
`therefore" " v=sqrt((GM)/(R+h))`
Hence , critical velocity is given by formula
`sqrt((GM)/(R+h))`.