On a winter day when the atmospheric temperature drops to −10∘C, ice form on the surface of a lake.
(a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed.
(b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches 0∘C before the ice starts froming. Density of water =1000kg/m3, latent heat of fusion of ice =3.36×105J/kg and thermal conductivity of ice =1.7W/m−∘C. Neglect the expansion of water on freezing
(a) Let a time t, thickness of ice formed is x
Let in time dt, thickness of ice formed is dx.
Rate of heat flow through ice
dQdt=KA[0−(−θ)]x
Let in time dt, mass of ice formed is dm
dQ=dmL=ρAdxL
From (i) and (ii)
ρAdxLdt=KAθx
dxdt=KθρLx=1.7×101000×3.36×105×0.1=5×10−7m/s
(b) ∫dt=ρL2Kθ∫x0xdx
t=ρLx22Kθ=1000×3.36×105×(0.1)22×1.7×10
=976605=2.71hr

Topper's Solved these Questions
Similar Questions
On a winter day when the atmospheric temperature drops to −10∘C , ice forms on the surface of a lajke. (a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed. (b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches 0∘C before the ice starts forming. Density of water =1000kgm−3 , latent heat of fusion of ice =3.36×105Jkg−1 and thermal conductivity of ice =1.7Wm−1^(@)C^(-1) . Neglect the expension of water on freezing.
View SolutionOn a winter day when the atmospheric temperature drops to −10∘C , ice forms on the surface of a lake. (a) Calculate the rate of increases of thickness of the ice when 10cm of ice is already formed. (b) Calculate the total time taken in forming 10cm of ice. Assume that the temperature of the entire water reaches 0∘C before the ice starts forming. Density of water =1000kgm−3 , latent heat of fusion of ice =3.36×105Jkg−1 and thermal conductivity of ice =1.7Wm−1C−1 . Neglect the expansion of water on freezing.
View Solution
Knowledge Check
The atmospheric temperature in the surroundings of a lake is -10 °C while the water in the lake is at 0 °C. If it takes 7 h to form 1 cm thick ice, then how much time is required to form another 1 cm of ice ?
A7hB14hCLess than 7hDMore than 7hOn a cold winter dry, the temperature of atmosphere is −T∘C. The cylindrical dram shown is made of insultating material and it contains water at 0∘C. If L is latent heat of fusion of ice, ρ is density of ice and KR is thermal conductivity of ice, the time taken for total mass of water to freeze is
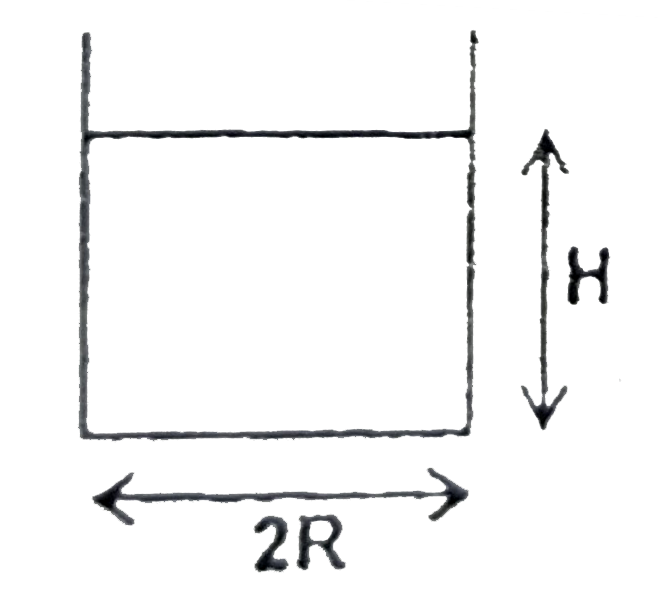 AρLH2KTBρLH22KTCρLH2KTDH2ρLKT
AρLH2KTBρLH22KTCρLH2KTDH2ρLKTWhen water at 0∘C freezes to form ice at the same temperature of 0∘C, then it :
Aabsorbs some heatBreleases some heatCneither absorbs nor releases heatDabsorbs exactly 3.34×105J/kg of heat
A piece of ice of mass 40 g is dropped into 200 g of water at 50∘C. Calculate the final temperature of water after all the ice has melted (sp. heat capacity of water =4200J/kg∘C, sp. latent heat of fusion of ice = 336×103J/kg)
View SolutionBottom of a lake is at 0∘C and atmospheric temperature is −20∘C. If 1 cm ice is formed on the surface in 24 h, then time taken to form next 1 cm of ice is
View SolutionBottom of a lake is at 0∘C and atmospheric temperature is −20∘C. If 1 cm ice is formed on the surface in 24 h, then time taken to form next 1 cm of ice is
View SolutionA: The rate of growth of ice on the surface of a lake decreases with increase in thickness of Ice layer.
R: Ice is poor conductor of heat energy.
View SolutionOn a cold winter dry, the temperature of atmosphere is −T∘C. The cylindrical dram shown is made of insultating material and it contains water at 0∘C. If L is latent heat of fusion of ice, ρ is density of ice and KR is thermal conductivity of ice, the time taken for total mass of water to freeze is

View Solution
