On an inclined plane two particles AandB are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of AandB is cotθ, where θ is the angle at which B is projected measured from inclined plane, find the angle at which particles are projected.
30∘
45∘
15∘
60∘
The correct Answer is:B
Time of flights of AandB
TA=2usin(∝+β)gcosβ and
TB=2usin(∝−β)gcosβ
TATB=sin(∝+β)sin(∝−β)=cotθ (given)
⇒cosθsinθ=sin(90−θ)sinθ=sin(∝+β)sin(∝−β)
We can write, ∝+β=90−θ ...(i)
and ∝−β=θ ...(ii)
on solving (i) and (ii) we get, ∝=45∘.
 .
.
Topper's Solved these Questions
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.3
12 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.4
11 Videos
- KINEMATICS-2BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-2EXERCISE - Exercise 5.1
15 Videos
- KINEMATICS-1BOOK - CENGAGE PHYSICSCHAPTER - KINEMATICS-1EXERCISE - Integer
9 Videos
- KINETIC THEORY OF GASESBOOK - CENGAGE PHYSICSCHAPTER - KINETIC THEORY OF GASESEXERCISE - Compression
2 Videos
Similar Questions
A particle of mass m is projected with a speed u at an angle θ with the horizontal. Find angular momentum of particle after time t about point of projection.
View SolutionA particle is projected with a speed v at an angle θ with the horizontal. Find the mean power delivered by gravity during the ascent of the particle.
View Solution
Knowledge Check
On an incliend plane two particles A and B are projected with same speed at the same angle with the horizontal, particle A down and particle B up the plane. If the ratio of time of flight of A and B is cot θ, is the angle at which B is projected measured from. inclined plane, find the angle at which particles are projected.
A90∘B60∘C30∘D45∘From an inclined palne two particles P,Q are projected with same speed at same angle θ,one up and other down the plane as shown in figure.Which of the following statement(s) is/are correct ?
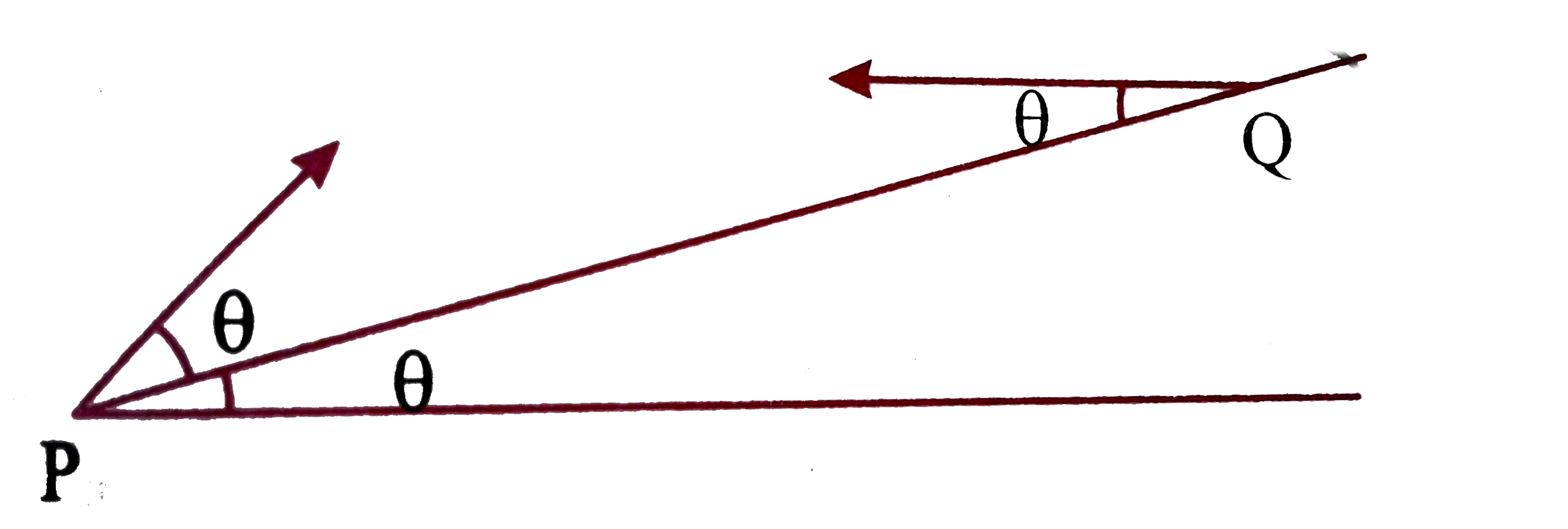 AThe particles will collide the plane with same speedBThe times of flight of each particle are sameCBoth particles strike the plane perpendicularlyDThe particles will collide in mid air if projected simultaneuosly and time of flight of each particle is less than the time of collision.
AThe particles will collide the plane with same speedBThe times of flight of each particle are sameCBoth particles strike the plane perpendicularlyDThe particles will collide in mid air if projected simultaneuosly and time of flight of each particle is less than the time of collision.A particle is projected with a speed u at an angle θ with the horizontal. What will be the speed of the particle when direction of motion of particle is at an angle α with the horizontal?
AucosθsecαBusecθcosαCucosθtanαDucosθcotα
Two particles are projected with same velocity but at angles of projection 35 and 55 then their horizontal ranges are in the ratio of
View Solution" Two particles are projected with same velocity but at angles of projection 35∘ and 55∘.Then their horizontal ranges are in the ratio
View SolutionTwo particles are projected with same speed but at angles of projection (45∘−θ) and (45∘+θ). Then their horizontal ranges are in the ratio of
View SolutionA particle is projected with velocity v at an angle θ aith horizontal. The average angle velocity of the particle from the point of projection to impact equals
View SolutionTwo bodies AandB are projected from the same place in same vertical plane with velocities v1andv2.Form a long inclined plane as shown Find the ratio of their times of flight.
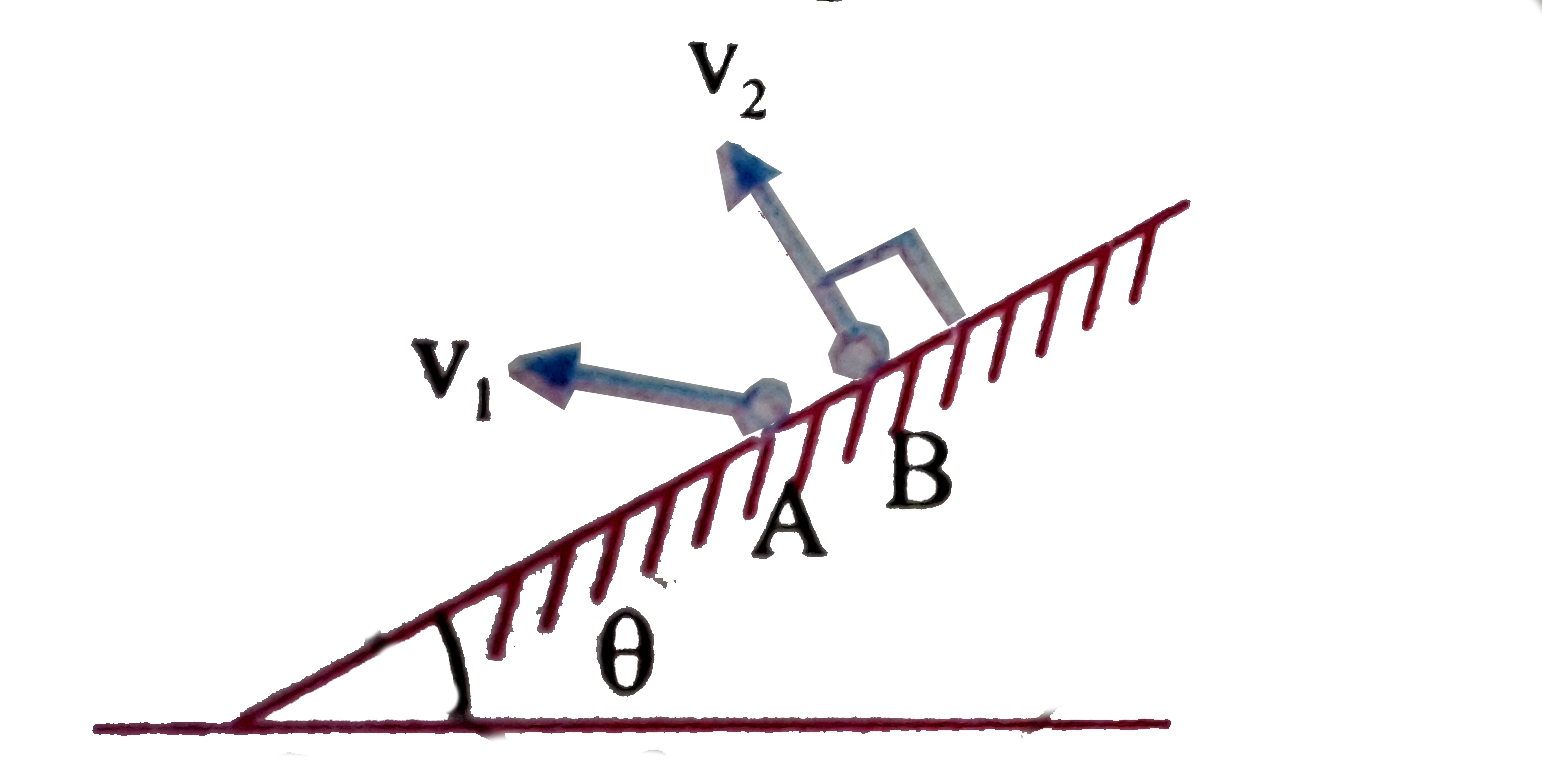
View Solution
