On increasing the length by 0.5 mm in a steel wire of length 2 m and area of cross section 2mm2, the force required is [Y for steel =2.2×1011Nm2]
1.1×105N
1.1×104N
1.1×103N
1.1×102N
The correct Answer is:D
To find the force required to increase the length of a steel wire by 0.5 mm, we can use the formula for Young's modulus (Y):
Y=StressStrain
Where:
- Stress = FA (Force per unit area)
- Strain = ΔLL0 (Change in length per original length)
Given:
- Original length, L0=2m
- Change in length, ΔL=0.5mm=0.5×10−3m
- Area of cross-section, A=2mm2=2×10−6m2
- Young's modulus for steel, Y=2.2×1011N/m2
Step 1: Calculate Strain
Strain is calculated as:
Strain=ΔLL0=0.5×10−3m2m=0.25×10−3
Step 2: Rearranging Young's Modulus Formula
From the Young's modulus formula, we can rearrange to find the force F:
Y=F/AΔL/L0⟹F=Y⋅Strain⋅A
Step 3: Substitute Values
Now substitute the values into the equation:
F=2.2×1011N/m2⋅(0.25×10−3)⋅(2×10−6m2)
Step 4: Calculate the Force
Calculating the force:
F=2.2×1011⋅0.25×10−3⋅2×10−6
F=2.2×0.25×2×1011−3−6
F=1.1×102N
F=110N
Final Answer
The force required to increase the length of the steel wire by 0.5 mm is 110 N.
---
- Stress = FA (Force per unit area)
- Strain = ΔLL0 (Change in length per original length)
- Original length, L0=2m
- Change in length, ΔL=0.5mm=0.5×10−3m
- Area of cross-section, A=2mm2=2×10−6m2
- Young's modulus for steel, Y=2.2×1011N/m2
Strain is calculated as:
Strain=ΔLL0=0.5×10−3m2m=0.25×10−3
From the Young's modulus formula, we can rearrange to find the force F:
Y=F/AΔL/L0⟹F=Y⋅Strain⋅A
Now substitute the values into the equation:
F=2.2×1011N/m2⋅(0.25×10−3)⋅(2×10−6m2)
Calculating the force:
F=2.2×1011⋅0.25×10−3⋅2×10−6
F=2.2×0.25×2×1011−3−6
F=1.1×102N
F=110N
The force required to increase the length of the steel wire by 0.5 mm is 110 N.
Topper's Solved these Questions
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Bulk Modulus And Shear Modulus29videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - PROPERTIES OF MATTEREXERCISE - Elasticity And Work Done In Stretching A Wire25videos
PROPERTIES OF MATTER
- BOOK - A2ZCHAPTER - OSCILLATION AND SIMPLE HARMONIC MOTIONEXERCISE - Chapter Test29videos
OSCILLATION AND SIMPLE HARMONIC MOTION
- BOOK - A2ZCHAPTER - ROTATIONAL DYNAMICSEXERCISE - Chapter Test29videos
ROTATIONAL DYNAMICS
Similar Questions
Assertion : To increase the length of a thin steel wire of 0.1cm2 corss sectional area by 0.1%, a force of 2000 N is required, its Y=200×109Nm−2.
Reson : It is calculated by Y=F/LA×ΔLView SolutionCalculate the force required to increase the length of a steel wire of cross- sectional area 10−6m2 by 0.5% given: Y(for steel)=2×1011N−m2
View Solution
Knowledge Check
- Question 1 - Select One
For increasing the length by 0.5mm in a steel wire of length 4m and area of cross section 5mm2, the force required is (Y=11.90×1012N/m2)
A4×107NB2×103NC7.4×103ND103N - Question 2 - Select One
A steel wire of length 2.5 m and area of cross section 1.25mm2, when it is stretched by a force of 40 N and Y for steel is 2×1011N/m2. The extension produced in a steel wire is
A0.4 mmB0.4 cmC4 mmD4 cm - Question 3 - Select One
A steel wire of length 5 m and area of cross-section 4mm2 is stretched by 2 mm by the application of a force. If young's modulus of steel is 2×1011N/m2, then the energy stored in the wire is
A0.64 JB0.16 JC0.32 JD1.28 J
Compute the elongation of the steel wire and brass wire in the given
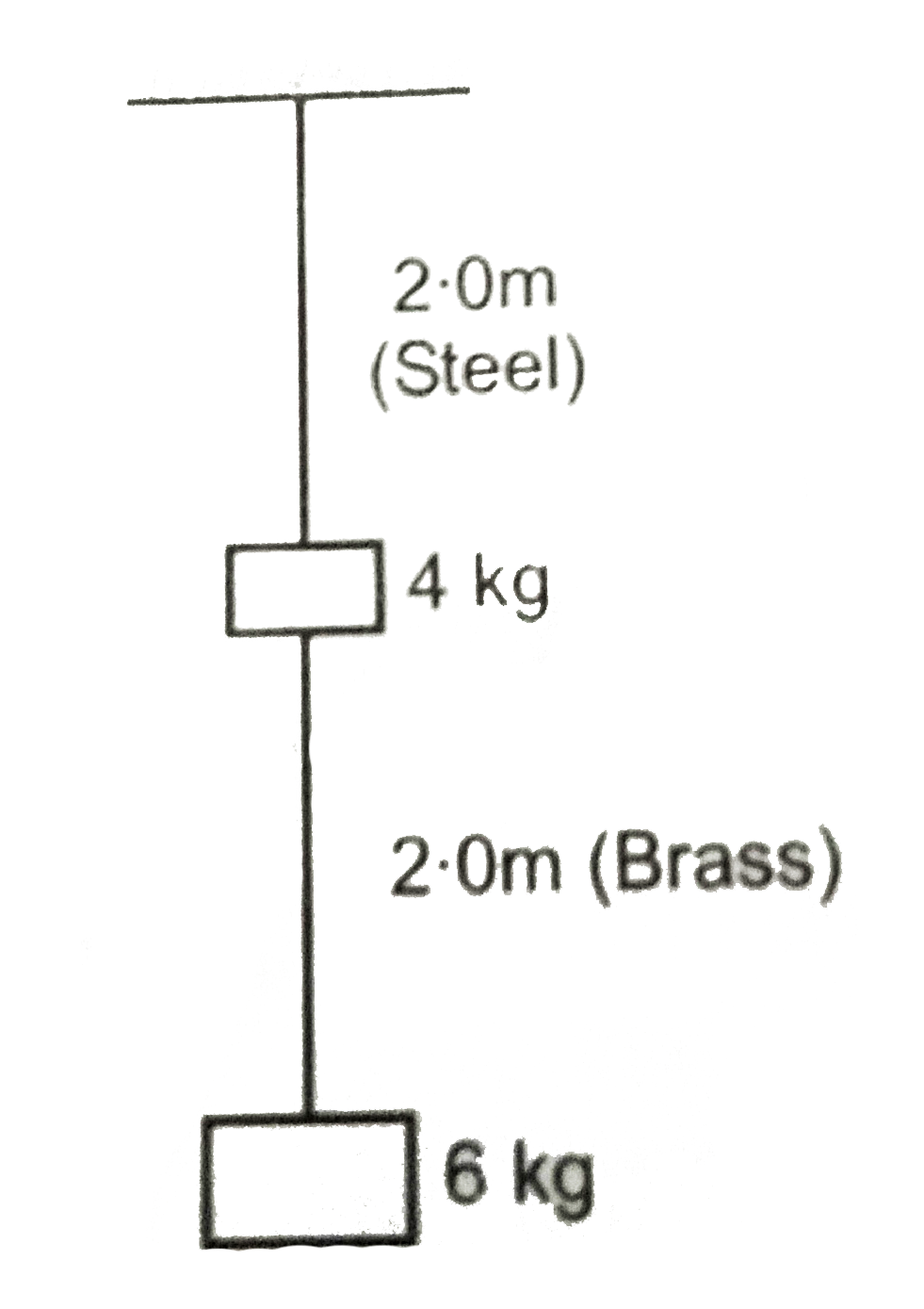
Given unloaded length of steel wire = 2.0 m, unloaded length of brass wire = 1.0m. Area of cross-section of each wire =0.049cm2.
Ysteel=2×1011Pa
and YBrass=0.90×1011Pa,g=9.8ms−2View SolutionA wire of length 50cm and cross sectional area of 1 sq. mm is extended by 1mm. The required work will be (Y=2×1010Nm−2)
View SolutionIn an experiment, brass and steel wires of length 1 m each with areas of cross section 1mm2 are used. The wires are connected in series and one end of the combined wire is connected to a rigid support and other end is subjected to elongation. The stress required to produce a net elongation of 0.2 mm is, [Given, the Young’s Modulus for steel and brass are, respectively, 120×109N/m2and60×109N/m2
View SolutionTo double the length of a iron wire having 0.5cm2 area of cross-section, the required force will be (Y=1012dyne/cm2)
View SolutionWhen a wire is stretched, an amount of work is done. What is the amount of work done in stretching a wire through 0.1 mm, if its lengths is 2m and area of cross-section 10−6m2(Y=2×1011N/m2)
View Solution

