One end of a horizontal thick copper wire of length 2L and radius 2R is welded to an end fo another horizontal thin copper wire of lenth L and radius R. When the arrangement is stretched by applying forces at two ends, the ratio of the elongation in the thin wire to that in the thick wire is
0.25
 0.50
 2.00
4.00
The correct Answer is:C
To solve the problem, we need to find the ratio of the elongation in the thin wire to that in the thick wire when both are subjected to the same force. We will use the concept of Young's modulus, which relates stress and strain in materials.
1. Understanding Young's Modulus:
Young's modulus (Y) is defined as:
Y=StressStrain=F/AΔL/L
where:
- F = force applied,
- A = cross-sectional area,
- ΔL = change in length (elongation),
- L = original length.
2. Cross-Sectional Areas:
- For the thick wire (length = 2L, radius = 2R):
Athick=π(2R)2=4πR2
- For the thin wire (length = L, radius = R):
Athin=πR2
3. Applying Young's Modulus for Each Wire:
- For the thick wire:
Y=FAthick⋅LΔL1⟹Y=F4πR2⋅2LΔL1
- For the thin wire:
Y=FAthin⋅LΔL2⟹Y=FπR2⋅LΔL2
4. Equating Young's Modulus:
Since both wires are made of the same material (copper), their Young's moduli are equal:
F⋅2L4πR2⋅ΔL1=F⋅LπR2⋅ΔL2
5. Canceling Common Terms:
We can cancel F and πR2 from both sides:
2L4ΔL1=LΔL2
6. Rearranging the Equation:
Rearranging gives:
ΔL2=L⋅4ΔL12L=2ΔL1
7. Finding the Ratio of Elongations:
The ratio of elongation in the thin wire to that in the thick wire is:
ΔL2ΔL1=2
Final Answer:
The ratio of the elongation in the thin wire to that in the thick wire is 2.
---
Young's modulus (Y) is defined as:
Y=StressStrain=F/AΔL/L
where:
- F = force applied,
- A = cross-sectional area,
- ΔL = change in length (elongation),
- L = original length.
- For the thick wire (length = 2L, radius = 2R):
Athick=π(2R)2=4πR2
- For the thin wire (length = L, radius = R):
Athin=πR2
- For the thick wire:
Y=FAthick⋅LΔL1⟹Y=F4πR2⋅2LΔL1
- For the thin wire:
Y=FAthin⋅LΔL2⟹Y=FπR2⋅LΔL2
Since both wires are made of the same material (copper), their Young's moduli are equal:
F⋅2L4πR2⋅ΔL1=F⋅LπR2⋅ΔL2
We can cancel F and πR2 from both sides:
2L4ΔL1=LΔL2
Rearranging gives:
ΔL2=L⋅4ΔL12L=2ΔL1
The ratio of elongation in the thin wire to that in the thick wire is:
ΔL2ΔL1=2
The ratio of the elongation in the thin wire to that in the thick wire is 2.
Topper's Solved these Questions
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - NCERT
8 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - CORNER
15 Videos
- MECHANICAL PROPERTIES OF SOLIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF SOLIDSEXERCISE - APPLICATIONS OF ELASTIC BEHAVIOUR OF MATERIALS
8 Videos
- MECHANICAL PROPERTIES OF FLUIDSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - MECHANICAL PROPERTIES OF FLUIDSEXERCISE - NCERT Exemplar
5 Videos
- MOTION IN A PLANE BOOK - NCERT FINGERTPS ENGLISHCHAPTER - MOTION IN A PLANE EXERCISE - Assertion And Reason
15 Videos
Similar Questions
One end of a horizontal thick copper wire of length 2L and radius 2R is weded to an end of another horizontal thin copper wire of length L and radius R .When the arrangement is stretched by applying forces at two ends , the ratio of the elongation in the thin wire to that in the thick wire is
View SolutionTwo wires of the same material and length are stretched by the same force. Their masses are in the ratio 3:2. Their elongations are in the ratio
View Solution
Knowledge Check
A wire of length L and radius r is clamped at one end. On stretching the other end of the wire with a force F, the increase in its length is 1. If another wire of same material but of length 2L and radius 2r is stretched with a force 2F, the increase in its leagth will be
Al4Bl2ClD2l
Two wires of the same material and same mass are stretched by the same force. Their lengths are in the ratio 2:3. Their elongation are in the ratio
View SolutionA force F is required to break a wire of length L and radius r. Find the force required to break a wire of the same material, length 2L and radius 4r.
View SolutionOne end of a Nichrome wire of length 2L and cross-sectional area A is attached to an end of another Nichrome wire of length L and cross-sectional area 2A. If the free end of the longer wire is at an electric potential of 8.0 volts, and the free end of the shorter wire is at an electric potential 1.0 volts, the potential at the junction of the two wires is equal to
View SolutionA wire of length l has a resistance R. If half of the length is stretched to make the radius half of its original value, then the final resistance of the wire is
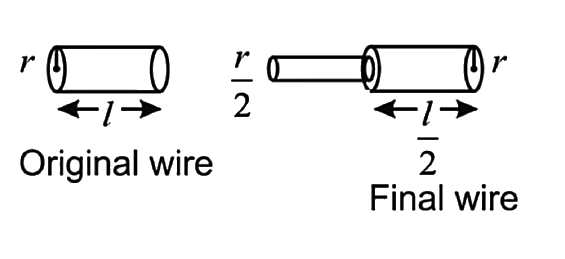
View SolutionA force F is needed to break a copper wire having radius R. The force needed to break a copper wire of same length and radius 2R will be
View SolutionTwo wires of copper having the length in the ratio 2:1 and their radii ratio as 1:2 are stretched by the same force. The ratio of longitudinal strain in the two will be
View SolutionTwo wires of the same length and same material but radii in the ratio of 1:2 are stretched by unequal forces to produce equal elongation. The ratio of the two forces is
View Solution
