One end of a light spring constant and natural length is fixed and the other end is attached to a block of mass lying on smooth horizontal surface. If the block is rotating in the horizontal circle of radius , find the frequency of the revolution.
Extension of spring
Here, the necessary centripetal force is provide by the spring force
where is the frequency of revolution.

Topper's Solved these Questions
Similar Questions
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacement, the work by the spring is 12kx2. The possible cases are
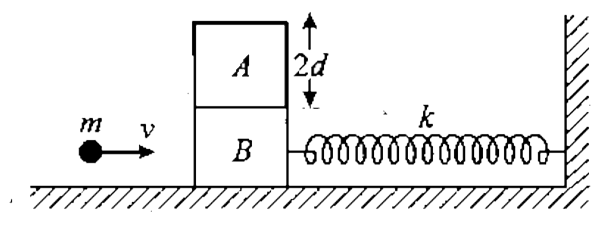
View SolutionA and B are two identical blocks of same mass 2 m and same physical dimensions as shown in figure −4.158 A is placed over the block B which is attached to one end of the spring of natural length l and spring contant k. The other end of the speing is attached to a wall. The system is resting on a smooth horizontal surface with the spring in the relaxed state. A small object of mass m moving horizontally with speed v at a height d above the horizontal surface hits the block B along the line of therir cntre of mass in a perfectly elastic collision. There is no friction between A and B.
Find the minimum value of v (sayvo)such that the block A will topple over block B.
What is the energy stored in the spring when the blocks A and B returns to their initial position as before collision
View Solution
Knowledge Check
One end of a light spring of spring constant k is fixed to a wall and the other end is tied to a block placed on a smooth horizontal surface. In a displacment, the work done by the spring is +(12)kx2. The possible cases are.
AThe spring was initially compessed by a distance x and was finally in its natural length .BIt was initially stretched by a distance x and finally was in its natural length.CIt was initially natural length and finally in a compressed position.DIt was initially in its natural length and finally in a stretched position.Two blocks each of mass m are joined together using an ideal spring of force constant K and natural length l0 . The blocks are touching each other when the system is released from rest on a rough horizontal surface. Both the blocks come to rest simultaneously when the extension in the spring is l04. The coefficient of friction between each block and the surface (assuming it to be same between any of the blocks and the surface) is :
AKl040mgBKl08mgC3Kl08mgD1720Kl0mgOne end of a spring of force constant k is fixed to a vertical wall and the other to a block of mass m resting on a smooth horizontal surface There is another and wall at a distance x0 from the block The spring is then compressed by 2x0 and released The time taken to at the wall is
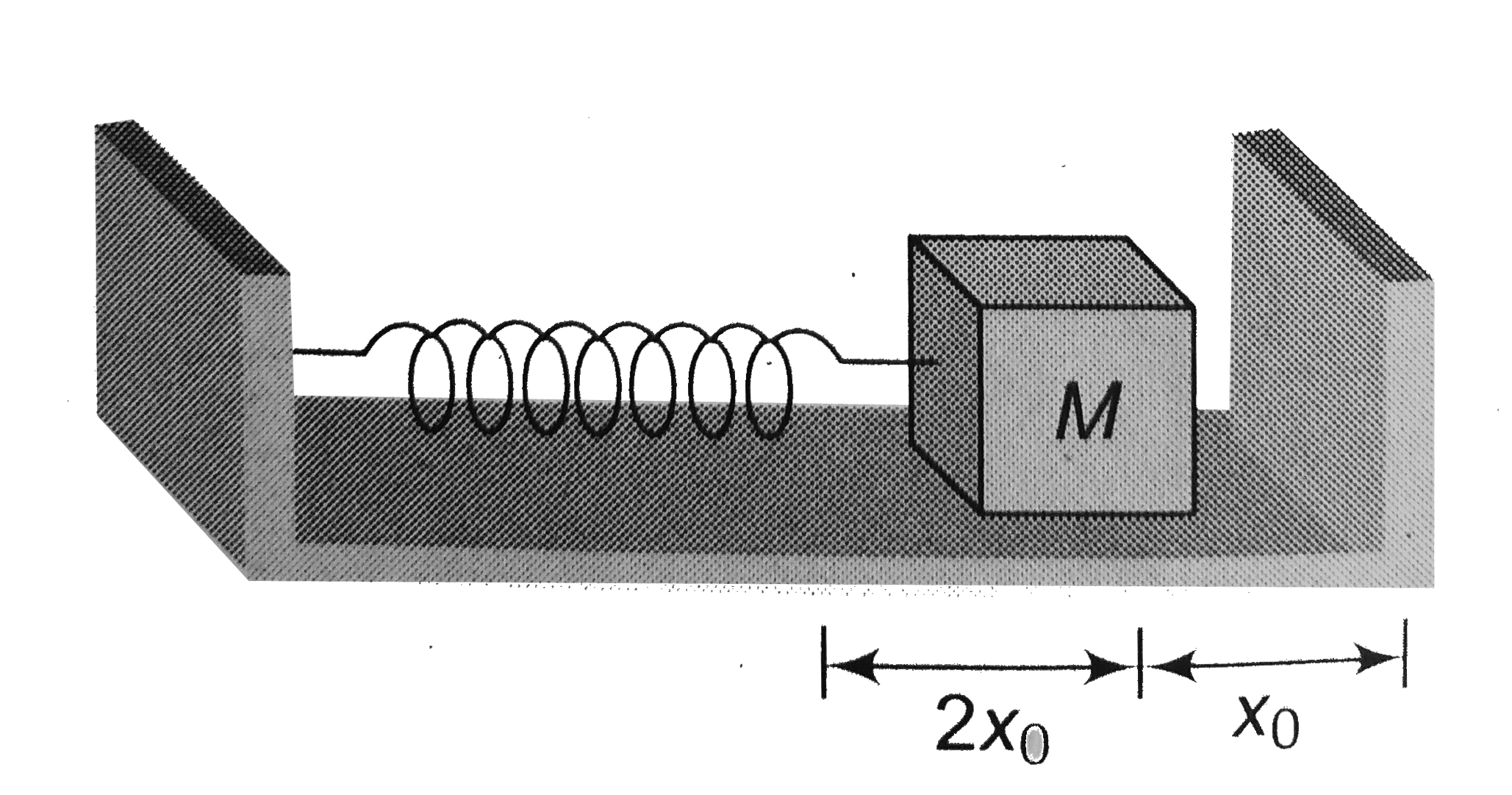 A16π√kmB√kmC2π3√mkDπ4√km
A16π√kmB√kmC2π3√mkDπ4√km

A ring of mass m is attached to a horizontal spring of spring constant k and natural length l0. The other end of the spring is fixed and the ring can slide on a horizontal rod as shown. Now the ring is shifted to position B and released Find the speed of the ring when the spring attains its natural length.
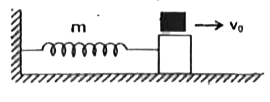
View SolutionA spring of mass m lies on a smooth table. One, end of it is clamped to the vertical wall and other end is attached to a mass m ( as shown in fig) and is placed on a horizontal frictionless surface. If the block of mass M is given a velocity v0 towards right find the K.E. of the system . ( AsSigmae velocity in spring is varying linearly).
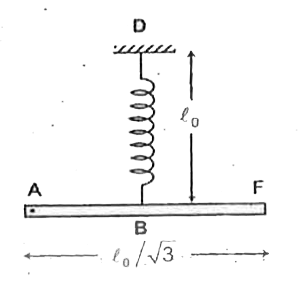
View SolutionIn the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
View SolutionA rotor is rotating with a constant angular velocity ω about its own axis. At the centre of the rotaor a spring is fixed of natural length (l0) whose other end is connected to a block of mass m. Find the minimum vaule of coefficient of friction between block and rotor wall for which spring remains horizontal. The radius of rotor is R(R<l0).
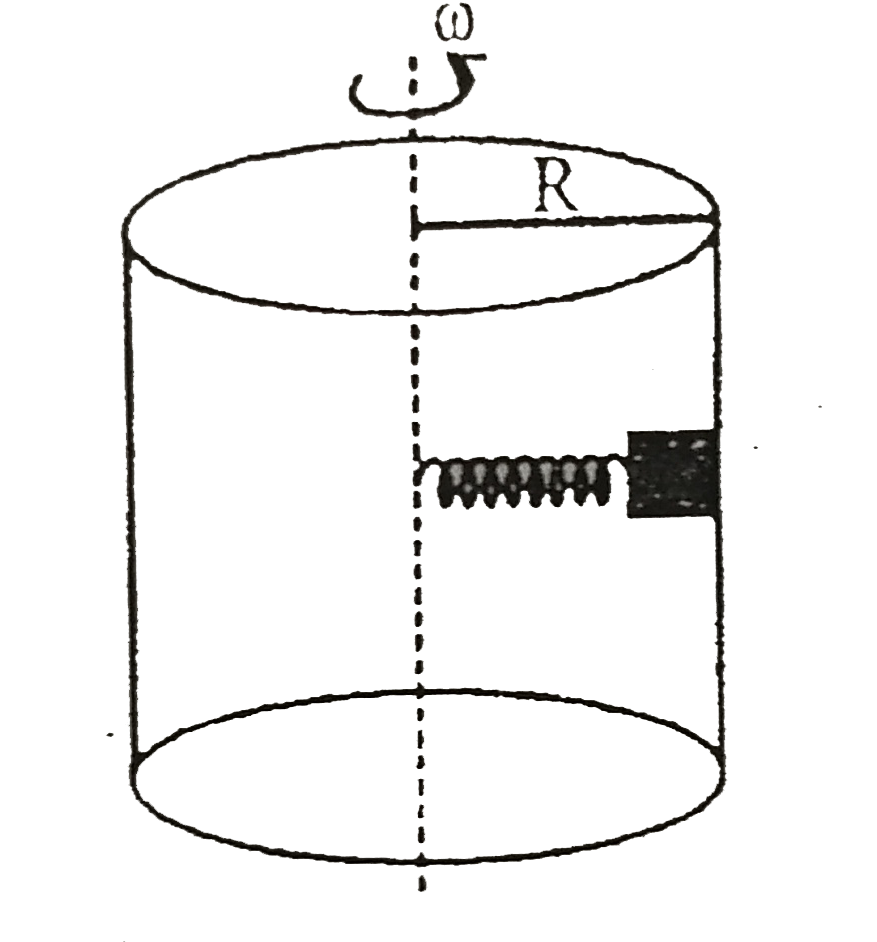
View SolutionOne end of a spring of force constant k is fixed to a vertical wall and the other to a blcok of mass m resting on a smooth horizontal surface. There is another wall at distance x0 from the block. The spring is then compressed by 2x0 and released. The time taken to strike the wall is

View Solution