Question

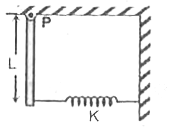
One end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :

Options

A. `2 pi (m//K)^(1//2)`
B. `2 pi sqrt((m(YA + KL))/(YAK))`
C. `2 pi [(m YA//KL)]^(1//2)`
D. `2 pi[(mL//YA)]^(1//2)`

Answer

B

Explanation

Let us consider the wire also as a spring. Then the case becomes two springs attached in series. The equivalent spring constant is
`(1)/(K_(eq))=(1)/(K)+(1)/(K')`
where `K'` is the spring constant of the wire
`:. K_(eq)=(KK')/(K+K')`
Now, `Y=(F//A)/(DeltaL//L)=(F)/(A) xx(L)/(Delta L)`
`(F)/(Delta L)=(YA)/(L)=K'`
We know that time period of the system
`T =2pi sqrt((m)/(K_(eq))) =2pi sqrt((m(K+K'))/(KK'))`
`rArr T=2pi sqrt((m)/(K)[(K+YA//L)/(YA//L)])`
=`2pi sqrt((m(KL+YA))/(KYA))`.