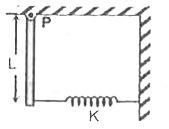
One end of a long metallic wire of length (L) is tied to the ceiling. The other end is tied to a massless spring of spring constant . (K.A) mass (m) hangs freely from the free end of the spring. The area of cross- section and the Young's modulus of the wire are (A) and (Y) respectively. If the mass is slightly pulled down and released, it will oscillate with a time period (T) equal to :
Let the mass m be pulled downwards through distance y. Let the extension in wire of length L be y2 and in spring be y1, figure, then,
y=y1+y2 …(i)
Since there is no mass between spring and wire, the restoring force in the spring and wire will be the same say F.
For a spring, according to Hooke's law,
F=ky1ory1=F/k
For wire, by definitino of Young's modulus,
y=FLAy2ory2=FLAY
Putting values in (i), we get
y=Fk+FYAY=F[AY+kLAYk]
or F=AYkAY+kL]y
As F∝y and it is directed towards the mean position beign restoring force, hence when mass is left free after pulling will execute linear SHM
Here, spring factor =YkAY+kL and
inertia factor = mass of body = m
∴T=2π√inertiafactorspringfactor
=2π√m(AY+kL)AYk

Topper's Solved these Questions
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Multiple Choice Question-I
Explore 21 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Multiple Choice Question-II
Explore 14 Videos
- OSCILLATIONS AND WAVESBook:PRADEEPChapter:OSCILLATIONS AND WAVESExercise:Fill In The Blanks
Explore 20 Videos
- MATHEMATICAL TOOLSBook:PRADEEPChapter:MATHEMATICAL TOOLSExercise:Fill in the blanks
Explore 5 Videos
- PHYSICAL WORLD AND MEASUREMENTBook:PRADEEPChapter:PHYSICAL WORLD AND MEASUREMENTExercise:Competiton Focus Jee Medical Entrance
Explore 18 Videos
Similar Questions
An object of mass m is suspended at the end of a massless wire of length L and area of cross -section A. Young modulus of the material of the wire is Y. If the mass is pulled down slightly its frequency of oscillation along the vertical direction is :
View SolutionA straight rod of light L and mass m is pivoted freely from a point of the roof. Its lower end is connected to an ideal spring of spring constant K. The other end of the spring is connected to the wall as shown in the figure. Find the frequency of small oscillation of the system.
View Solution
Knowledge Check
One end of a long mettalic wire of length L is tied to the ceiling. The other end is tied to massless spring of spring constant K. A mass M hangs freely from the free end of the spring. The area of cross-section and Young's modulus of the wire are A and Y respectively. If the mass is slightly pulled down and released, it will oscillate with a time period T equal to
A2π√(M/K)B2π√M(YA+KL)/YAKC2π√(MYA/KL)D√(ML/YA)A metal wire of length L, area of cross-section A and Young's modulus Y behaves as a spring of spring constant k.
Ak=YA/LBk=2YA/LCk=YA/2LDk=YL/AIf a metal wire of length L, having area of cross-section A and young' s modulus Y . Behave as a spring of spring constant K. The value of K is
AYALBYA2LC2YALDYLA
If a metal wire of length L, having area of cross-section A and Young's modulus Y, behaves as a spring constant K. The value of K is
View SolutionA block of mass M is suspended from a wire of length L, area of cross-section A and Young's modulus Y. The elastic potential energy stored in the wire is
View SolutionA uniform wire of mass m, length L, area of cross-section A and Young's modulus Y hange from the ceiling. Its elongation under its own weight will be
View SolutionA mass (m) is suspended at the end of a weightless wire of length L, cross-sectional area A and Young's modulus Y. The period of oscillation for the S.H.M. along the vertical direction is
View SolutionA mass (m) is suspended at the end of a weightless wire of length L, cross-sectional area A and Young's modulus Y. The period of oscillation for the S.H.M. along the vertical direction is,
View Solution