One end of a uniform glass capillary tube of radius r = 0.025 cm is immersed vertically in water to a depth h = 1cm. The excess pressure (in Nm−2) required to blow an air bubble out of the tube (Given , surface tension of water =7×10−2Nm−1, density of water =10−3kgm−3 and acceleration due to gravity =10ms−2)
0.0048×105
0.0066×105
1.0048×105
1.0066×105
The correct Answer is:B
Excess pressure, p=hdg+h'dg=dg(h+h')
where, h is capillary rise =2Srdg=2×7×10−225×10−5×103×10
= 0.056 m
∴p=103×10[0.056+0.01]
=0.066×104=0.0066×105Nm−2
Topper's Solved these Questions
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - MHT CET Corner
15 Videos
- SURFACE TENSION BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - SURFACE TENSION EXERCISE - Exercise 1
30 Videos
- STATIONARY WAVES BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - STATIONARY WAVES EXERCISE - MHT CET Corner
28 Videos
- WAVE MOTIONBOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - WAVE MOTIONEXERCISE - MHT CET CORNER
23 Videos
Similar Questions
(i) One end of a uniform glass capillary tube of radius r=0.025 cm is immersed vertically in water to a depth h=1cm. Contact angle is 0∘, surface tension of water is 7.5×10–2N/m, density of water is ρ=103kg/m3 and atmospheric pressure is Po=105N/m2
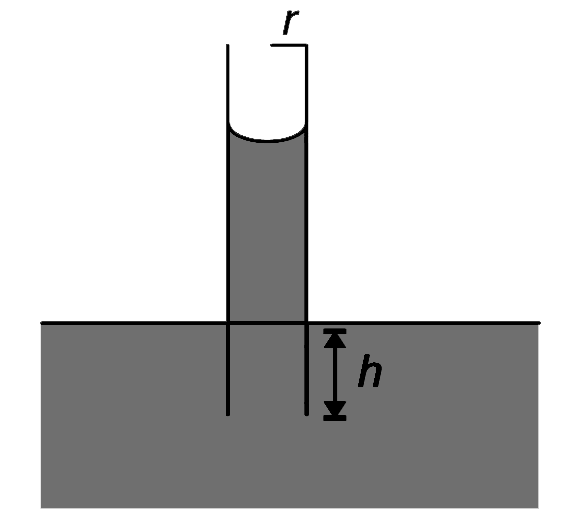
Find the excess pressure to be applied on the water in the capillary tube so that -
(a) The water level in the tube becomes same as that in the vessel.
(b) Is it possible to blow out an air bubble out of the tube by increasing the pressure? (ii) A container contains two immiscible liquids of density ρ1 and ρ2(ρ2>ρ1). A capillary of radius r is inserted in the liquid so that its bottom reaches up to denser liquid and lighter liquid does not enter into the capillary. Denser liquid rises in capillary and attain height equal to h which is also equal to column length of lighter liquid. Assuming zero contact angle find surface tension of the heavier liquid.
View SolutionA glass capillary tube of internal radius r=0.25mm is immersed in water. The top end of the tube projects by 2cm above the surface of water. At what angle does the liquid meet the tube? Surface tension of water =0.7Nm−1.
View Solution
Knowledge Check
One end of a glass capillary tube with a radius r=0.05cm is immersed into water to a depth of h=2cm.Excess pressure required to blow an air bubble out of the lower end of the tube will be (S.T of water =70dyne/cm).Take g=980cm/s2.
A2840dyne/cm2B5840dyne/cm2C7840dyne/cm2D4760dyne/cm2The pressure inside an air bubble of radius 2 cm formed 20 cm below an open water surface is (Given surface tension of water = 70×10−3Nm−1)
A0.3×105Nm−2B0.2×105Nm−2C2.03×105Nm−2D1.03×105Nm−2One end of a glass capillary tube with a radius r is immersed into water to a depth of h The surface tension of water is s and atmospheric pressure is p0 . What pressure is required to blow an air bubble out of the lower end of the tube? Density of water is ρ
AP0−ρgh+2srBP0+ρgh+2srCP0+ρgh−2srDP0−ρgh−2sr
A capillary tube of radius 0.50 mm is dipped vertically in a pot of water. Find the difference between the pressure of the water in the tube 5.0 cm below the surface and the atmospheric pressure. Surface tension of water =0.075Nm−1
View SolutionA glass capillary tube of internal radius r=0.25mm is immersed in water. The top end of the tube projects by 2cm above the surface of water. At what angle does the liquid meet the tube? Surface tension of water =0.7Nm−1.
View SolutionA capillary tube of radius 0.25 mm is submerged vertically in water so that 25 mm of its length is outside water. The radius of curvature of the meniscus will be
(surface tension of water =75×10−3 N/m)
View SolutionAn air bubble of radius 1 mm is located at a depth of 20 cm below water level. The excess pressure inside the bubble above the atmospheric pressure is [Given, the surface tension of water is 0.075 Nm−1 and density is 1000 kg m−3]
View SolutionAn air bubble of radius 1mm is formed inside water at a depth 10m below free surface (where air pressure is 105Nm2). The pressure inside the bubble is – (Surface tension of water = 7x×10–2N/m)
View Solution
