One junction of a certain thermoelectric couple is at a fixed temperature r T and the other junction is at temperature T . The thermo electromotive force for this is expressed by E=K(T−Tr)[T0−12(T+Tr)]. At temperature T=12T0, the thermoelectric power is
12KT0
KT0
12KT20
12K(T0−Tr)2
The correct Answer is:A
Step by step video, text & image solution for One junction of a certain thermoelectric couple is at a fixed temperature r T and the other junction is at temperature T . The thermo electromotive force for this is expressed by E=K(T-T_(r ))[T_(0)-(1)/(2)(T+T_(r ))]. At temperature T=(1)/(2)T_(0), the thermoelectric power is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- HEATING AND CHEMICAL EFFECT OF CURRENTBOOK - ERRORLESS CHAPTER - HEATING AND CHEMICAL EFFECT OF CURRENTEXERCISE - Heating Effect of Current
2 Videos
- HEATING AND CHEMICAL EFFECT OF CURRENTBOOK - ERRORLESS CHAPTER - HEATING AND CHEMICAL EFFECT OF CURRENTEXERCISE - Chemical Effect Current
1 Videos
- ELECTROSTATICS BOOK - ERRORLESS CHAPTER - ELECTROSTATICS EXERCISE - Ordinary Thinking Objective Questions (Electric Flux and Gauss.s Law)
28 Videos
- KINETIC THEORY OF GASESBOOK - ERRORLESS CHAPTER - KINETIC THEORY OF GASESEXERCISE - QUESTIONS
126 Videos
Similar Questions
Knowledge Check
One junction of a certain thermoelectric couple is at a fixed temperature Tr and the other junction is at temperature T. The thermo-electromotive force for this is expressed by E=k(T−Tr)[T0−(12)(T+Tr)]. At temperature T=12T0, the thermoelectric power is
A12kT0BkT0C12kT20D12k(T0−Yr)2One junction of a certain thermoelectric couple is at a fixed temperature Tr and the other junction is at temperature T. The thermo-electromotive force for this is expressed by E=k(T−Tr)[T0−(12)(T+Tr)]. At temperature T=12T0, the thermoelectric power is
A12kT0BkT0C12kT20D12k(T0−Yr)2If for a thermocouple Tn) is the neutral temperature, Tc is the tempreture of the cold junction and Ti) is the temperature of inversion, then
ATi=2Tn−TcBTi=Tn−2TcCTi=Tn−TcDNone of these
The thermo emf E of a thermocouple is found to vary wit temperature T of the junction (cold junction is 0∘C) as
E=40T−T220
The temperature of inversion for the thermocouple is
View SolutionIf the cold junction of thermocouple is kept at 0∘C and the hot junction is kept at T∘C, then the relation between neutral temperature (Tn) and temperature of inversion (Ti) is
View SolutionIf the cold junction of thermocouple is kept at 0∘C and the hot junction is kept at T∘C, then the relation between neutral temperature (Tn) and temperature of inversion (Ti) is
View SolutionThe temperature of the cold junction of the thermocouple is ^(∘)C and the temperature of the hot junction is T∘C. The relation for the thermo emf is given by, E=AT=12BT2 ltbRgt (when A=16 and B=0.08). The temperature of inversion will be
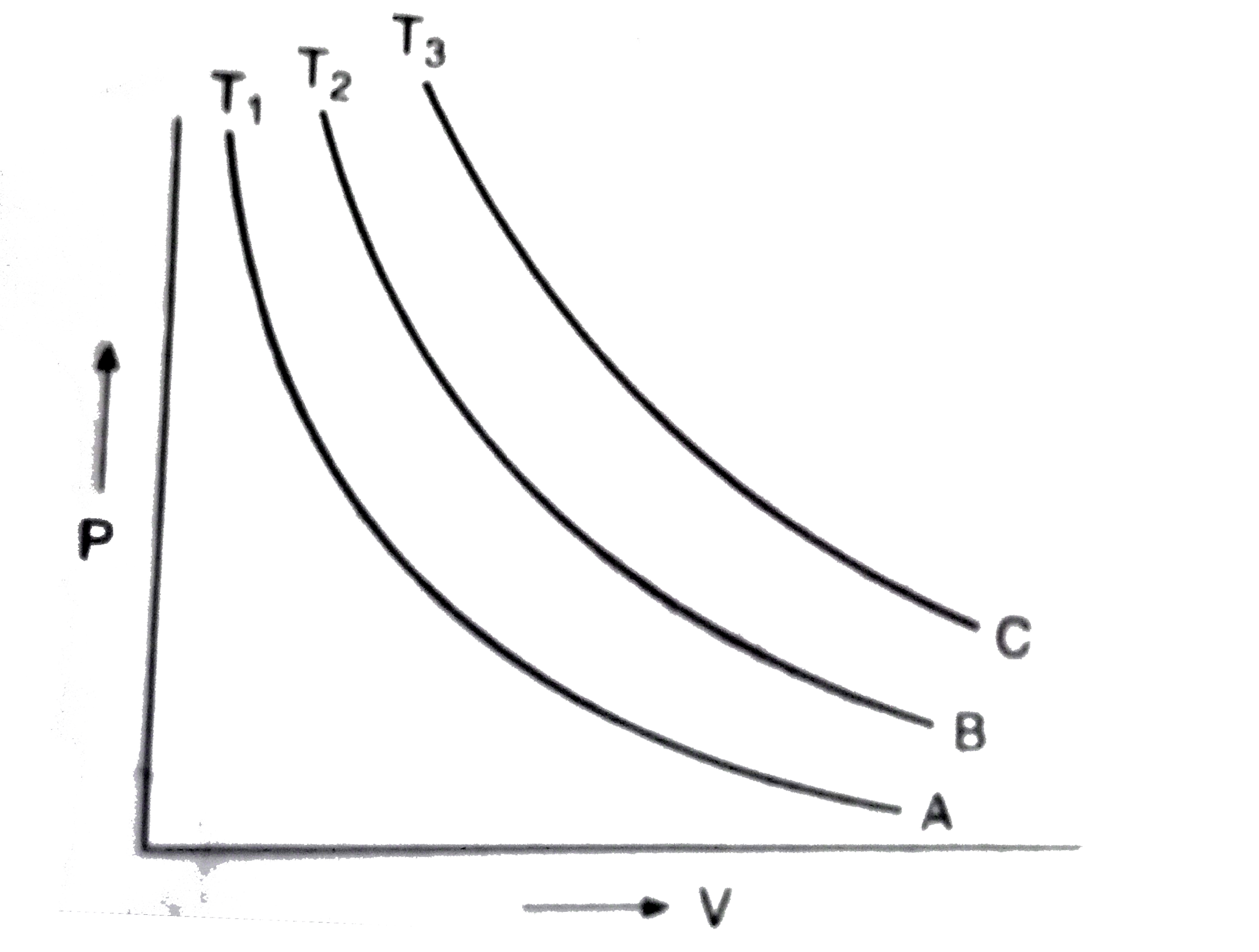
View SolutionIn following isothermal graphs A, B and C at temperatures T1,T2 and T3, the correct order of temperatures will be :
View Solution