One metre long metallic wire is broken into two unequal parts P and Q. The part P is uniformly extended into another wire R. Find the ratio of the resistances of P and R and also the ratio of the lengths P and Q.
To solve the problem step by step, we can break it down as follows:
Step 1: Define the lengths of the parts
Let the length of part P be LP and the length of part Q be LQ. According to the problem, the total length of the wire is 1 meter:
LP+LQ=1 meter
Step 2: Express the length of wire R
The part P is uniformly extended into another wire R. If P is extended uniformly, the length of wire R will be:
LR=2LP
This is because the wire is extended to double its original length.
Step 3: Relate the resistances of P and R
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
For wire P:
RP=ρLPAP
For wire R:
RR=ρLRAR=ρ(2LP)AR
Step 4: Relate the areas of cross-section
Since the volume of wire P before extension is equal to the volume of wire R after extension, we have:
LP⋅AP=LR⋅AR
Substituting LR=2LP:
LP⋅AP=2LP⋅AR
Dividing both sides by LP (assuming LP≠0):
AP=2AR
Step 5: Substitute the area into the resistance formula
Now, substituting AP=2AR into the resistance of P:
RP=ρLP2AR
And for R:
RR=ρ(2LP)AR
Step 6: Find the ratio of resistances
Now we can find the ratio of the resistances RP and RR:
RPRR=ρLP2ARρ(2LP)AR=LP2LP=12
Thus, the ratio of the resistances RP:RR=1:2.
Step 7: Find the ratio of lengths P and Q
From the earlier equation LP+LQ=1, we can express LQ:
LQ=1−LP
Now, using the ratio of resistances:
RPRQ=LPLQ
Since RQ can be expressed in terms of RP and the ratio is 1:2:
RPRQ=12⟹LPLQ=12
Let LP=x and LQ=2x. Then:
x+2x=1⟹3x=1⟹x=13
Thus:
LP=13 meter,LQ=23 meter
Final Ratios
- The ratio of the resistances RP:RR=1:2
- The ratio of the lengths LP:LQ=1:2
Let the length of part P be LP and the length of part Q be LQ. According to the problem, the total length of the wire is 1 meter:
LP+LQ=1 meter
The part P is uniformly extended into another wire R. If P is extended uniformly, the length of wire R will be:
LR=2LP
This is because the wire is extended to double its original length.
The resistance R of a wire is given by the formula:
R=ρLA
where ρ is the resistivity, L is the length, and A is the cross-sectional area.
RP=ρLPAP
RR=ρLRAR=ρ(2LP)AR
Since the volume of wire P before extension is equal to the volume of wire R after extension, we have:
LP⋅AP=LR⋅AR
Substituting LR=2LP:
LP⋅AP=2LP⋅AR
Dividing both sides by LP (assuming LP≠0):
AP=2AR
Now, substituting AP=2AR into the resistance of P:
RP=ρLP2AR
And for R:
RR=ρ(2LP)AR
Now we can find the ratio of the resistances RP and RR:
RPRR=ρLP2ARρ(2LP)AR=LP2LP=12
Thus, the ratio of the resistances RP:RR=1:2.
From the earlier equation LP+LQ=1, we can express LQ:
LQ=1−LP
Now, using the ratio of resistances:
RPRQ=LPLQ
Since RQ can be expressed in terms of RP and the ratio is 1:2:
RPRQ=12⟹LPLQ=12
Let LP=x and LQ=2x. Then:
x+2x=1⟹3x=1⟹x=13
Thus:
LP=13 meter,LQ=23 meter
- The ratio of the resistances RP:RR=1:2
- The ratio of the lengths LP:LQ=1:2
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self
101 Videos
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self
101 Videos
- CHEMICAL EFFECT OF CURRENTBOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B
5 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive
61 Videos
Similar Questions
1 meter long metallic wire is broken into two unequal parts PandQP part of the wire in uniformly extended into another wire R. Length of R is twice the length of P and the resistance of R is equal to that of Q. Find the ratio of the resistance P and R and also the ratio of the length PandQ
View SolutionIn comparing the resistance of two cells PandQ with a sides wire bridge, a balance point is obtained when the sliding contact is 30cm from the zero end of the wire. The resistances PandQ are interchanged and the balance is obtained at 120cm from the same emf. Find the ratio of the resistance PandQ and the length of the bridge wire
View Solution
Knowledge Check
With resistances P and Q in the left and right gaps of a metre bridge respectively, the null point divides the wire in the ratio 1 : 2 . If P and Q are increased by 20Ω each, the null point divides the wire in the ratio 3 : 4, then the resistances P and Q are given as :
AP=10Ω,Q=10ΩBP=10Ω,Q=20ΩCP=40Ω,Q=10ΩDP=20Ω,Q=40Ω
The graph of current versus voltage drop across the three resistors P,Q,R is shown above. Find the ratio of their resistances.
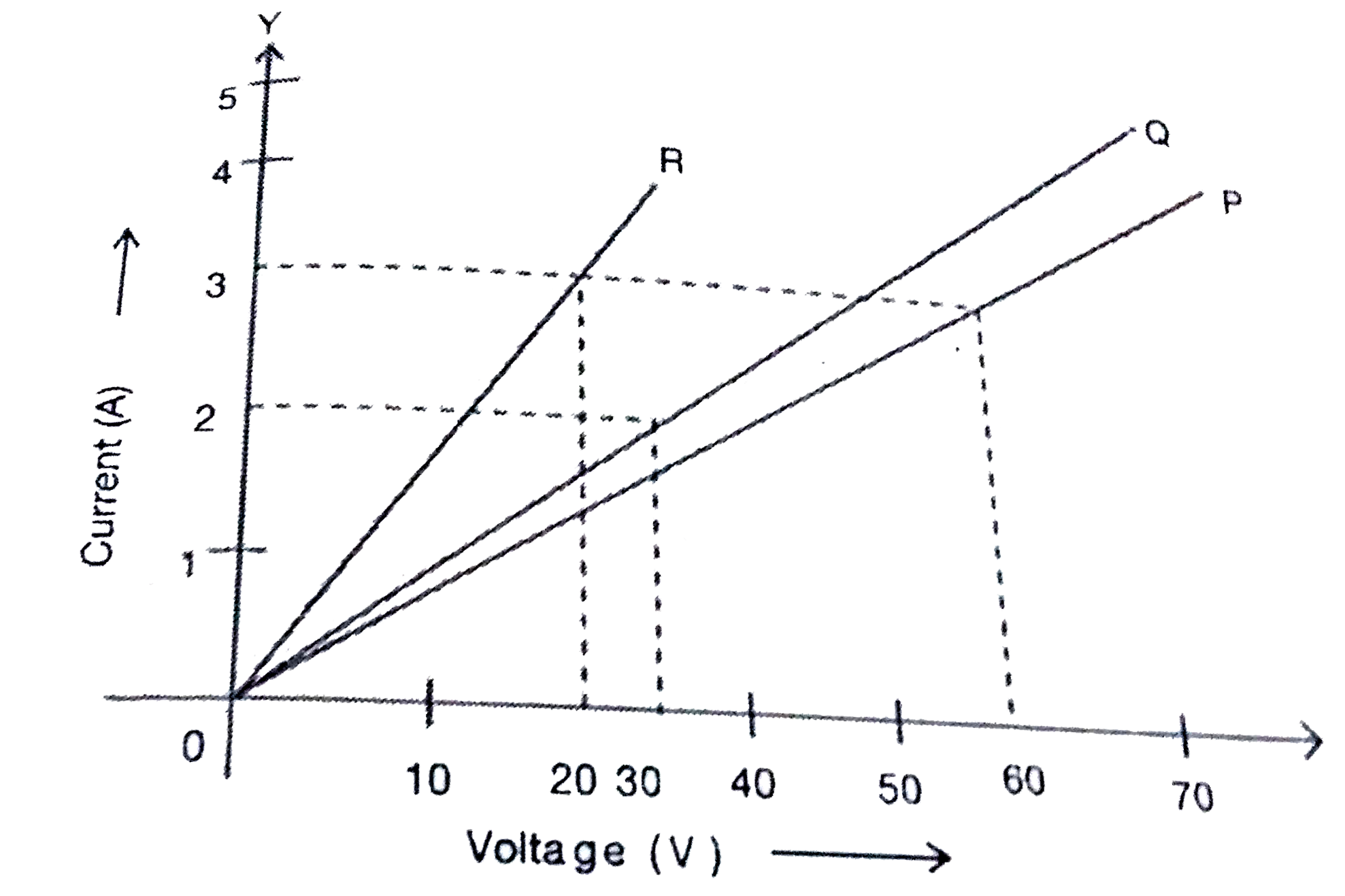
View SolutionA piece of wire of resistance R is cut into five equal parts. These parts are then connected in parallel. If the equivalent resistance of this combination is R', then find the ratio RR'
View SolutionThere is one metal wire of length l, which is broken in two parts of unequal length. One part is called A and the other, B. When the length of A is stretched to double its length then its resistance becomes equal to that of B. What is the original ratio of length of A to that of B?
View SolutionTwo cylinders P and Q of equal mass are made from the same metal. If the radius of P is n times the radius of Q , then calculate ratio of their resistances.
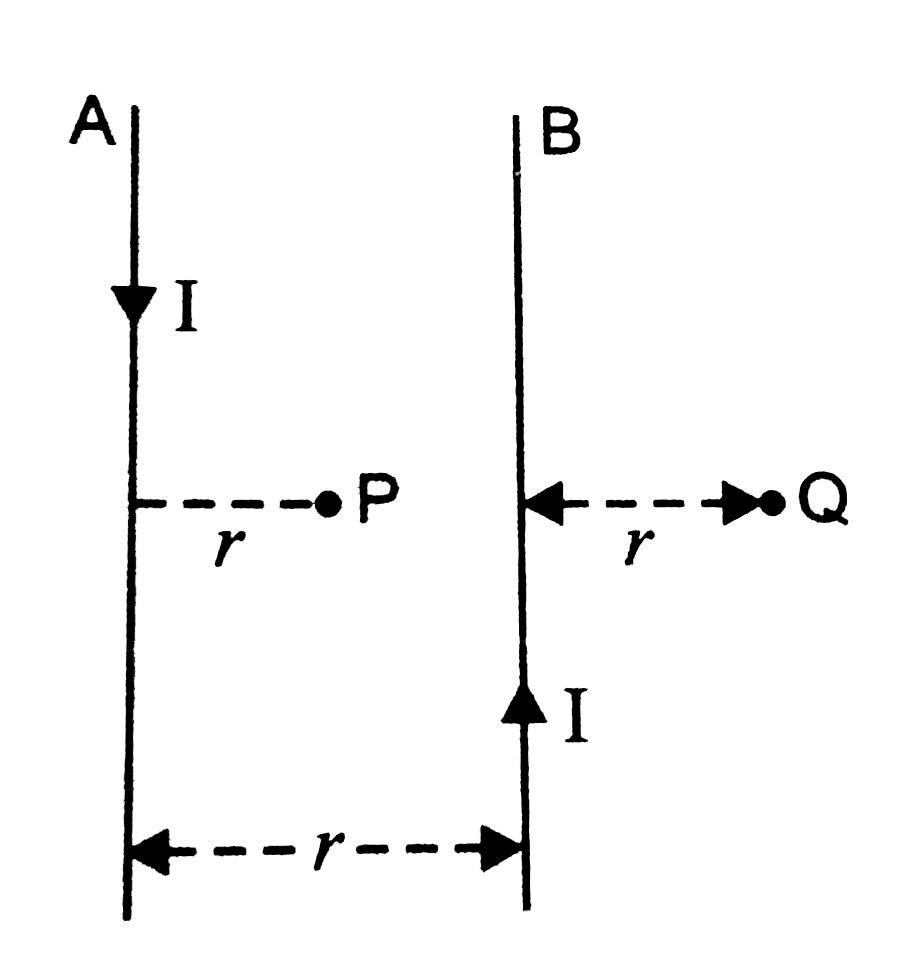
View SolutionThere are two infinite long parallel straight current carrying wires, A and B separated by a distance r. Figure. The current in each wire is I. The ratio of magnitude of magnetic field at point P and Q when points P and Q lie in the plane of wires is:
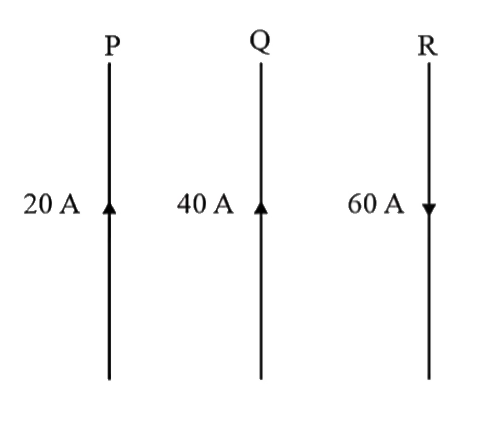
View SolutionP, Q and R are long straight wires in air, carrying currents as shown. The force on Q is directed
View SolutionA certain money is divided among P,Q and R in the ratio 2:7:9 .The total share of P and Q is equal to that of R . Find the difference between P's and Q's share ?
View Solution
