One mole of a mono- atomic ideal gas undergoes a quasi- static process, which is depicted by a straight line joining points (V0T0) and (2V0,3T0) in a V - T diagram . What is the value of the heat capacity of the gas at the point (V0,T0) ?
R
32R
2R
0
The correct Answer is:c
Since path is isochoric .
∴ Work done , dW=PdV Change in internal energy is, ΔU=nCVΔT
where CV = specific heat at constant volume.
Heat given in process is , ΔQ=nCΔT,

where n is number of moles of gas , C is molar heat capacity.
According to graph, temperature is increasing with increase in volume. It means that energy is used both in increasing internal energy and work done.
According to 1st law of thermodynamics
PdV+nCVdT=nCdT
or PndVdT+CV=C .....(i)
At (V0,T0)dVdT=V02T0 ....(ii)
Again , P0V0=nRT0⇒P0n=RT0V0 ....(iii)
From (i), (ii) and (iii) ,
C=RT0V0V02T0+32R=2R[∴ for monoatomic gas , CV=32R]
Topper's Solved these Questions
- THERMODYNAMICSBOOK - MTG-WBJEECHAPTER - THERMODYNAMICSEXERCISE - WB JEE WORKOUT ( CATEGORY 3 : One or Mare than One Option Correct Type (2 Mark )
10 Videos
- SOLID STATE ELECTRONS BOOK - MTG-WBJEECHAPTER - SOLID STATE ELECTRONS EXERCISE - WB JEE Previous Years Questions (CATEGORY 1 : Single Option Correct Type)
15 Videos
- WAVE OPTICSBOOK - MTG-WBJEECHAPTER - WAVE OPTICSEXERCISE - WB JEE PREVIOUS YEARS QUESTION (MCQ.s)
9 Videos
Similar Questions
For two thermodynamic process temperature and volume diagram are given. In first process, it is a straight line having initial and final coordinates as (V0,T0) and (2V0,2T0), where as in second process it is a rectangular hyperbola having intial and final coordinates (V0,T0) and (2V0,T0/2). Then ratio of work doen in the two process must be
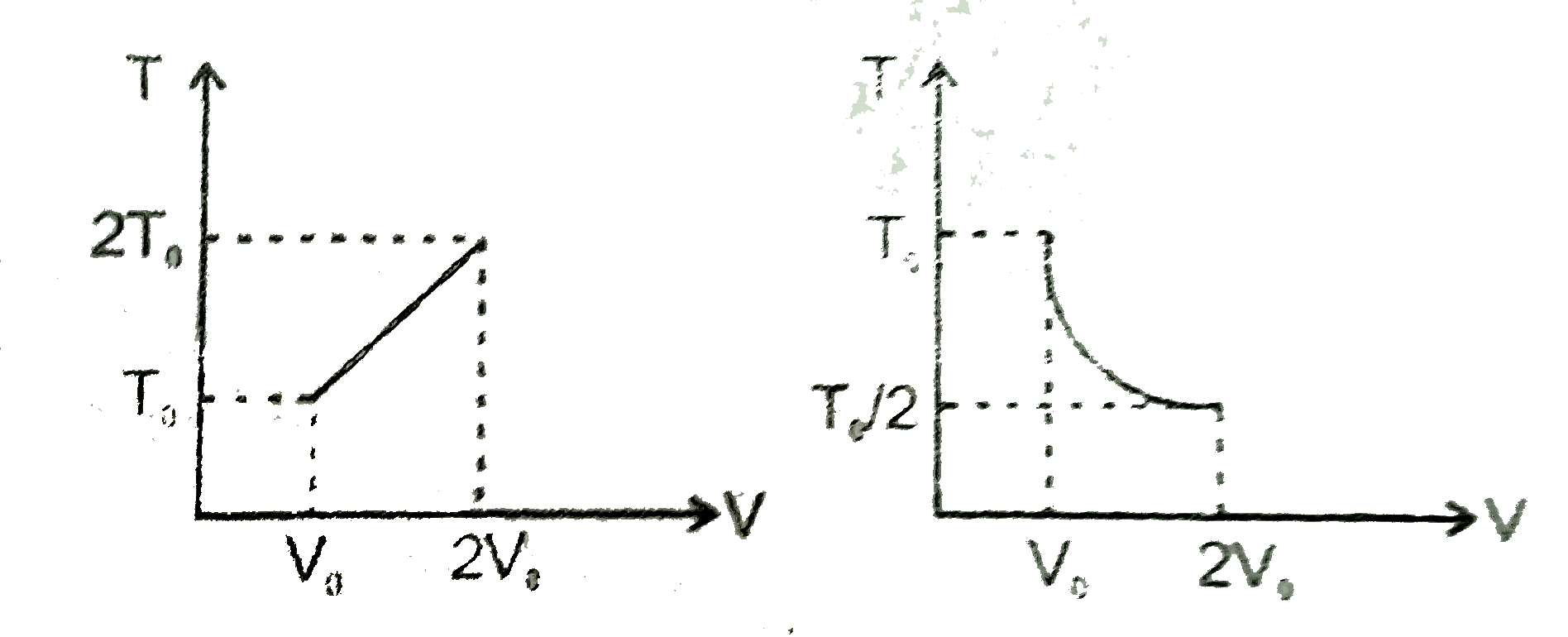
View SolutionFor two thermodynamic process temperature and volume diagram are given. In first process, it is a straight line having initial and final coordinates as (V0,T0) and (2V0,2T0), where as in second process it is a rectangular hyperbola having initial and final coordinates (V0,T0) and (2V0,T0/2). Then ratio of work done in the two process must be

View Solution
Knowledge Check
One mole of monoatomic gas undergoes a process as shown in the P-T diagram below. Choose the corresponding V – T diagram.
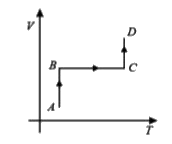 A
A B
B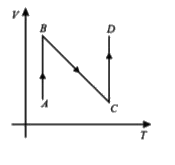 C
C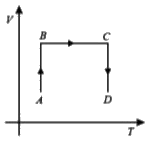 D
D
For two thermodynamic process temperature and volume diagram are given. In first process, it is a straight line having initial and final coordinates as (V0,T0) and (2V0,2T0), where as in second process it is a rectangular hyperbola having intial and final coordinates (V0,T0) and (2V0,T0/2). Then ratio of work doen in the two process must be
 A1:2B2:1C1:1DNone of these
A1:2B2:1C1:1DNone of theseTwo moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The equation of process isA1P=V0T3/204RT52e(T−T0T0)B1P=V0T3/202RT52e(T−T0T0)C1P=V0T3/204RT52e(T+T0T0)D1P=V0T3/203RT52e(T−T0T0)
Two moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The equation of process is
View SolutionTwo moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The minimum volume of gas is
View SolutionOne mole of an ideal gas goes through a process in which the entropy of the gas changes with temperature T as S=aT+CV1nT, where a is a positive constant. CV is the molar heat capacity of this gas at constant volume. Find the volume dependence of the gas temperature in this process if T=T0 at V=V0.
View SolutionOne mole of an ideal monoatomic gas undergoes the process T=T0+4V, where T0 is initial temperature. Find
(i) Heat capacity of gas as function of its volume.
(ii) The amount of heat transferred to gas if its volume increases from V0 to 4V0.
View SolutionTwo moles of an ideal mono-atomic gas undergoes a thermodynamic process in which the molar heat capacity 'C' of the gas depends on absolute temperature as C=RTT0, where R is gas consant and T0 is the initial temperature of the gas. (V0 is the initial of the gas). Then answer the following questions:
The minimum volume of gas is
View Solution
