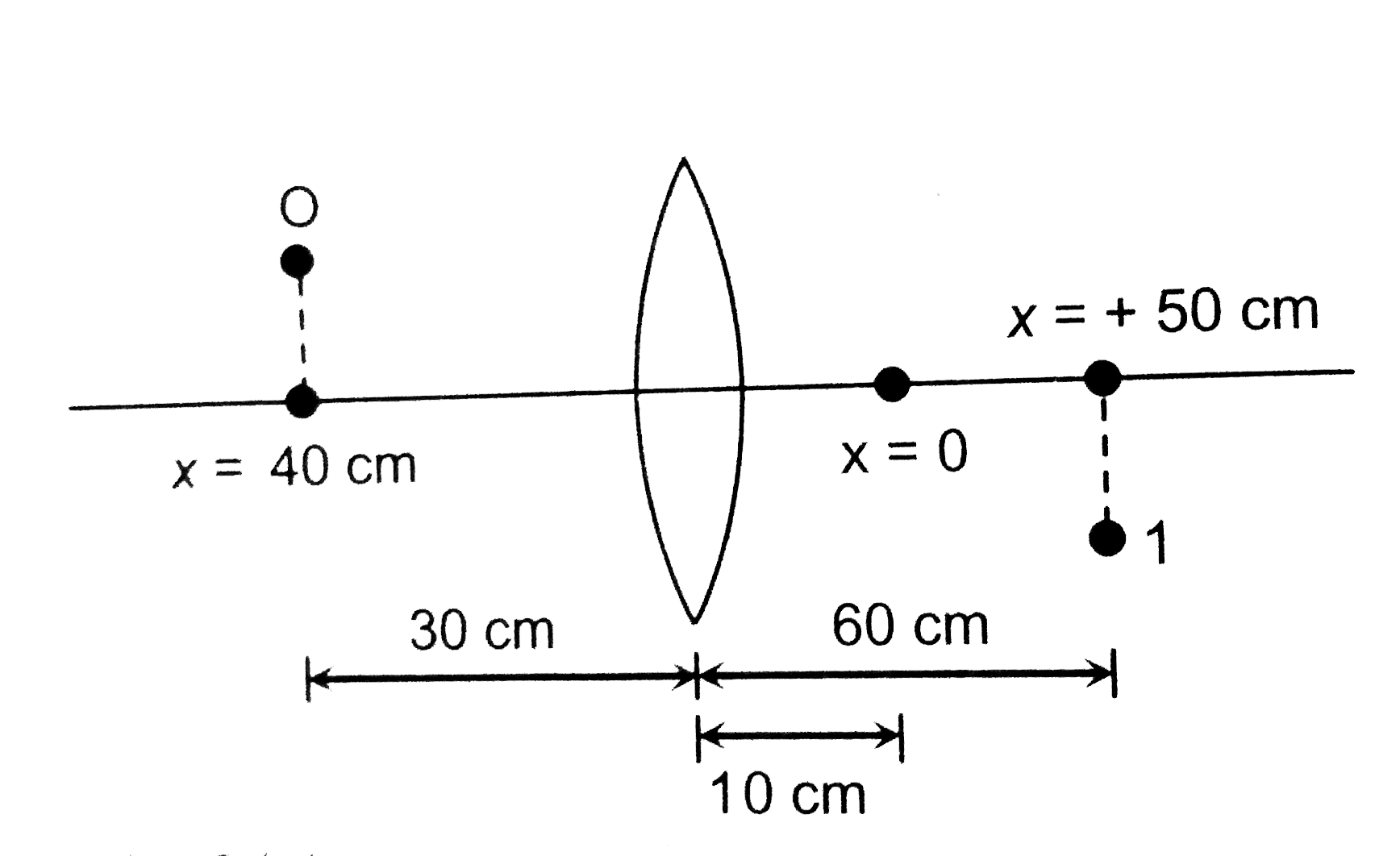
Optic axis of a thin equi-convex lens is the x-axis. The co-ordinates of a point object and its image are (−40cm,1cm)and(50cm,−2cm), respectively. Lens is located at
x=+20cm
x=−30cm
x=−10cm
origin
The correct Answer is:C
Linear magnification m=−2cm1cm=−2
i.e., image is real and inverted.
|v|=2|u|
Let |u|=x then |v|=2x
now |u|+|v|=50−(−40)=90
∴x+2x=90
or x=30cm
Hence, distance of object from the lens is 30cm and of object is 60cm. therefore, lens should be located at x=−10cm as shown in figure.
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Section B - Assertion Reasoning
19 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - AIPMT/NEET Questions
95 Videos
- GEOMETRICAL OPTICSBOOK - A2ZCHAPTER - GEOMETRICAL OPTICSEXERCISE - Optical Instruments
55 Videos
- ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM BOOK - A2ZCHAPTER - ELECTROMAGNETIC WAVES AND COMMUNICATION SYSTEM EXERCISE - Section D - Chapter End Test
30 Videos
- MAGNETISM AND MATTERBOOK - A2ZCHAPTER - MAGNETISM AND MATTEREXERCISE - Section D - Chapter End Test
30 Videos
Similar Questions
Optical axis of a thin equi-convex lens is the x -axis. The co-ordinates of a point object and its image are (10cm,1 cm ) and (100cm,−2cm), respectively.
View SolutionThe principal axis of a thin equi-convex lens is the x-axis. The co-ordinate of a point object and its image are (–20cm,1mm) and (25cm,2mm) respectively. Find the focal length of the lens.
View Solution
Knowledge Check
Optic axis of a thin equiconvex lens is the x-axis. The co-rodinates of a point object and its image axis (−40cm,1cm) and (50cm,−2cm) respectively. Lens is located at
Ax=+20cmBx=−30cmCx=−10cmDoriginWhen an object is moved along the axis is of a lens images three times the size, of the object are obtained when the object is at 16 cm and at 8 cm respectively from the lens. The focal length and nature of the lens are
A12 cm concaveB4 cm concaveC12 cm convexD4 cm convexFor a given optical system, the principal axis is x-axis and coordinates of object are (−30,+1,0) and coordinates of image are (+20,−2,0) All coordinates are in cm.
If the optical system is a convex lens, what is its focal length?A12 cmB10 cmC1003 cmD1009 cm
A point object is located at a distance of 15 cm, from the front surface of a thick bi-convex lens. The lens is 10 cm thick and radii of its front and back surfaces are 10 cm and 25 cm respectively. How fae beyond the back surface of this lens (μ=1.5) is the image formed?
View SolutionA 4 cm tall object is placed on the principal axis of a convex lens. The distance of the object from the optical centre of the lens is 12 cm and its sharp image is formed at a distance of 24 cm from it on a screen on the other side of the lens. if the object if now moved a little away from the lens, in which way (towards the lens or away from the lens) will he have to move the screen to get a sharp image of the object on it again? How will the magnification of the image be affected ?
View SolutionA 4 cm tall object is placed on the principal axis of a convex lens. The distance of the object from the optical centre of the lens is 12 cm and its sharp image is formed at a distance of 24 cm from it on a screen on the other side of the lens. if the object if now moved a little away from the lens, in which way (towards the lens or away from the lens) will he have to move the screen to get a sharp image of the object on it again? How will the magnification of the image be affected ?
View SolutionPlane surface of a thin plano-convex lens is silvered. If a point object is placed on principal axis at a distance 60cm from the lens and fial image is formed at a distance 30cm from the lens on same side. What will be the distance of final imagge from the lens if the plane surface is not silvered.
View SolutionTwo point objects are placed on principal axis of a thin converging lens. One is 20cm from the lens and other is on the other side of lens at a distance of 40 cm from the lens. The images of both objects coincide. The magnitude of focal length of lens is :-
View Solution
