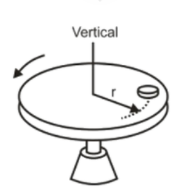
Place a coin on gramophone disc near its centre and set the disc into the rotation. As the speed of rotation increases, the coin will slide away from the centre of the disc. The motion of coin is due to
radial force towards centre
non-conservative force
centrifugal force
centripetal force
The correct Answer is:C
Step by step video, text & image solution for Place a coin on gramophone disc near its centre and set the disc into the rotation. As the speed of rotation increases, the coin will slide away from the centre of the disc. The motion of coin is due to by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - CRITICAL THINKING93videos
CIRCULAR MOTION
- BOOK - TARGET PUBLICATIONCHAPTER - CIRCULAR MOTIONEXERCISE - COMPETITIVE THINKING102videos
CIRCULAR MOTION
- BOOK - TARGET PUBLICATIONCHAPTER - ATOMS, MOLECULES AND NUCLEI EXERCISE - Evaluation test19videos
ATOMS, MOLECULES AND NUCLEI
- BOOK - TARGET PUBLICATIONCHAPTER - CURRENT ELECTRICITY EXERCISE - Evaluation Test6videos
CURRENT ELECTRICITY
Similar Questions
A small coin of mass 40 g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2 rad s−2. The coefficient of static friction between the coin and the disc is μs=3/4 and the coefficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of hte resultant force on the coin exerted by the disc just before it starts slipping on the disc is :
 View Solution
View SolutionA gramophone disc is set revolving in a horizontal plane at the rate of 3312 revolutions per minute. It is found that a small coin placed on the disc will remain there if its centre is not more than 5 cm from the axis of rotation. Calculate the coefficient of friction between the coin and the disc
[Hint : Centripetal force =mω2r= Frictional force =μN=μmg]View Solution
Knowledge Check
- Question 1 - Select One
A circular disc of radius R is removed from a bigger of the discs coincide. The centre of mass of the new disc is ar from the centre of the bigger disc. The value of α is
A14B13C12D16 - Question 2 - Select One
A coin kept on a rotating gramophone disc just beging to slip if its centre is at a distance of 8 cm from the centre of the disc .The angular velocity of the gramophone disc is then doubled , Through what distance , the coin should be shifted towards the centre , so that the coin will just slip ?
A2 cmB4 cmC6 cmD16 cm - Question 3 - Select One
A coins kept on a horizontal rotating disc has its centre at a distance of 0.25 m from the axis of rotation of the disc .If μis0.2, then the angular velocity of the disc at which the coion will slip off, (g=9.8m/s2)
A3.8rad/sB2.8rad/sC4.8rad/sD5.8rad/s
A brass disc is rotating about its axis. If temperature of disc is increased then its
View SolutionA uniform rod of mass m and length L lies radialy on a disc rotating with angular speed ω in a horizontal plane about vertical axis passing thorugh centre of disc. The rod does not slip on the disc and the centre of the rod is at a distance 2L from the centre of the disc. them the kinetic energy of the rod is
 View Solution
View SolutionAssertion: A disc rolls without slipping on a horizontal surface and the linear speed of its centre of mass is v. The rotational speed of the particles on its rim at the top of the disc will be 2v.
Reason: The disc rolls as if it is rotating about the point of contact with the horizontal surface.View SolutionA coin placed on a rotating gramophone disc, remains at rest when it is at a distance of 9 cm from its centre ,the angular velocity of the disc is then tripled .At what distance from the centre ,the coin should be placed , so that it will remain at rest ?
View SolutionA small coin of mass 80g is placed on the horizontal surface of a rotating disc. The disc starts from rest and is given a constant angular acceleration α=2rad/s2. The coefficient of static friction between the coin and the disc is μs=3/4 and cofficient of kinetic friction is μk=0.5. The coin is placed at a distance r=1m from the centre of the disc. The magnitude of the resultant force on the coin exerted by the disc just before it starts slipping on the disc is
 View Solution
View Solution

