Potential energy of the bob is maximum
at the mean position
at the extreme positions
between the mean position and extreme positions
none of these
The correct Answer is:B
To determine when the potential energy of the bob in a simple pendulum is maximum, we can analyze the motion of the pendulum step by step.
1. Understanding the Pendulum Setup:
- A simple pendulum consists of a mass (bob) attached to a string fixed at one end. The bob swings back and forth under the influence of gravity.
2. Identifying Key Positions:
- The mean position (or equilibrium position) is where the bob hangs straight down, and the net force acting on it is zero.
- The extreme positions are the highest points the bob reaches on either side of the mean position during its swing.
3. Potential Energy and Height:
- The potential energy (PE) of the bob is given by the formula:
PE=mgh
where m is the mass of the bob, g is the acceleration due to gravity, and h is the height of the bob above a reference point (usually taken as the mean position).
4. Analyzing Energy at Different Positions:
- At the mean position, the height h is zero, so the potential energy is also zero:
PEmean=mg⋅0=0
- As the bob swings up towards the extreme position, its height h increases, and consequently, its potential energy increases.
5. Maximum Potential Energy:
- At the extreme position, the bob reaches its maximum height h. Therefore, the potential energy is maximum at this point:
PEextreme=mg⋅hmax
- Since h is maximum at the extreme position, the potential energy is also maximum here.
6. Conclusion:
- The potential energy of the bob is maximum at the extreme positions of its swing.
Answer:
The potential energy of the bob is maximum at the extreme position (Option 2).
- A simple pendulum consists of a mass (bob) attached to a string fixed at one end. The bob swings back and forth under the influence of gravity.
- The mean position (or equilibrium position) is where the bob hangs straight down, and the net force acting on it is zero.
- The extreme positions are the highest points the bob reaches on either side of the mean position during its swing.
- The potential energy (PE) of the bob is given by the formula:
PE=mgh
where m is the mass of the bob, g is the acceleration due to gravity, and h is the height of the bob above a reference point (usually taken as the mean position).
- At the mean position, the height h is zero, so the potential energy is also zero:
PEmean=mg⋅0=0
- As the bob swings up towards the extreme position, its height h increases, and consequently, its potential energy increases.
- At the extreme position, the bob reaches its maximum height h. Therefore, the potential energy is maximum at this point:
PEextreme=mg⋅hmax
- Since h is maximum at the extreme position, the potential energy is also maximum here.
- The potential energy of the bob is maximum at the extreme positions of its swing.
The potential energy of the bob is maximum at the extreme position (Option 2).
Topper's Solved these Questions
- WAVE MOTION AND SOUND BOOK - MCGROW HILL PUBLICATIONCHAPTER - WAVE MOTION AND SOUND EXERCISE - HIGH ORDER THINKING QUESTIONS
22 Videos
- SOURCES OF ENERGY BOOK - MCGROW HILL PUBLICATIONCHAPTER - SOURCES OF ENERGY EXERCISE - ELEMENTARY QUESTIONS
82 Videos
- WORK AND ENERGYBOOK - MCGROW HILL PUBLICATIONCHAPTER - WORK AND ENERGYEXERCISE - HIGHER ORDER THINKING QUESTIONS
29 Videos
Similar Questions
Electric dipole is placed in external electric field. When the potential energy of dipole is maximum?
View SolutionDerive an expression for potential energy of an electric dipole in a uniform electric field. In which situation, the potential energy fo dipole is (i) maximum and (ii) minimum.
View Solution
Knowledge Check
In a simple harmonic motion
(i) the maximum potential energy equal the maximum kinetic energy
(ii) the minimum potential energy equals the minimum kinetic energy
(iii) the minimum potential energy equals the maximum kinetic energy
(iv) the maximum potential energy equals the minimum kinetic energyA(i),(ii)B(i),(iii)C(ii),(iii)D(i), (iv)Displacement between maximum potential energy position energy potential and maximum kinetic energy position for a particle executing S.H.M is
A−aB+aC±aD±a4The gravitational potential energy is maximum at :
AinfinityBthe earth's surfaceCThe centre of the earthDTwice the radius of the earth
A bob of mass 2 kg hangs from a string of length 5 m . It swings from its rest position to one of the sides so that the string makes an angle of 60∘ with the vertical Calculate the gain in potential energy of the bob .
View SolutionA pendulum initially is at rest in vertical position. The bob is pulled slowly towards right. Find the change in gravitational potential energy of the pendulum bob of mass m as the function of x.
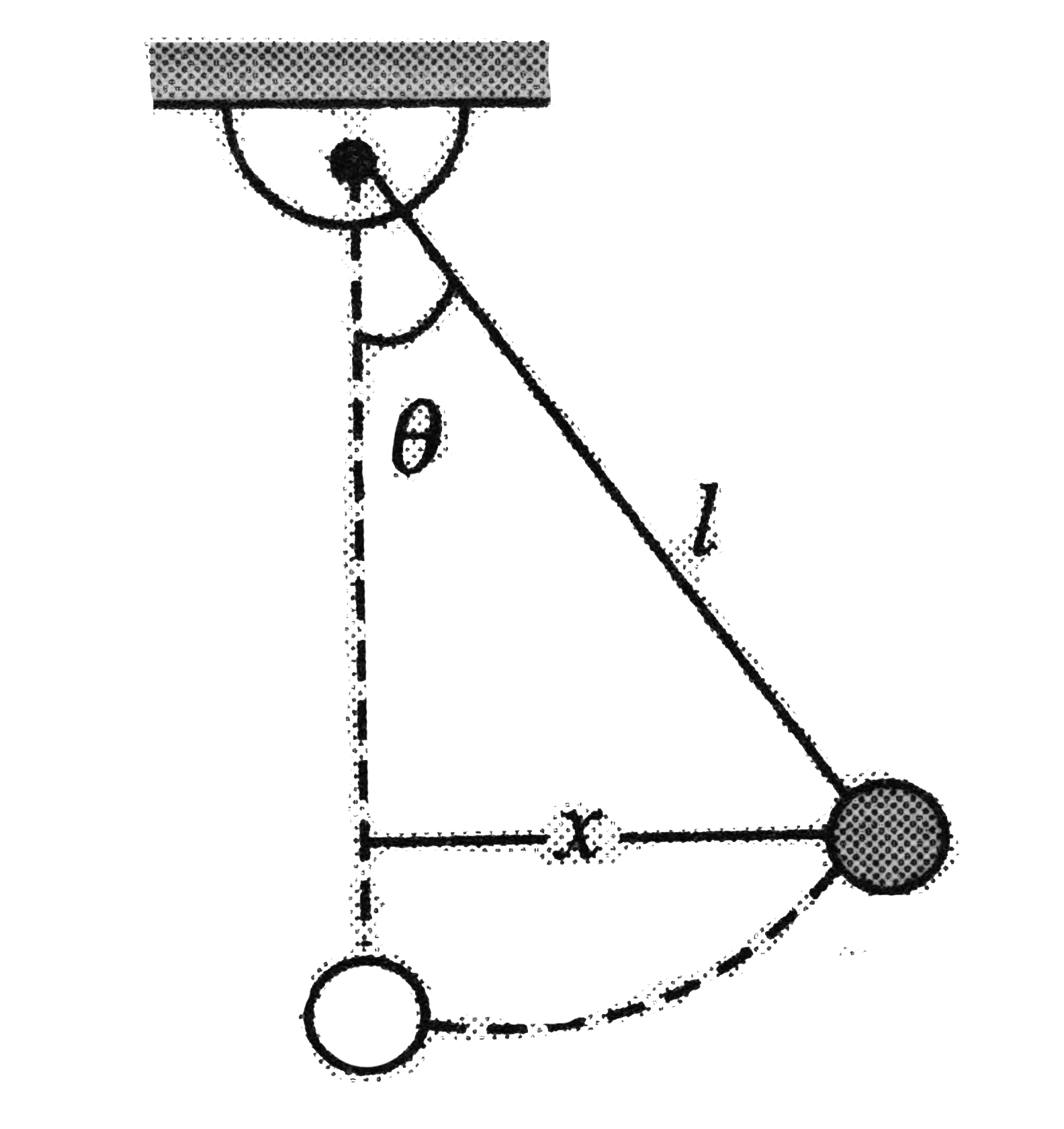
View Solution(a) What is the gravitational potential energy of an object on Earth due to ? (b) At which point in the swing of an ideal simple pendulum (ignoring friction) is the gravitational potential energy the maximum ?
View SolutionPotential energy and potential
View SolutionA simple pendulum of length l has a maximum angular displacement θ. The maximum kinetic energy of the bob of mass m will be
View Solution
