Pressure P, volume V and temperature T for a certain gas are related by P=AT−BT2V, where A and B are constatns .The work done by the gas as its temperature change from T1 to T2 while pressure remaining constatn is
A−B2(R2−T1)
A(T2−T1)−B(T22−T21)
A2(T22−T21)−B3(T32−T31)
A(T2−T1)−B3(T2−T1)3
The correct Answer is:B
To find the work done by the gas as its temperature changes from T1 to T2 while the pressure remains constant, we will follow these steps:
Step 1: Understand the relationship between P, V, and T
Given the equation:
P=AT−BT2V
we can rearrange this to express PV:
PV=AT−BT2
Step 2: Set up the work done equation
The work done dW by the gas during an infinitesimal change in volume dV at constant pressure P is given by:
dW=PdV
Step 3: Differentiate the equation with respect to T
To find dV, we differentiate the equation PV=AT−BT2 with respect to T:
d(PV)dT=d(AT−BT2)dT
Since P is constant, we have:
PdVdT=A−2BT
Thus, we can express dV in terms of dT:
dV=A−2BTPdT
Step 4: Substitute dV into the work equation
Substituting dV into the work done equation:
dW=P(A−2BTPdT)=(A−2BT)dT
Step 5: Integrate to find the total work done
Now, we integrate dW from T1 to T2:
W=∫T2T1(A−2BT)dT
Calculating the integral:
W=(AT−BT2)T2T1
This gives:
W=(AT2−BT22)−(AT1−BT21)
Simplifying this, we get:
W=A(T2−T1)−B(T22−T21)
Final Result
Thus, the work done by the gas as its temperature changes from T1 to T2 while pressure remains constant is:
W=A(T2−T1)−B(T22−T21)
---
Given the equation:
P=AT−BT2V
we can rearrange this to express PV:
PV=AT−BT2
The work done dW by the gas during an infinitesimal change in volume dV at constant pressure P is given by:
dW=PdV
To find dV, we differentiate the equation PV=AT−BT2 with respect to T:
d(PV)dT=d(AT−BT2)dT
Since P is constant, we have:
PdVdT=A−2BT
Thus, we can express dV in terms of dT:
dV=A−2BTPdT
Substituting dV into the work done equation:
dW=P(A−2BTPdT)=(A−2BT)dT
Now, we integrate dW from T1 to T2:
W=∫T2T1(A−2BT)dT
Calculating the integral:
W=(AT−BT2)T2T1
This gives:
W=(AT2−BT22)−(AT1−BT21)
Simplifying this, we get:
W=A(T2−T1)−B(T22−T21)
Thus, the work done by the gas as its temperature changes from T1 to T2 while pressure remains constant is:
W=A(T2−T1)−B(T22−T21)
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - HOTs
8 Videos
- THERMODYNAMICSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - Assertion & Reason
15 Videos
- THERMAL PROPERTIES OF MATTERBOOK - NCERT FINGERTPS ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assertion And Reason
10 Videos
- UNITS AND MEASUREMENTSBOOK - NCERT FINGERTPS ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Assertion And Reason
15 Videos
Similar Questions
Pressure p, volume V and temperature T for a certain gas are related by
p=αT−βT2V
where, α and β are constants. Find the work done by the gas if the temperature changes from T1 to T2 while the pressure remains the constant.
View SolutionPressure P, Volume V and temperature T of a certain material are related by the P=αT2V. Here α is constant. Work done by the material when temparature changes from T0 to 2T0 while pressure remains constant is :
View Solution
Knowledge Check
The temperature of n moles of an ideal gas is increased from T to 4T through a process for which pressure P=aT−1 where a is a constant .Then the work done by the gas is
Aa. nRTBb. 4nRTCc. 2nRTDd. 6nRT
n moles of an ideal gas undergo a process in which the temperature changes with volume as T=kv2. The work done by the gas as the temperature changes from T0 to 4T0 is
View SolutionThe volume V versus temperature T graphs for a certain amount of a perfect gas at two pressure p1andp2 are as shown in Fig. It follows from the graphs that p1 is greater than p2.
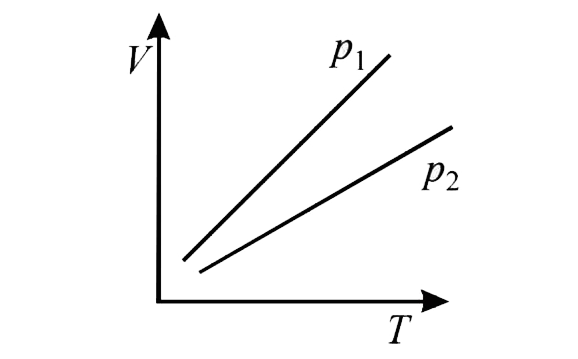
View SolutionThe volume V versus temperature T graphs for a certain amount of a perfect gas at two pressure p1andp2 are as shown in Fig. Show that p1 is less than p2.

View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionOne mole of an ideal gas at temperature T expands slowly according to the law pV= constant.
Its final temperature is T2. The work done by the gas is
View SolutionAn ideal monatomic gas undergoes a process where its pressure is inversely proportional to its temperature.
(a) Calculate the molar specific heat of the process.
(b) Find the work done by two moles of gas if the temperature change from T1 to T2.
View Solution
