Prove that the mid-point of the hypotenuse of right angled triangle is equidistant from its vertices.
Here∠CAB=90∘ let D be the mid -point of hypotenuse,
We have
BD=DC
AB=AD+DB
Ac=AD+DC=AD+BD…(i)
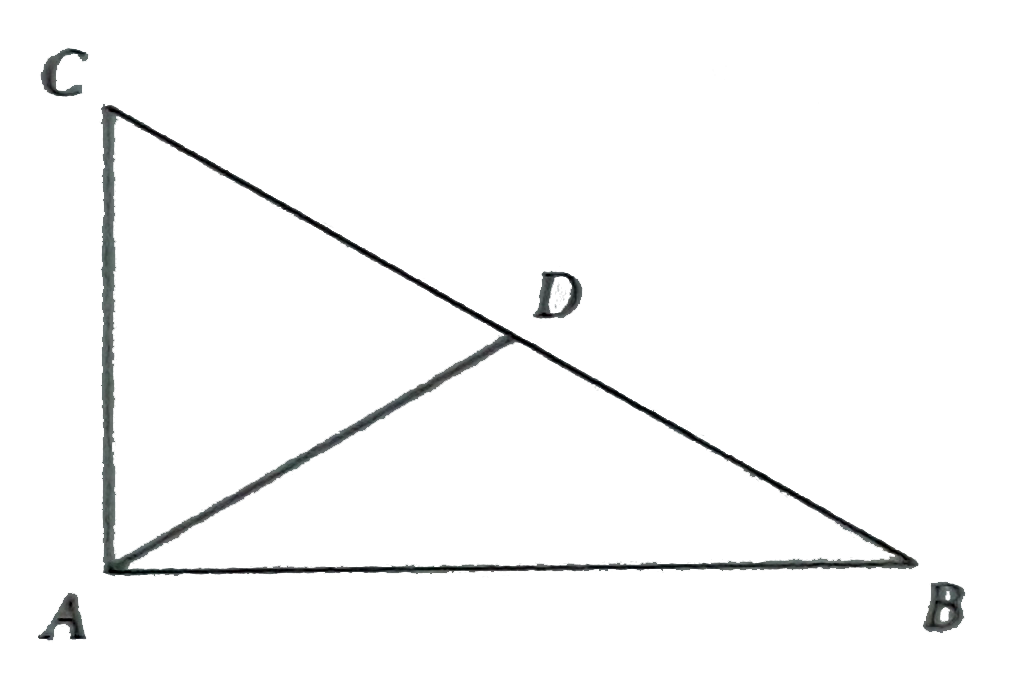
since ,∠BAC=90∘
AB⊥AC
(AD+DB).(AD+BD)=O
(AD−BD).(AD+BD)=O
AD2−BD2=O
∴AD=BDalso,BD=DC
thereforeD is mid-pointof BC.
thus,|AD|=|BD|=|DC|.
Hence ,its proved that the mid -point of the hypotenuse of right angled triangle is equidistant from its vertices.
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the measure of the hypotenuse of a right triangle, when its medians, drawn from the vertices of the acute angles, are 5 cm and 2√10cm
A5√8cmB2√13cmC6√10cmD2√7cm
In Fig. 14.40, a right triangle BOA is given. C is the mid-point of the hypotenuse AB . Show that it is equidistant from the vertices O, A and B . (FIGURE)
View SolutionWhat is the measure of the hypotenuse of a right triangle, when its medians, drawn from the vertices of the acute angles, are 5 cm and 2√10 cm long ?
View SolutionA point on the hypotenuse of a right angled triangle is at distance 8 cm and 1 cm from the other sides of the triangle. Minimum length of hypotenuse is √λ Then value of λ10 is
View SolutionProve that the line segment joining the mid-point of the hypotenuse of a right triangle to its opposite vertex is half of the hypotenuse.
View SolutionProve that the area of the equilateral triangle drawn on the hypotenuse of a right angled triangle is equal to the sum of the areas of the equilateral triangles drawn on the other two sides of the triangle.
View SolutionProve by vector method, that in a right-angled triangle ABC, AB2+AC2=BC2, the angle A being right angled. Also prove that mid-point of the hypotenuse is equidistant from vertex.
View SolutionIf D is the mid-point of the hypotenuse AC of a right triangle ABC, prove that BD=12AC
View Solution
