Prove the relation aμb=1bμa
By the principle of reversibility we know that if a ray of light after suffering a number of reflections or refractions, finally falls normally on a plane mirror then its path is reversed.
Fig shows a ray of light AB refraction at the boundary XY separating the two media, falls normally on the plane mirror M and gets reflected back and retraces its path.
Using Snell.s law for incident ray:
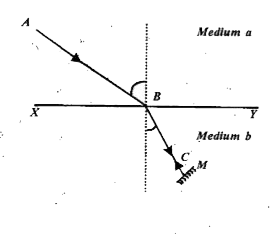
aμb=sinisinr ............1
For reflected ray: bμa=sinrsini.........2
Multiplying 1 and 2 aμb×bμa=1
bμa+1aμb
Topper's Solved these Questions
- REFRACTION OF LIGHTBook:BETTER CHOICE PUBLICATIONChapter:REFRACTION OF LIGHTExercise:LONG ANSWER TYPE QUESTIONS
Explore 9 Videos
- REFRACTION OF LIGHTBook:BETTER CHOICE PUBLICATIONChapter:REFRACTION OF LIGHTExercise:NUMERICAL PROBLEMS
Explore 36 Videos
- REFRACTION OF LIGHTBook:BETTER CHOICE PUBLICATIONChapter:REFRACTION OF LIGHTExercise:MOST EXPECTED QUESTIONS
Explore 2 Videos
- REFLECTION OF LIGHT Book:BETTER CHOICE PUBLICATIONChapter:REFLECTION OF LIGHT Exercise:NUMERICALS PROBLEMS
Explore 7 Videos
- SEMI CONDUCTOR DEVICESBook:BETTER CHOICE PUBLICATIONChapter:SEMI CONDUCTOR DEVICESExercise:Most Expected Questions
Explore 6 Videos
Similar Questions

In the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive
indices of the mediums 1,2,3,4 and 5 respectively. Consider
the following:
(1) μ1=μ2 (2) μ3=μ4=μ5
(3) μ2<μ3 (4) μ4>μ5
Which of the above are correct?
View SolutionConsider the situation as shown in the figure. If μ1 is the friction coefficient between block A and incline and μ2 is the friction coefficient between block B and incline. Find the acceleration of block A if (a) μ1=15,μ2=25 and (b) μ1=25,μ2=15.

View Solution
Knowledge Check
A physical quantity u is given by the relation u=B22μ0
Here B= magnetic field strength
μ0= magnetic permeability of vacuum
The name of physical quantity u isAenergyBenergy densityCpressureDnone of theseA convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
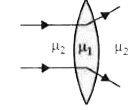 Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2In the figure shown μ1,μ2,μ3,μ4andμ5 are the refractive indices
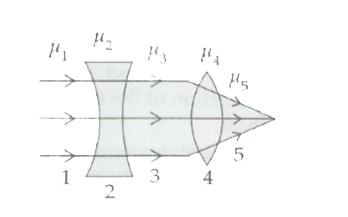
of the mediums 1,2,3,4 and 5 respectively . Consider the following
(1) μ1=μ2 (2) μ3=μ4=μ5
μ2<μ3 (4) μ4>μ5A1 and 2 onlyB1, 2, and 3 onlyC1 and 3 onlyD3 and 4 only
What is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.
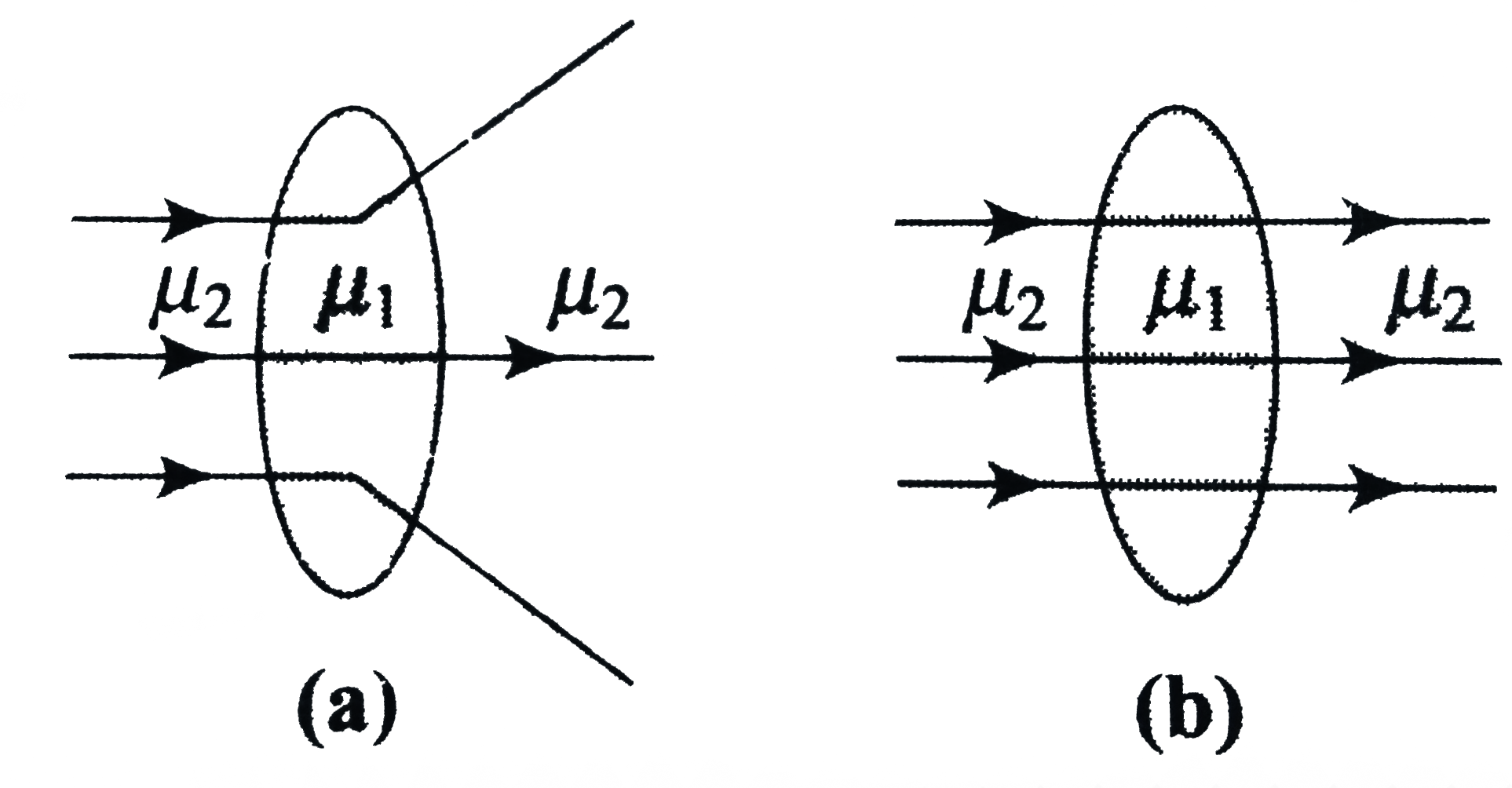
View SolutionWhat is the relation between the refractive indicesμ,μ1 and μ2 if the behaviour of light rays is shown in Figure.

View SolutionTwo transparent media of refractive indices μ1 and μ3 have a solid lens shaped transparent material of refractive index μ2 between them as shown in figures in Columns B. A ray traversing these media is also shown in the figures. In Column A different relationships between μ1,μ2 and μ3 are given. Match them to the ray diagrams shown in Columns B.
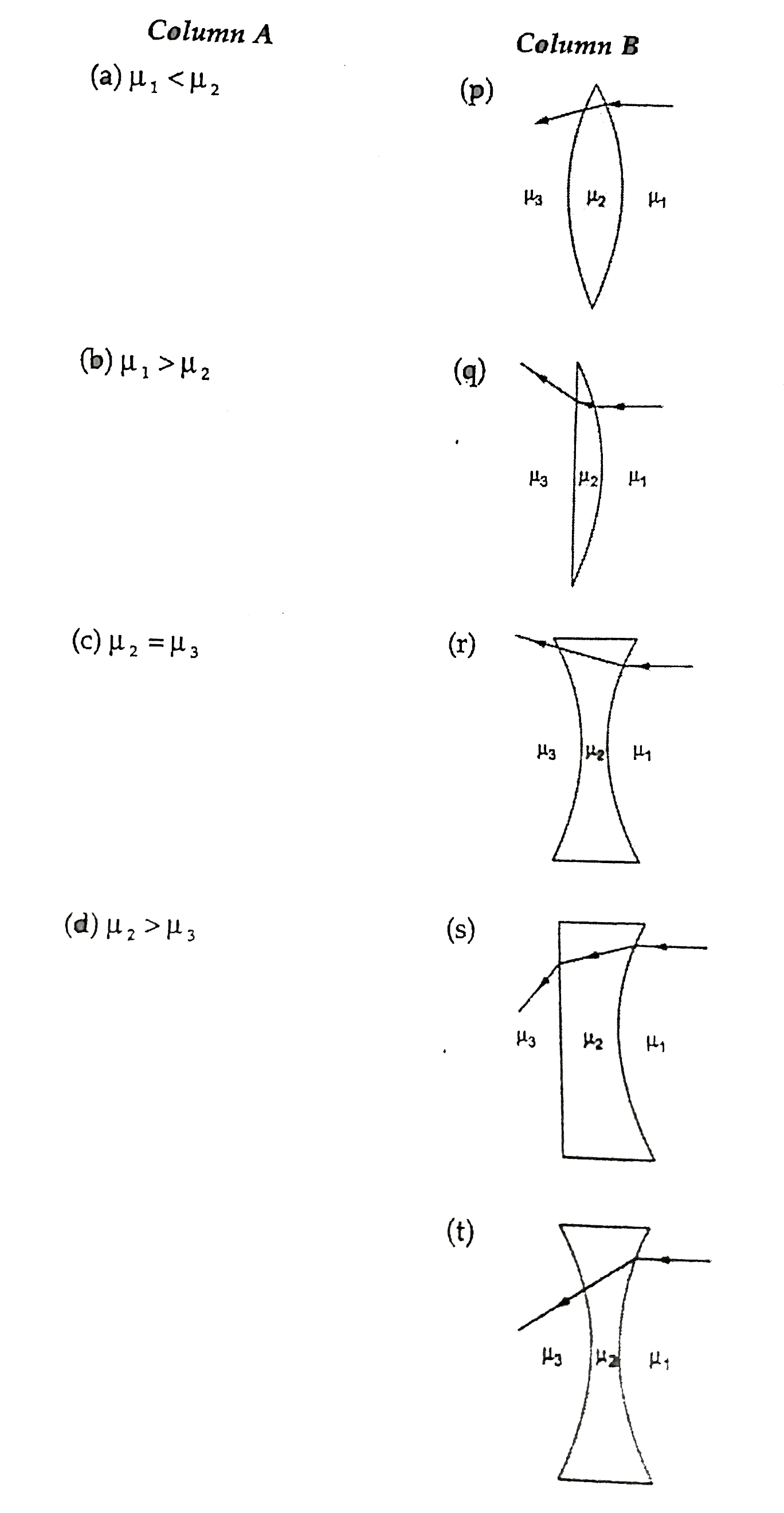
View SolutionIf the magnetic dipole moment of an atom of diamagnetic material , paramagnetic material and ferromagnetic amterial are denote by μd,μpandμf respectively, then:
(a) μp=0andμf≠0
(b) μd=0andμp≠0
(c) μd≠0andμp=0
(d) μd≠0andμp=0
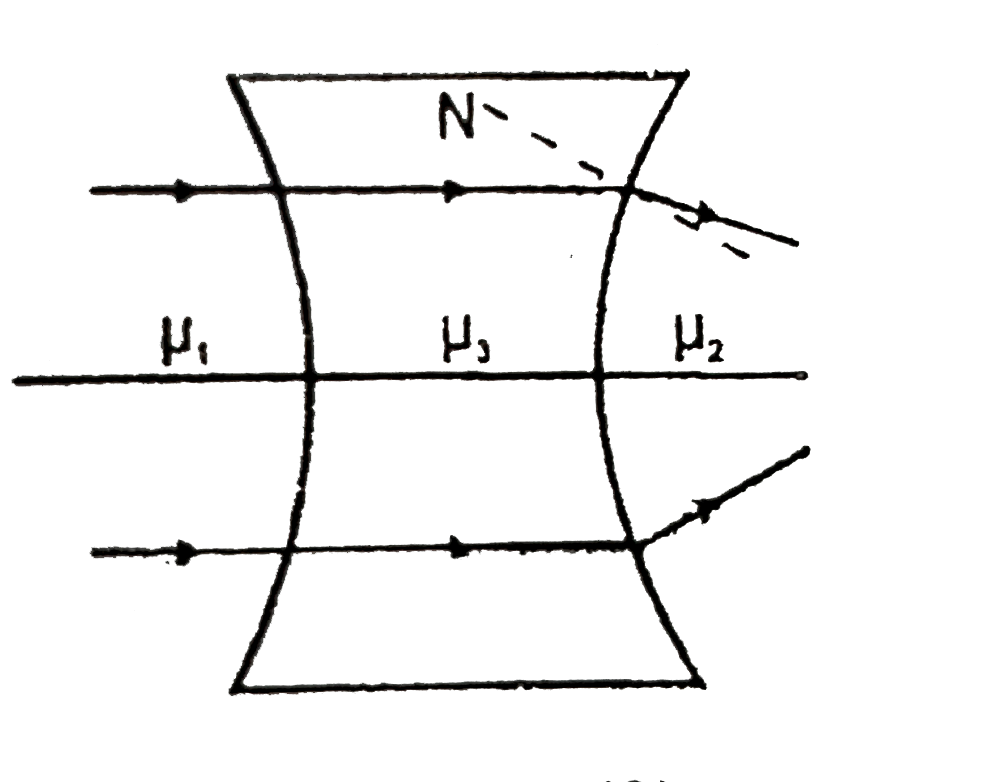
View SolutionFrom the figure shown establish a relation between μ1,μ2,μ3.
View Solution
